VI тарау. Кейіннен болатын жайттың алғышарты туралы

Сыртына шеңбер салынған әрбір төртбұрышта қарама-қарсы қабырғаларының көбейтіндісі, егер оларды қоссақ, осы төртбұрыштың диагональдерінің көбейтіндісіне тең.

ABCD шеңбері ABCD төртбұрышына сырттай сызылған болсын, оның диагональдері -AC мен BD (27-сурет). Мен AB-ның CD-ға және AD-ның BC-ға көбейтінділерінің қосындысы, егер оларды қоссақ, AC-ның BD-ға көбейтіндісіне тең деп тұжырымдаймын.

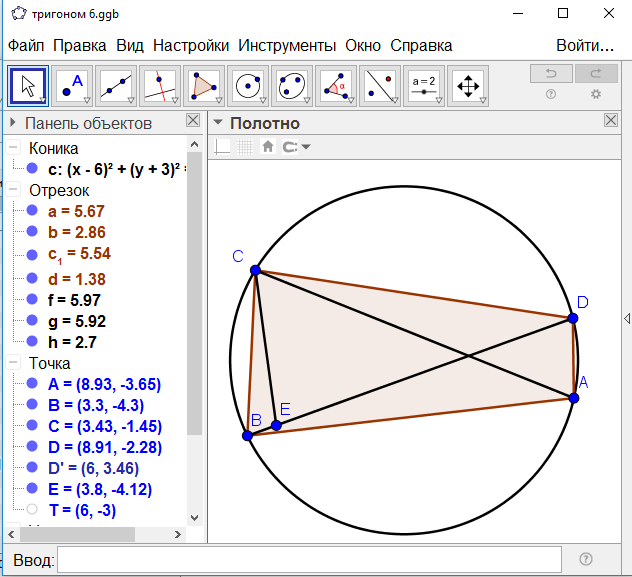
Сурет 27-Шеңбердің хордасының оннан бір және бестен бір бөлігін

табудың келесі әдісі

Осының дәлелдеуі. BCA-ға тең DCE бұрышын саламыз; DCE бұрышы || BCA бұрышына тең, ал АСЕ бұрышы – жалпы болғандықтан, DCA бұрышы BCE бұрышына тең; CADбұрышы CBD бұрышына тең, себебі олар бір CD доғасында орналасқан; демек, қалған ADC бұрышы BEC бұрышына тең. Сондықтан CA-ның AD-ға қатысты болғанындай CBBE-ге қатысты және CB мен AD-ның көбейтіндісі AC мен BE-нің көбейтіндісіне тең.

DCE бұрышы BCA бұрышына тең болғандықтан, ал CDB бұрышы CAВ бұрышына тең болғандықтан, себебі олар бірдей ВС доғасында орналасқан, онда CED бұрышы ABC бұрышына тең, сондықтан CD DE-ге CA-ның AB-ға қатысындай қатысты және CD мен AB-ның көбейтіндісі CA мен DE-нің көбейтіндісіне тең; бірақ CB-ның AD-ға көбейтіндісі CA-ның BE-ге көбейтіндісіне тең екендігі дәлелденген. Осыдан AC-ның BD-ға көбейтіндісі CB-ның AD-ға және CD-ның AB-ға көбейтінділеріне тең. Бұл біздің дәлелдегіміз келгені.