Салудың алгоритмі:

1.  AВС сегментін саламыз да В нүктесінде тең екіге бөлеміз.

2.  AВ және ВС нүктелерін қосамыз.

3.  А және С нүктелерінен ВСD ;және BAD  тік бұрышын тұрғызамыз,

4.  E нүктесі ABC шеңберінің центрі болып табылады.

Сонда E нүктесі ABC⁷ доғасының центрі болып табылады.

Математикалық негіздеу: Тікбұрышты үшбұрышқа сырттай сызылған шеңбердің центрі гипотенузаның  қақ ортасында жатады.

[II] Егер ол центрі D нүктесі болатын ВС дөңгелегіне А нүктесінен қалай жанама жүргізуге болады десе, онда AD сызығын жүргіземіз. Ол ВС дөңгелегін В нүктесінде қияды. D центрінен DА қашықтықта AE дөңгелегін салайық. В нүктесінде АВЕ тік бұрышын тұрғызып, ВС дөңгелегін С нүктесінде қиятын ЕD сызығын жүргіземіз. А мен С - ны қосамыз. Сонда АС ВС⁸ дөңгелегіне жүргізілген жанама болып табылады. Міне оның суреті [34 - сурет].

[34 - сурет]

Салудың алгоритмі:

1.     Центрі D нүктесі болатын ВС дөңгелегіне А нүктесінен жанама жүргізу үшін AD кесіндісін жүргіземіз.

2.      AD кесіндісі ВС дөңгелегін В нүктесінде қияды. D центрі арқылы радиусы AD болатындай AE дөңгелегін сызамыз.

3.     В нүктесі арқылы АВЕ тік бұрышын тұрғызып, ВС дөңгелегін С нүктесі арқылы кесетін ЕD кесіндісін жүргіземіз.

4.      А және С нүктелерін қосамыз.

Сонда АС кесіндісі ВС дөңгелегіне жүргізілген жанама болады.

Математикалық негіздеу: Шеңберге жүргізілген жанама радиусқа перпендикуляр болады.

[IIІ] Егер ол жанаманы қолөнершінің тәсілі бойынша сал десе, онда сызғышты ВС сызығына орналастырып циркульді бір шамаға ашамыз. Егер оның бір ұшы сызғыш бойымен қозғалатын болса, онда екінші ұшы А нүктесі арқылы өтіп, ВС⁹-ға параллель сызықты береді. Міне оның суреті [35 - сурет].

[35 - сурет]

Салудың алгоритмі:

Қолөнерші (ремесленник) әдісімен салсақ

1.  Е нүктесінен шеңберді А нүктесінде қиятын ВС кесіндісіне перпендикульяр ЕВ кесіндісін сызамыз.

2.  Циркульді АВ кесіндісіне тең болатындай ашып бір басын ВС кесіндісіне қоямыз

3.  Бір басы ВС кесіндісінің бойымен жылжитындай циркульдің екі басын бірдей жылжытамыз.

Сонда АD кесіндісі дөңгелекке жүргізілген жанама болады.

Математикалық негіздеу: ЕВС=90, AD кесіндісі АВ парраллель болғандықтан ЕАD=90.  Шеңберге жүргізілген жанама радиусқа перпендикуляр болады

[IV] Егер ол: А нүктесінен ABC дөңгелегінің шеңберіне жанаманы қалай жүргізеді десе, онда А нүктесін дөңгелектің центрі D нүктесімен қосамыз, демек А мен D-ны [AD сызығымен] қосамыз. А нүктесінде AD сызығының бойымен DAE тікбұрышын тұрғызамыз. Сонда АЕ сызығы ABC дөңгелегіне жанама болады¹⁰. Міне оның суреті [36 - сурет].

[36 - сурет]

Салудың алгоритмі:

1.     А нүктесімен дөңгелектің D центрін қосамыз.

2.     А нүктесінен өтетін DAE тік бұрышын тұрғызамыз.

Сонда АD кесіндісі дөңгелекке жүргізілген жанама болады.

Математикалық негіздеу: Шеңберге жүргізілген жанама радиусқа перпендикуляр болады

[V] Егер ол АВС үшбұрышының АВ және АС сызықтарының арасына ВС-ға параллель болатын және егер ВС сызығы D сызығынан кіші болған жағдайда берілген D сызығына тең сызық сал десе, онда ВС сызығын оның бағытында [ВЕ D-ға тең болатындай Е нүктесіне дейін] созып, ал [егер ВС D сызығынан үлкен болса] D-ға тең ВЕ сызығын ВС сызығына саламыз. Е нүктесінен АВ сызығына параллель сызық жүргіземіз. Ол АС-ны G нүктесінде қиып өтеді. G нүктесінен ВС сызығына параллель сызық жүргіземіз; Бұл АВ-мен қиылысатын GH сызығы. Сонда GH D сызығана тең және ВС¹¹ сызығына параллель.  Міне оның суреті [37 - сурет].

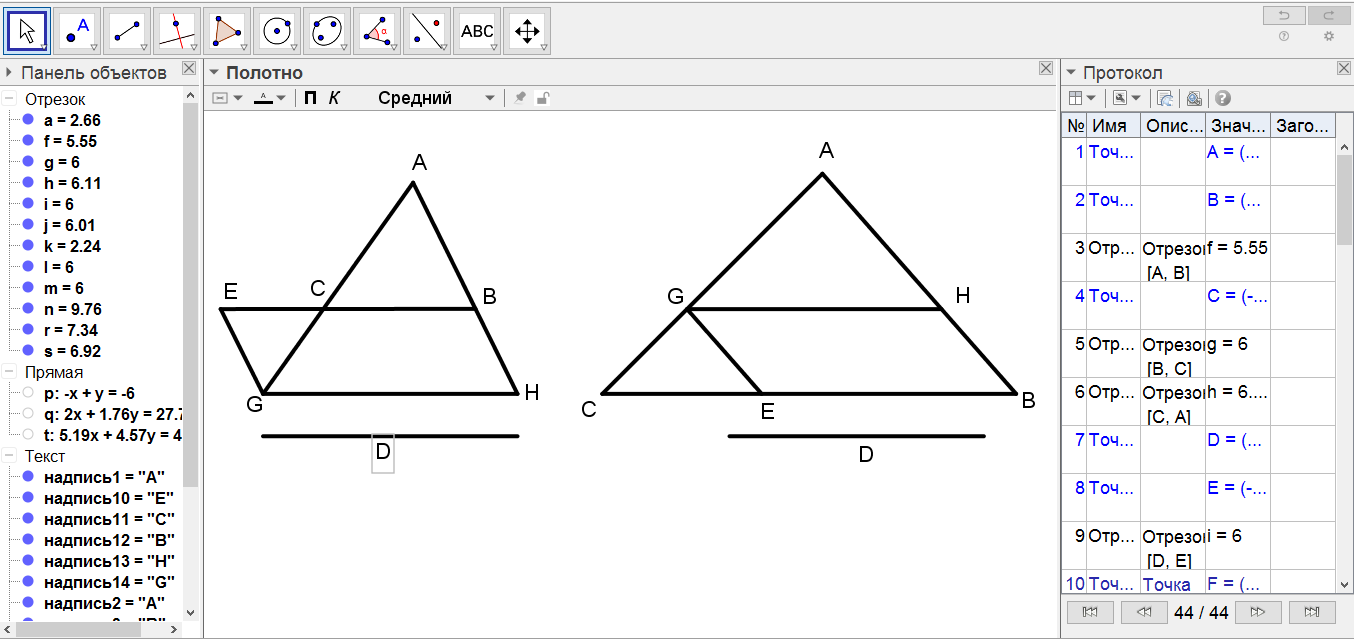
[37 - сурет]

Салудың алгоритмі:

1.     Егер ВС<D болса онда, ВС қабырғасын ВЕ=D болатындай Е нүктесіне дейін созамыз.

2.     Егер ВС>D болса онда, ВС қабырғасын ВЕ=D болатындай Е нүктесін белгілейміз.

3.     Е нүктесінен АВ қабырғасына параллель болатын ЕH кесіндісін саламыз.

4.     G нүктесінен CВ қабырғасына параллель болатын GH кесіндісін саламыз.

5.     Сонда GH=D болады.

Сонда HG BC қабырғасына параллель және HG=D кесіндісіне тең болады.

Математикалық негіздеу: Салу алгоритмінің өзі дәлелдеп тұр.

[VI] Егер ол АВС үшбұрышының АВ және АС сызықтарының арасына ВС сызығына параллель, мысалы АВ сызығында ол қиып алатын кесіндіге тең, яғни ЕВ сызығына тең DE сызығын салу керек болса, онда АСВ бұрышын BD сызығымен қақ бөлеміз де, D нүктесінен ВС-ға параллель DE сызығын жүргіземіз. Сонда DE сызығы ЕВ¹² сызығына тең. Міне оның суреті [38 - сурет].

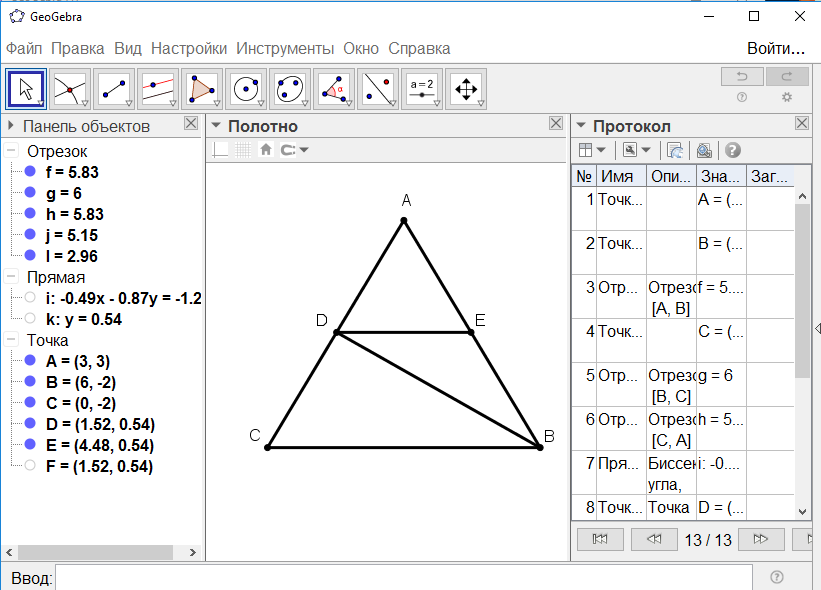
[38 - сурет]

Салудың алгоритмі:

1.     АВС бұрышын тең екіге бөлетіндей DE түзуін жүргіземіз.

2.     АС қабырғасында жататын D нүктесі арқылы ВС-ға параллель DЕ кесіндісін жүргіземіз.

3.     Сонда DE=EB болады.

Сонда DЕ ВС қабырғасына параллель және ЕВ және F кесіндісіне тең болады.

Математикалық негіздеу: CBD= ABD және СВ DE болғандықтын, CBD= BDE, демек BDЕ= DВЕ, яғни BDE үшбұрышы тең бүйірлі болғандықтын DE=EB болады.

 [VII] Егер ол АВС үшбұрышында, мысалы, ВС сызығына параллель және ВЕ мен F сызықтарына тең DE сызығын сал десе, онда ВС сызығына  F сызығына тең BG сызығын салып, G нүктесі арқылы АВ-ға параллель GH сызығын жүргізіп, HGC бұрышын қақ бөлетін GD сызығын [G нүктесі арқылы] жүргіземіз де D нүктесінен ВС сызығына параллель DE сызығын жүргіземіз. Сонда DE сызығы  ВЕ және F¹³ сызықтарына тең. Міне оның суреті [39 - сурет].

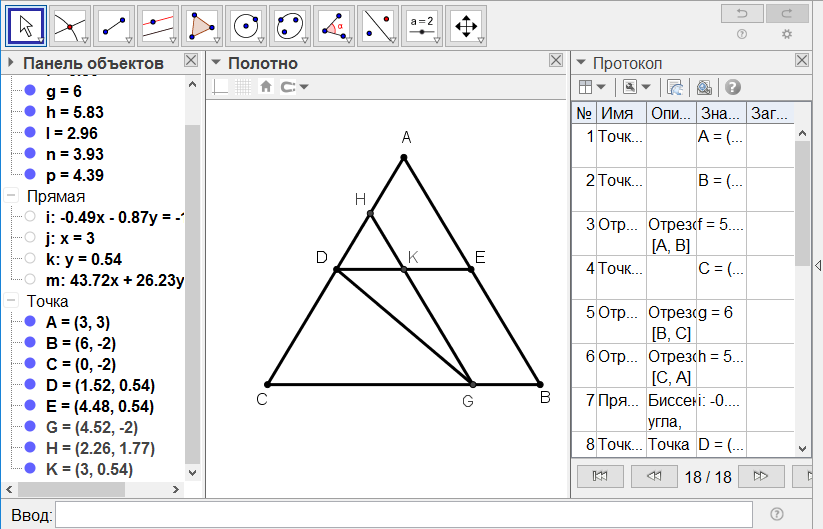
[39 - сурет]

Салудың алгоритмі:

1.     ВС қабырғасынын F кесіндісіне тең болатындай ВG кесіндісін белгілейміз.

2.     G нүктесінен АВ қабырғасына параллель болатын GH кесіндісін саламыз.

3.     HGC бұрышын қақ бөлетіндей GD кесіндісінін саламыз.

4.     D нүктесінен ВС қабырғасына параллель болатындай DЕ кесіндісін сызамыз.

Сонда DЕ ВС қабырғасына параллель және ЕВ және F кесіндісіне тең болады.

Математикалық негіздеу: Бұл есепте әл-Фараби жазбаларын аударғанда қате кетуі мүмкін. Салу алгоритмінің 4- қадамында DE сызығының орнына KE болған жағдайда  салу дұрыс болады.

[VIII] Басқа үшбұрышқа тең үшбұрышты салу туралы.  Егер ол қабырғалары басқа үшбұрыштың қабырғалырына тең үшбұрышты сал десе [мысалы АВС], онда DE түзу сызығын жүргіземіз де, АВ сызығына тең DG,  BC сызығына тең GH және СА тең HF сызығын  саламыз. G нүктесін центр ретінде қабылдап GD қашықтығында дөңгелек бөлігін келтірейік, сол сияқты H нүктесін центр ретінде қабылдап HF қашықтығында дөңгелек бөлігін келтіреміз. Бірінші бөлігі [екінші бөлігін] I нүктесінде қиып өтеді. Ары қарай GI және ІH сызықтарын жүргізейік. Онда GIH үшбұрышының қабырғалары АВС¹⁴ үшбұрышының қабырғаларына тең. Міне оның суреті [40 - сурет].

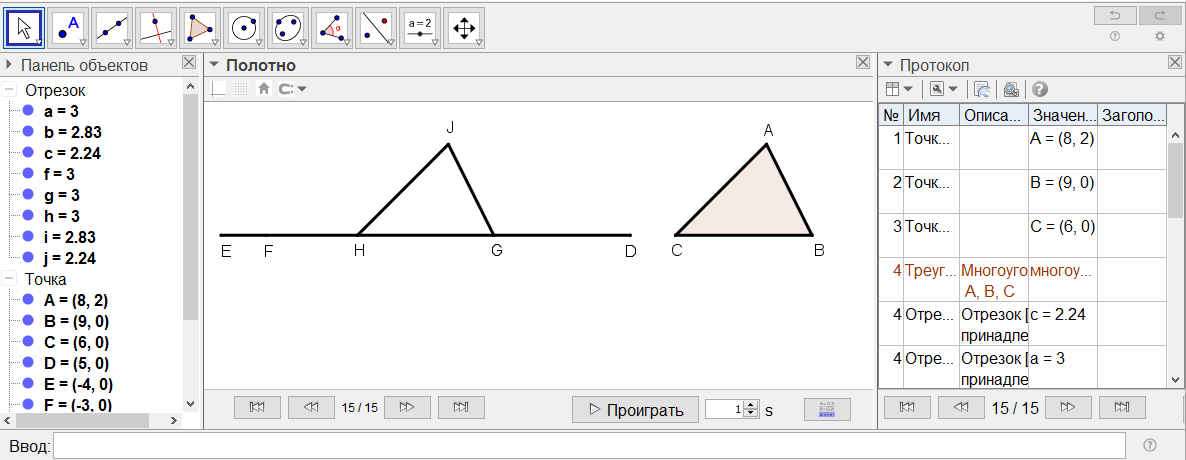
 [40 - сурет]

Салудың алгоритмі:

1.  DE түзуін сызып, оның бойынан DG=АВ, GH=BC, HF=CA болатындай DG,GH,HF кесінділерін белгілейміз.

2.  Центрі G болатындай r=GD жартышеңберін саламыз.

3.  Центрі H болатындайr=HF жартышеңберін саламыз. Екі жартышеңбер I нүктесінде қилысады.

4.  GI және IHтүзулерін жүргіземіз.

Сонда GIH үшбұрышы ABC үшбұрышына тең болады.

Математикалық негіздеу: Үшбұрыштар теңдігінің бірінші белгісі.

[IХ] Бұрышты тең үш бөлікке бөлу туралы. Егер ол АВС бұрышын тең үш бөлікке бөл десе, онда АВС бұрышы тік бұрышты болса, ВС сызығында тең қабырғалы DBC үшбұрышын тұрғызамыз. Сонда ABD бұрышы тік бұрыштың үштен бір бөлігі. DBC бұрышын қақ бөлеміз¹⁵.  Міне оның суреті [41 - сурет].

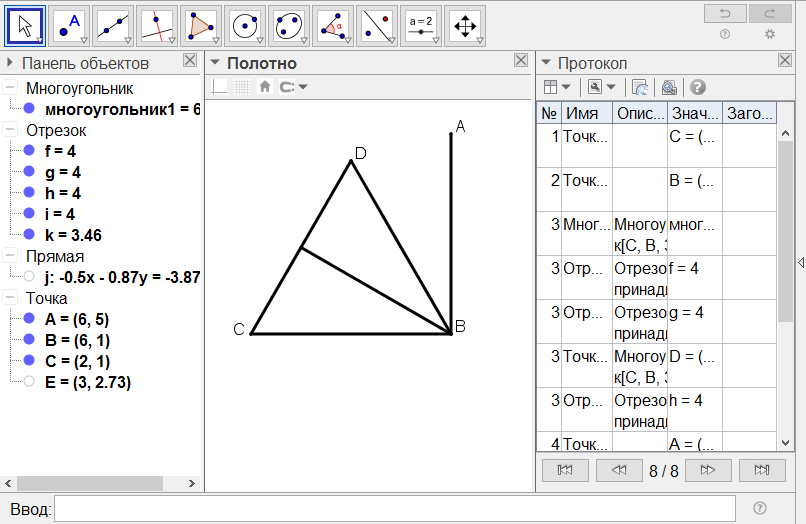
[41 - сурет]

Салудың алгоритмі:

1.  DС түзуіне тең қабырғалы DBC үшбұрышын тұрғызамыз.Сонда ABD бұрышы ABC бұрышының үштен біріне тең болады.

2.  DBC бұрышын қақ бөлеміз.

Сонда ABC бұрышы тең үшке бөлінеді.

Математикалық негіздеу: 90-60=30, 60:2=30

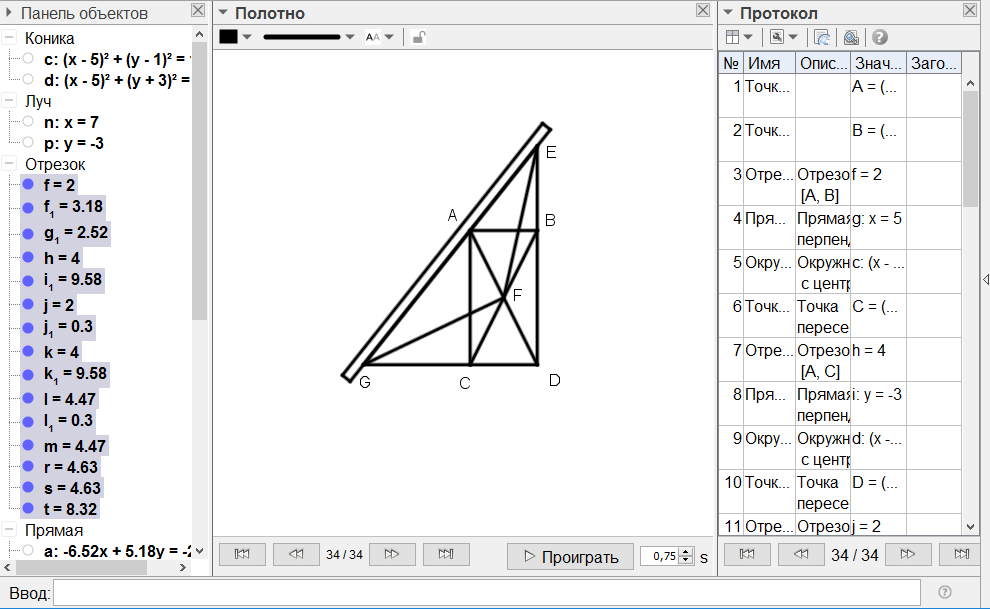
 [Х] Егер бұрыш тік бұрыштан кіші болса, онда В нүктесін центр ретінде қабылдап, ВА қашықтықта DAС дөңгелегін келтіреміз. BD ны ВС-ға тік бұрыш бойынша қойып, СВ-ны дөңгелекпен қиылысқанша Е нүктесіне созамыз. Сызғышты А нүктесіне әкеліп, оны CDE дөңгелегінің шеңбері бойынша DB перпендикуляры және DE доғасының арасында жатқан HF сызығы DB сызығына тең болғанша қозғайтын боламыз, бұл жағдайда сызғыш А нүктесінен таймайды. Ары қарай EF доғасына тең EK доғасын саламыз да, KB жүргізіп L нүктесіне дейінгі бағытта жалғаймыз. Онда LBC бұрышы АВС бұрышының үштен бірі болады. Әрі қарай ABL бұрышын қақ бөлеміз¹⁶. Міне оның суреті [42 - сурет].

[42 - сурет]

Салудың алгоритмі:

1.  В нүктесін центр етіп алып ВА қашықтықпен DAC шеңберін сызамыз.

2.  Сызғышты А нүктесіне қойып, BC ВD жүргіземіз.

3.  ВС түзуін шеңбермен Е нүктесінде қилысқанға дейін созамыз.

4.       Сызғыштың бір басын А нүктесіне қойып, екінші басын CDE шеңбері бойымен DB және DE перпендикульярларының арасында жататын HF =DB болғанға дейін жылжытамыз.

5.       EF доғасына тең EK доғасын тұрғызамыз.

6.       KB түзуін L нүктесіне дейін созамыз.

Сонда LBC бұрышы ABC бұрышының үштен біріне тең болады.

Математикалық негіздеу:

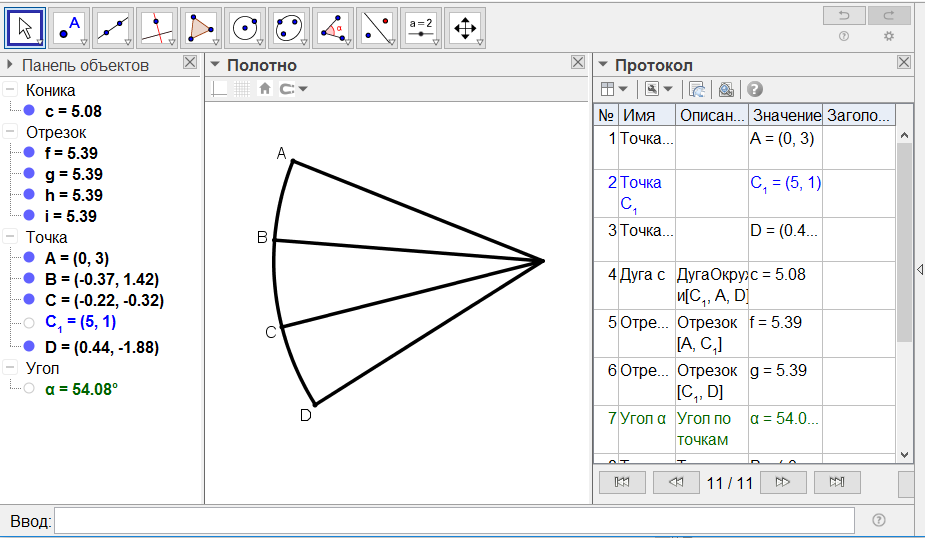
[ХІ] Бұрышты тең үшке бөлудің басқа тәсілі.  АВС сүйір бұрышын тұрғызайық та және егер біз оны тең үш бөлікке бөлгіміз келсе, А нүктесінен ВС сызығына AD параллелін және  А нүктесінен ВС сызығына AH перпендикулярын түсіреміз. В нүктесіне сызғышты әкеліп, AD мен AH сызықтарының арасына орналасқан сызық екі еселенген АВ болғанша қозғайтын боламыз. Бұл мысалы DEB сызығы, демек DE сызығы екі еселенген АВ сызығы болып табылады. Ендеше DBC бұрышы АВС¹⁷ бұрышының үштен бір бөлігі. Міне оның суреті [43 - сурет].

[43 - сурет]

Салудың алгоритмі: АВС сүйір бұрышын теңдей үшке бөлу керек болса, онда

1.  А нүктесінен AH ВC болатындай АН жүргіземіз.

2.  ВС параллель болатындай AD түзуін жүргіземіз.

3.  Сызғыштың бір басын В нүктесіне қойып, екінші басын ВD=2*AB болатындай BD түзуін жүргіземіз.

Сонда DBC бұрышы ABC бұрышының үштен біріне тең болады.

Математикалық негіздеу:

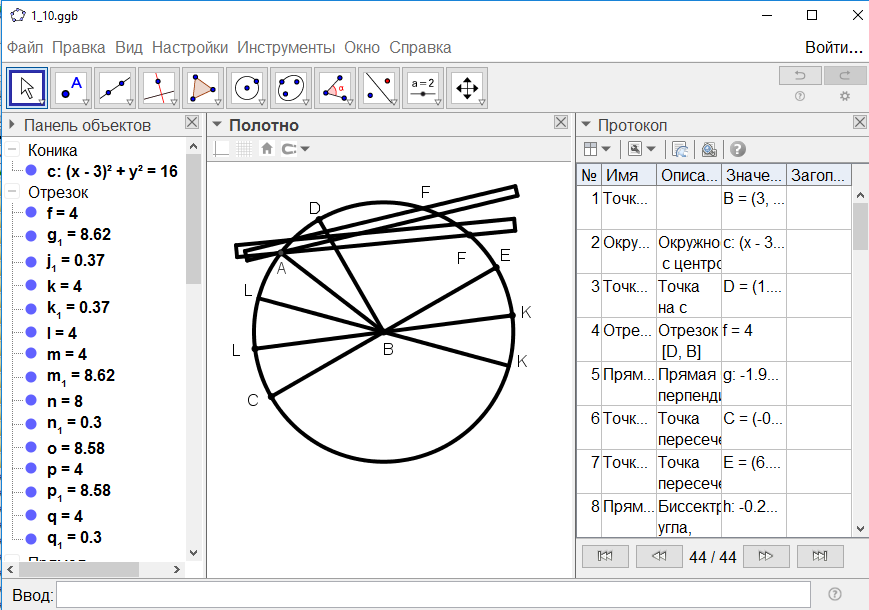
[ХІІ] Доғаны тең үш бөлікке бөлу туралы. Егер ол ABD доғасын тең үш бөлікке бөлу керек десе, онда осы доға орналасқан дөңгелектің центрін табамыз. Бұл Е нүктесі болсын. А мен Е-ні, Е мен D-ны қосып, ABCD доғасын В мен С нүктелерінде қиып өтетін ЕВ және ЕС сызықтарымен AED бұрышын үш тең бөлікке бөлеміз. Сонда ABCD доғасы үш тең бөлікке АВ, ВС және СD¹⁸ доғаларына бөлінетін болады. Міне оның суреті [44 - сурет].

[44 - сурет]

Салудың алгоритмі: АВС доғасын теңдей үшке бөлу керек болса, онда

1.  Доға орналасқан шеңбердің центрін тауып оны Е деп белгілейміз.

2.  AE және ED нүктелерін қосамыз.

3.  AED бұрышын теңдей үшке бөлеміз де, доғамен қилысу нүктелерін В және  С деп белгілейміз.

Сонда ABC[D] доғасы AB, BC және CD болып тең үшке бөлінеді.

Математикалық негіздеу: AED бұрышын теңдей үшке бөлгендіктен доға да тең үшке бөлінеді.

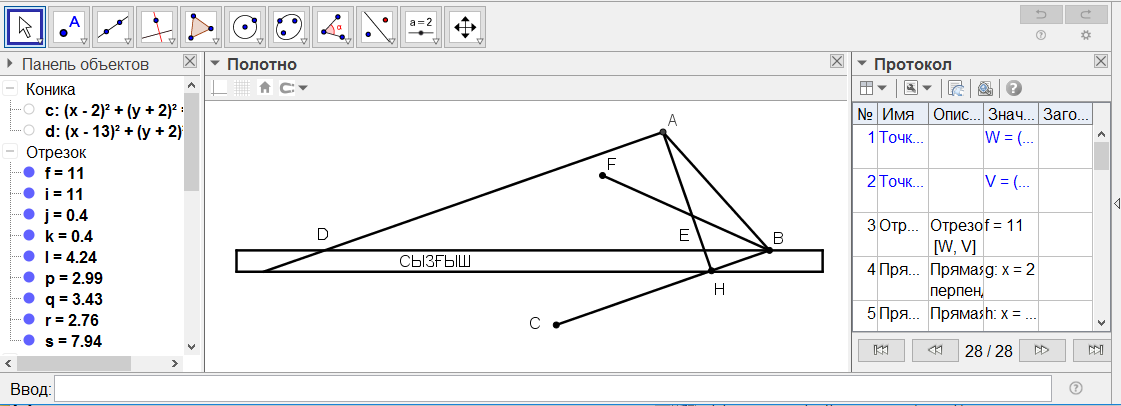
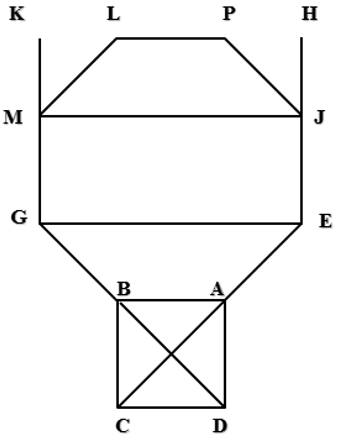
[ХІІІ] Екі еселенген басқа үйге немесе шарға тең немесе басқа қатынаста алынған үй немесе шар салу туралы. Егер ол ұзындығы, ені, биіктігі өзара тең екі еселенген басқа үй болып табылатын квадрат үйді салу керек болса немесе басқа екі еселенген болып келген шарды салу, немесе қақ бөліп немесе басқа бір қатынастарда болып табылатын шарды қалай салу керек десе, онда үй ұзындығына және шар диаметріне тең АВ сызығын тұрғызамыз, екі еселенген  тік бұрыш бойынша АВ сызығына АС сызығын салып, DABC жазық фигурасын толықтырамыз. AD мен ВС диагоналдарын жүргіземіз. Олар F нүктесінде қақ бөлінеді. Олардың бағытында DC мен DB сызықтарын созамыз. Cызғыштың шетін А нүктесіне қоямыз да оны GC және EB  сызықтары бойынша [ол оларды Е және G нүктелерінде қиылысқанша] GF пен FE тең болатындай болғанша қозғайтын боламыз.  Сонда үйдің ұзындығы немесе шардың диаметрі ВЕ¹⁹ сызығы болады.  Міне оның суреті [45 - сурет].

[45 - сурет]

Салудың алгоритмі: Берілген үйден екі есе, болмаса бірнеше есе үлкен биіктігі, ені және ұзындығы бірдей шаршы түрде үй немесе берілген шардан еселенген шарды немесе қақ бөлінген, болмаса басқа өлшемдегі шар салу керек болса, онда

1.  Шардың диаметріне немесе үйдің ұзындығына тең АВ кесіндісін саламыз.

2.  AВ-дан екі есе ұзын болатындай АС кесіндісін АВ-ға тік бұрышпен салып, пайда болған  фигураны DABC фигурасына толықтырамыз.

3.  AD және ВС диагональдарын жүргіземіз, олар F нүктесінде қилысады.

4.  DC және DB сызықтарын өз бағыттарымен созамыз.

5.  Сызғыштың қырын А төбесіне қоямыз да, GC және EB сызықтарының бойымен GF=FE (E және G нүктелерінде қияды деп есептейміз) болғанға дейін жылжытамыз.

Сонда үйдің ұзындығы немесе шардың диаметрі ЕВ болып табылады.

Математикалық негіздеу: Берілген бастапқы үйдің қабырғасын, немесе шардың радиусын a деп белгілесек, онда ол үйдің ауданы S=a², ал шардың ауданы S=pi*r² болатын еді, ал екі еселенген үйдің ауданы S_ү=2a² немесе екі еселенген шардың ауданы S=2pi*r² болуы керек. Яғни ЕВ=AB√2 болуы керек.

[ХІV] Өртегіш айна жасау туралы. Егер біз күн сәулелерінің көмегімен бір қашықтықтан затты өртейтін айнаны жасағымыз келсе, онда алдымен айнаны айқындайтын (лекало) даяр үлгісін жасайық. Ол үшін  дөңгелек салайық, оның жарты диаметрі өртегіміз келетін заттың арақашықтығының шамасына тең. Бұл АВС дөңгелегі болсын. Оның ADC диаметрін жүргізейік. DC сызығына С  нүктесінен бірнеше тең кесінділер салайық. Бұл кесінділер кіші болған сайын даяр үлгі жақсырақ және дәл болады. Бұл кесінділер CF, FH, HG, GE және ED болсын. D нүктесі арқылы [CD-ға] тік бұрыш бойынша E, G, H және F сызықтарын жүргізейік те, оларды екі жағына да B, I, K, L және М нүктелеріне дейін созайық. C мен В, С мен I, С мен K, С мен L, С мен М нүктелерін қосайық. CM сызығына тең FN сызығын, CL-ге тең HX, CK-ға тең GO, CI-ге тең EP және СВ-ға тең DS сызығын салайық. C, N, X, O, P және S нүктелерін қосайық та, осы сызық бойынша даяр үлгісін (лекало) жасайық. Сосын металдан, мысалы темірден, қоладан, мыстан немесе цинктен айна дайындайық та,  егер мүмкін болса, оны ысып жалтыратайық. Егер айна қисық болып шықса, оны даяр үлгісі бойынша даяр үлгіні айнаға С нүктесі даяр үлгінің ортасына дәл келетіндей айнаның даяр үлгімен беттесуіне қол жеткізетіндей етіп даяр үлгіні айнаға беттестіріп түзетеміз. Сонда үлкен өртегіш күші²⁰ бар өртегіш айнаны аламыз. Міне оның суреті [46 - сурет].

[46 - сурет]

Салудың алгоритмі: Егер күн сәулесі арқылы алыстағы затты жандыратын айна салу керек болса, онда алдымен айнаның қалыбын (лекало) жасап алу керек. Ол үшін

1.       Жарты диаметрі біз жағатын заттың қашықтығына тең болатындай шеңбер тұрғызамыз. Бұл шеңберді АВС деп алайық.

2.       AСD диаметрін жүргіземіз.

3.       DC түзуінің бойынан С нүктесінен бірдей бірнеше кесінділер сызамыз.

4.       Бұл кесінділер неғұрлым қысқа болған сайын қалыбымыз (лекало) соғұрлым дәл болады. Бұл кесінділерді CF, FH, HG, GE, ED деп алайық.

5.       D нүктесі арқылы өтетін, CD  түзуіне перпендикульяр E,G,H,F түзулерін екі бағытқа қарай B,I,K,L,M нүктелеріне дейін созамыз.

6.       C және B, C және I, C және K, C және L, C және M нүктелерін қосамыз.

7.       CM-ге тең FN, CL-ге тең HX, CK-ге тең GO, CI-ге тең EP, CB-ге тең DS түзулерін жүргіземіз.

8.       C,N,X,O,P және S нүктелерін қосып, осы сызықтар негізінде қалыпты жасаймыз.

9.       Содан соң айнаны металлдан жасаймыз. Мысалы темірден, болаттан, мыстан немесе цинктан жасаймыз, мүмкін болса барынша жалтыратамыз.

10.   Егер айна қисық болса, онда С нүктесін қалыптың ортасына келетіндей етіп айнаны түзетеміз. 

Сонда үлкен күші бар жандырғыш айна жасалады.

Математикалық негіздеу: CMF және   CNU үшбұрыштары ұқсас. CD=a, CF=x деп белгілесек  

[ХV] Өртегіш айна жасаудың екінші тәсілі.  Егер оны біз жасағымыз келсе, онда кез келген қашықтықты [оның жартысы АВ сызығы болсын] аламыз да, оны С нүктесіне дейінгі оның бағытына созамыз. В нүктесіне ВС-ға перпендикуляр DB сызығын қарама-қарсы екі жағына да орнатайық та, ВС сызығына өзара тең кіші сызықтарды BE, EG, GH және HC салайық. F нүктесінде АЕ-ні қақ бөліп, F центрінен FA  қашықтықта дөңгелек сызайық. Ол BD сызығын I нүктелерінде қияды. I нүктелерінен AC сызықтарына параллель IL сызықтарын жүргізейік те  Е нүктесінен BD сызығына параллель сызықты L нүктелеріне дейін жүргізейік. Сосын AG сызығын М нүктесінде қақ бөліп, М нүктесінен  МА қашықтықта дөңгелек сызамыз. Ол BD сызығын N нүктелерінде қияды. N нүктелерінен АС сызығына параллель NX сызықтарын Х нүктесіне дейін жүргіземіз. Сосын АН сызығын О нүктесінде қақ бөліп, О центрінен ОА қашықтықта дөңгелек сызамыз. Ол BD сызығын Р нүктелерінде қияды. Р нүктелерінен ВС-ға параллель Z нүктелеріне дейін сызықтар жүргізейік. B, L, X және Z нүктелерін сызықпен қосып, даяр үлгі аламыз. Егер біз даяр үлгіні тексеретін болсақ, оны В нүктесін айнаның ортасына орналастырамыз. Сонымен біз үлкен өртегіш күші бар өртегіш айна аламыз²¹.  Міне оның суреті [47 - сурет].

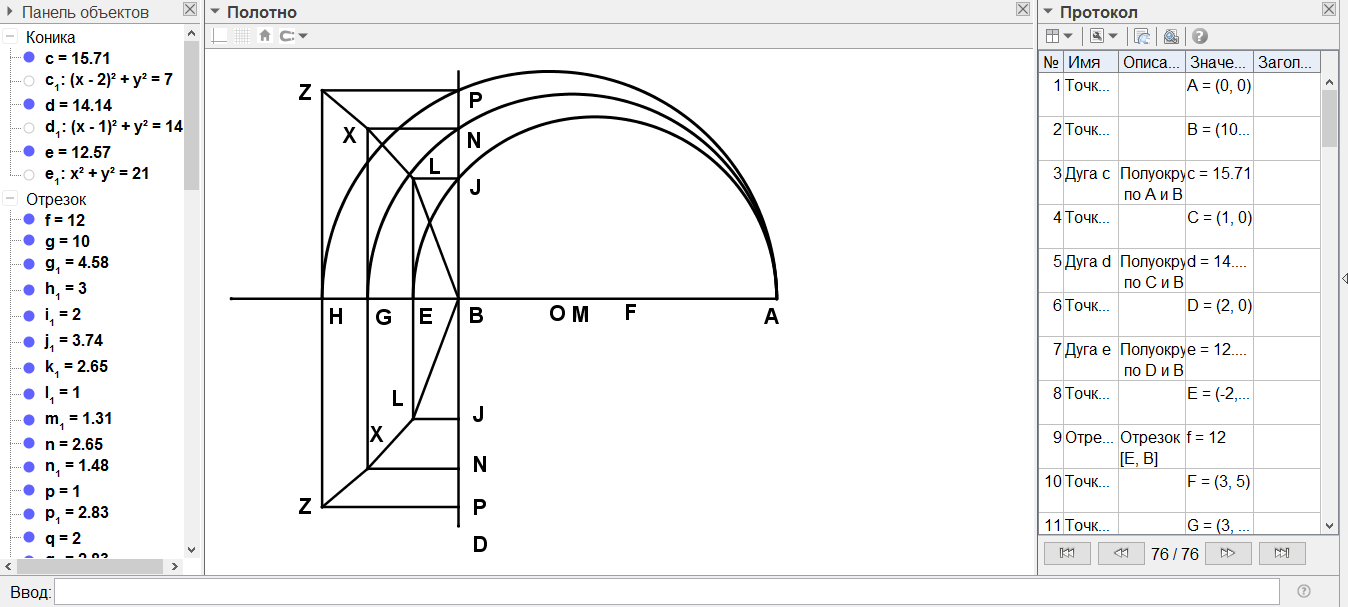
[47 - сурет]

Салудың алгоритмі: Егер күн сәулесі арқылы алыстағы затты жандыратын айна салу керек болса, онда

1.       Жартысы АВ –ға тең болатындай кез-келген қашықтықтағы Жарты диаметрі біз жағатын заттың қашықтығына тең болатындай шеңбер тұрғызамыз. Бұл шеңберді АВС деп алайық.

2.       AСD диаметрін жүргіземіз.

3.       DC түзуінің бойынан С нүктесінен бірдей бірнеше кесінділер сызамыз.

4.       Бұл кесінділер неғұрлым қысқа болған сайын қалыбымыз (лекало) соғұрлұм дәл болады. Бұл кесінділерді CF, FH, HG, GE, ED деп алайық.

5.       D нүктесі арқылы өтетін, CD  түзуіне перпендикульяр E,G,H,F түзулерін екі бағытқа қарай B,I,K,L,M нүктелеріне дейін созамыз.

6.       C және B, C және I, C және K, C және L, C және M нүктелерін қосамыз.

7.       -CM-ге тең FN, CL-ге тең HX, CK-ге тең GO, CI-ге тең EP, CB-ге тең DS түзулерін жүргіземіз.

8.       C,N,X,O,P және S нүктелерін қосып, осы сызықтар негізінде қалыпты жасаймыз.

9.       Содан соң айнаны металлдан жасаймыз. Мысалы темірден, болаттан, мыстан немесе цинктан жасаймыз, мүмкін болса барынша жалтыратамыз.

10.   Егер айна қисық болса, онда С нүктесін қалыптың ортасына келетіндей етіп айнаны түзетеміз. 

Сонда үлкен күші бар жандырғыш айна жасалады.

Математикалық негіздеу: Бұл есептің дәлелдеуі де алдыңғы есеппен ұқысас.

Салудың алгоритмі:

1.     A және В нүктелерін центр етіп алып, АВ қашықтықта шеңберлер жүргіземіз.

2.  Бұл шеңберлер С нүктесінде қилысады.

3.  С нүктесін А және В нүктелерімен СА және СВ түзу сызықтармен қосамыз.

Сонда АВС үшбұрышы тең қабырғалы болып табылады.

Математикалық негіздеу: Тікбұрышты үшбұрышқа сырттай сызылған шеңбердің ценрі гипотенузаның  қақ ортасында жатады.

[ІІ] Шаршы салу туралы. Егер ол АВ сызығына тең қабырғалы [және тең бұрышты] төртбұрышты қалай тұрғызамыз десе, онда А мен В нүктелерінің әрқайсысына перпендикуляр өзара тең АВ сызықтарын орнатамыз. Ол - АС мен ВD сызықтары. С мен D-ны қосып  тең қабырғалы [және тең бұрышты] ABCD²³ төртбұрышын аламыз. Міне оның суреті [49 - сурет].

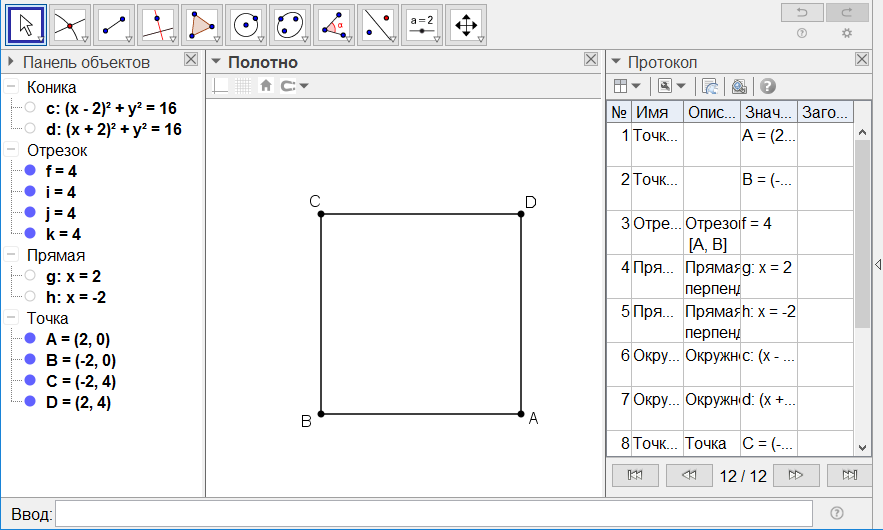
[49 - сурет]

Салудың алгоритмі:

1.  А және В төбелеріне АВ-ға тең болатындай АС және BD перпендикулярларын тұрғызамыз.

2.   С және D нүктелерін қосып, ABCD тең қабырғалы (және тең бұрышты) төртбұрышын саламыз.

Сонда АВСD төртбұрышы тең қабырғалы (және тең бұрышты)  болып табылады.

Математикалық негіздеу: Шеңберге жүргізілген жанама радиусқа перпендикуляр болады.

[ІІІ] Бесбұрышты салу туралы. Егер ол АВ сызығында тең қабырғалы бесбұрышты қалай тұрғызайық десе, онда В нүктесіне АВ-ға тең ВС перпендикулярын орнатамыз. АВ [сызығын] D нүктесінде қақ бөліп, D нүктесін центрі ретінде DC қашықтықта CE доғасын сызамыз да, АВ сызығын Е нүктесіне дейін созамыз. Сосын А мен В нүктелерінің әрқайсысын центрі ретінде алып АЕ қашықтықта доғалар сызамыз. Олар G нүктесінде қиылысады. AG және BG  сызықтарын жүргізейік. ABG үшбұрышын - бесбұрыштың үшбұрышын аламыз. Бұл көптеген салуларда қажет болады. Содан соң А мен G нүктелерін центрлер ретінде алып, АВ қашықтықта доғалар сызамыз. Олар Н нүктесінде қиылысады. Сосын центрлері ретінде В мен G нүктелерінен F нүктесінде қиылысатын доғалар сызамыз.  AH, HG, GF және FB сызықтарын жүргізіп, тең қабырғалы, тең бұрышты ABFGH²⁴ бесбұрышын аламыз. Міне оның суреті [50 - сурет].

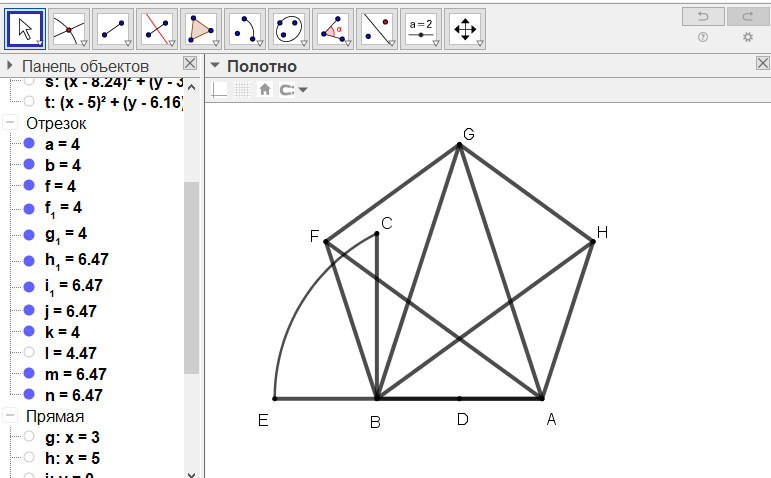
[50 - сурет]

Салудың алгоритмі:

Егер ол АВ сызығында тең қабырғалы бесбұрышты қалай тұрғызайық десе, онда

1.     В нүктесіне АВ-ға тең ВС перпендикулярын орнатамыз.

2.     АВ [сызығын] D нүктесінде қақ бөлеміз

3.     D нүктесін центрі ретінде алып, DC қашықтықта CE доғасын сызамыз

4.     АВ сызығын Е нүктесіне дейін созамыз.

5.     А мен В нүктелерінің әрқайсысын центрі ретінде алып АЕ қашықтықта доғалар сызамыз.

6.     Олар G нүктесінде қиылысады. AG және BG  сызықтарын жүргіземіз. Сонда ABG үшбұрышын - бесбұрыштың үшбұрышын аламыз. Бұл көптеген салуларда қажет болады.

7.     Содан соң А мен G нүктелерін центрлер ретінде алып, АВ қашықтықта доғалар сызамыз.

8.     Олар Н нүктесінде қиылысады. Сосын центрлері ретінде В мен G нүктелерінен F нүктесінде қиылысатын доғалар сызамыз.

9.     AH, HG, GF және FB сызықтарын жүргізіп, тең қабырғалы, тең бұрышты ABFGH²⁴ бесбұрышын аламыз.

Математикалық негіздеу:  Дұрыс бесбұрыштың диагональдарының ұзындығы 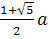   екендігі белгілі. Ал, берілген алгоритм бойынша AB қабырғасын 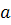-ға тең деп алсақ,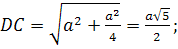 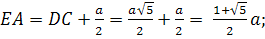     Яғни берілген алгоритм бойынша сызылған бесбұрыш дұрыс бесбұрыш болып табылады.

[IV] Егер ол АВ сызығына тең циркуль ашасымен ғана, оның күйі өзгермейтіндей етіп  АВ сызығына тең қабырғалы бесбұрыш тұрғыз десе, онда АВ сызығына оған перпендикуляр АВ сызығына тең ВС сызығын орнатамыз.  АВ сызығын D нүктесінде қақ бөліп, С-мен қосамыз да D нүктесін центр ретінде алып, АВ қашықтықта DC сызығында I нүктесін белгілейміз, DI-ді K нүктесінде қақ бөліп, АВ сызығын Е нүктесінде қиып өтетін K нүктесіне KE перпендикулярын тұрғызамыз. Ары қарай  А мен Е нүктелерінің әрқайсысынан центрлері ретінде АВ қашықтықта доғалар сызамыз. Олар М нүктесінде қиылысады. ВМ-ді жүргізіп, оны G-ға дейін оның бағытында созамыз да, MG-ді АВ сызығына тең етеміз. А мен G -ді қосамыз. А мен G-ді центрлер ретінде қабылдап, АВ қашықтықта Н нүктесін белгілейік. B мен G нүктелерін центрлер ретінде қабылдап, АВ қашықтықта А нүктесін белгілейік. AH, HG, GF және FB сызықтарын жүргізейік. Тең қабырғалы AFBGH²⁵ бесбұрышы шығады. Міне оның суреті [51-сурет].

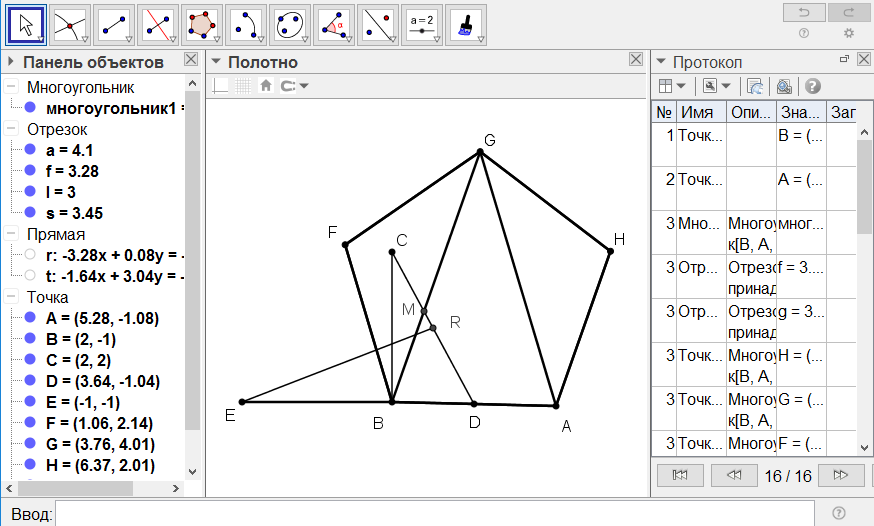
[51 - сурет]

Салудың алгоритмі:

1.     АВ сызығына оған перпендикуляр АВ сызығына тең ВС сызығын орнатамыз. 

2.     АВ сызығын D нүктесінде қақ бөліп, С-мен қосамыз да D нүктесін центр ретінде алып, АВ қашықтықта DC сызығында I нүктесін белгілейміз

3.     DI-ді K нүктесінде қақ бөліп, АВ сызығын Е нүктесінде қиып өтетін K нүктесіне KE перпендикулярын тұрғызамыз.

4.     А мен Е нүктелерінің әрқайсысынан центрлері ретінде АВ қашықтықта доғалар сызамыз. Олар М нүктесінде қиылысады.

5.     ВМ-ді жүргізіп, оны G-ға дейін оның бағытында созамыз да, MG-ді АВ сызығына тең етеміз.

6.     А мен G -ді қосамыз.

7.     А мен G-ді центрлер ретінде қабылдап, АВ қашықтықта Н нүктесін белгілейік.

8.      B мен G нүктелерін центрлер ретінде қабылдап, АВ қашықтықта А нүктесін белгілейік. AH, HG, GF және FB сызықтарын жүргіземіз.

Сонда тең қабырғалы AFBGH²⁵ бесбұрышы шығады

Математикалық негіздеу: Дұрыс бесбұрыштың диагональдарының ұзындығы 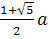  екендігі белгілі. Ал, берілген алгоритм бойынша AB қабырғасын 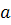-ға тең деп алсақ,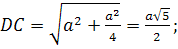 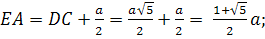    Яғни берілген алгоритм бойынша сызылған бесбұрыш дұрыс бесбұрыш болып табылады.

[V] Алты бұрышты салу туралы. Егер ол АВ сызығына тең қабырғалы және [тең бұрышты] алты бұрыш тұрғыз десе, онда ол үшін тең қабырғалы АВС үшбұрышын тұрғызамыз. АС мен ВС сызықтарын олардың бағыттарында Е мен G нүктелеріне дейін созайық. ВС-да тағы бір тең қабырғалы ВСD үшбұрышын тұрғызайық. DC сызығын оның бағытында Н нүктесіне дейін созып, СЕ, CG және СН сызықтарын СА сызығына тең етеміз де, DE, EG, GH және НА сызықтарын жүргіземіз. Тең қабырғалы және тең бұрышты ABDEGH²⁶ алты бұрышы шығады. Міне оның суреті [52 - сурет].

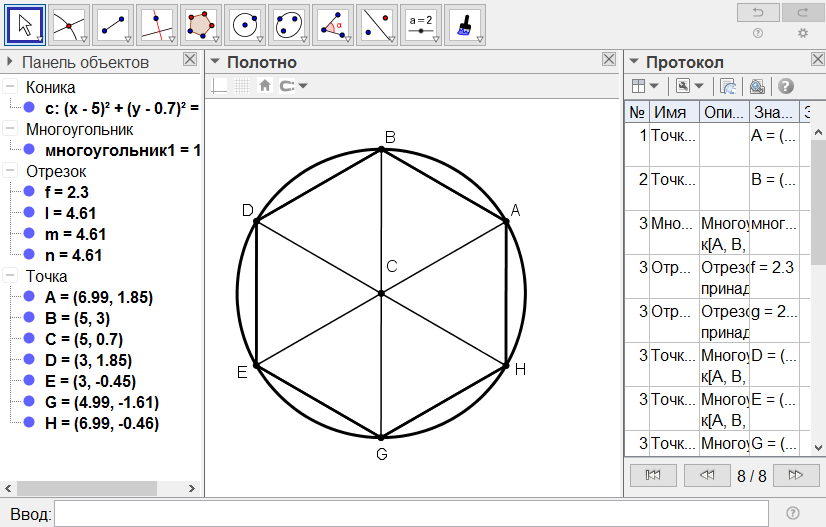
[52 - сурет]

Салудың алгоритмі:

1-қадам. AB  кесіндісі арқылы дұрыс ABC үшбұрышын саламыз.

2-қадам. C нүктесі арқылы AC мен BC кесінділерін бір бағытта AB кесіндісінің ұзындығына тең ұзындыққа созамыз.

3-қадам. Созылған кесінділердің ұштарын D және E деп белгілеп, оларды қосамыз.

4 -қадам. AC  кесіндісі арқылы дұрыс ACG үшбұрышын саламыз.

5-қадам. C нүктесі арқылы CG кесіндісін  AB кесіндісінің ұзындығына тең ұзындыққа созып, оның ұшын K деп аламыз.

6-қадам. G мен D-ны, E мен K-ны және K мен B-ны қосамыз.

Математикалық негіздеу: Дұрыс алтыбұрыштың ішкі бұрышы 120⁰ тең болады. Салынған алтыбұрыштың қабырғаларының теңдігі, AGC, GCD, DEC, ECK және KCB үшбұрыштарының өзара тең дұрыс үшбұрыш болатындығынан шығады. Ал, дұрыс үшбұрыштың ішкі бұрышы 60⁰-қа тең болғандықтан, салынған алтыбұрыштың әрбір ішкі бұрышы 120⁰-қа тең екендігі шығып тұр. Яғни берілген алгоритм бойынша сызылған алтыбұрыш дұрыс алтыбұрыш болып табылады.

[VI] Жеті бұрышты салу туралы. Егер ол АВ сызығына тең қабырғалы жеті бұрышты тұрғыз десе, онда ВС сызығын АВ сызығына тең етіп, АС сызығына тең қабырғалы DАС үшбұрышын тұрғызамыз да бесінші тарауда көрсетілгендей АВС үшбұрышына сырттай дөңгелек сызамыз. Онда АВ сызығына тең АЕ сызығын-хорданы жүргізіп G нүктесінде АЕ-ні қақ бөлеміз, GH перпендикулярын орнатып, оны дөңгелек шеңберіне дейін созамыз. АВ-ны F нүктесінде қақ бөліп, оған GH перпендикулярына тең FI перпендикулярын тұрғызайық. А, В және I нүктелері арқылы ABI дөңгелегін жүргізіп [оған] АВ доғасына тең АК, KL, LI, IM, MN және NB доғаларын саламыз. АК, KL, LI, IM, MN және NB сызықтарын жүргізейік; бұл тең қабырғалы және тең бұрышты жеті бұрыш²⁷. Міне оның суреті [53 - сурет].

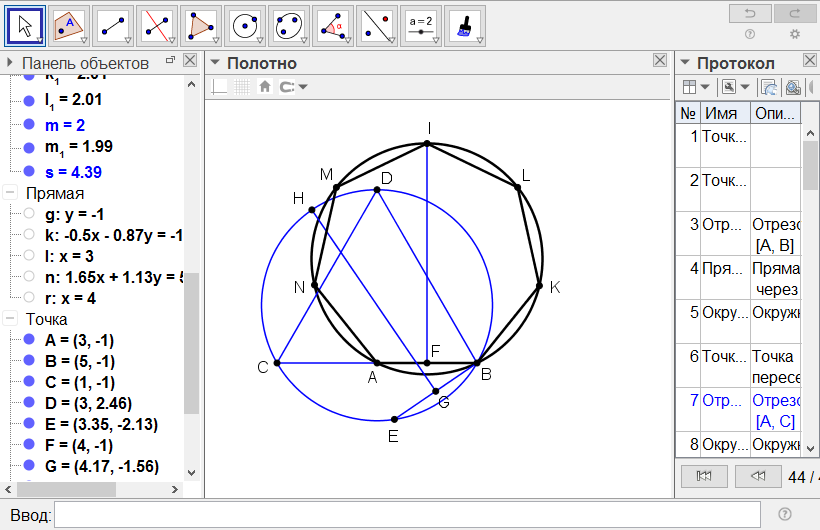
[53 - сурет]

Салудың алгоритмі:

1-қадам. АВ кесіндісін АВ =AC болатындай C нүктесіне созамыз.

2-қадам.   CB кесіндісі арқылы дұрыс (дұрыс үшбұрыш салу алгоритмін пайдаланып)  BCD үшбұрышын саламыз

3-қадам.   сырттай w1 шеңберін саламыз

4-қадам. B нүктесінен BE=AB болатындай  w1  шеңберіне BЕ хордасын саламыз және оның қақ ортасын G деп аламыз.

5-қадам. G нүктесінен BE хордасына перпендикуляр кесінді жүргізіп, оның w1 шеңберімен қыйылысу нуктесін H деп аламыз.

6-қадам.АВ кесіндісінің центрін F деп алып, ол нүктеден AB-ға ұзындығы GH кесіндісіне тең болатындай FI перпендикулярын саламыз.

7-қадам. А, В және I нүктелері арқылы w2 шеңберін сызамыз.

8-қадам.  w2 шеңберіне B нүктесінен бастап, ұзындығы AB кесіндісінің ұзындығына тең болатын, BK, KL, LI, IM, MN және NA хордаларын сызамыз.

Математикалық негіздеу: AB=BE, GH=FI, HG мен EB перпендикуляр, ал FI мен AB перпендикуляр және AF, FB, EG,GB кесінділері өзара тең болғандықтан w1 шеңбері мен w2 шеңберінің радиустері тең екендігі шығады. Алдымен w1 шеңберінің радиусын анықтап алайық. w1 шеңбері BCD дұрыс үшбұрышына сырттай сызылған шеңбер болғандықтан, оның радиусы дұрыс үшбұрышқа сырттай сызылған шеңбердің радиусының формуласына сәйкес төмендегідей болады;

                           R_w1=BC/                            (2.6)

AB кесіндісін бірлік кесінді деп алатын болсақ, BC=2AB=2, сонда шығатыны:

                            R_w1=2/                               (2.7)

 Келесі кезекте қабырғасы бірлік кесінді деп алынған дұрыс жетібұрыш бар деп алып, оған сырттай сызылған шеңбердің радиусын анықтайық. Қабырғасы a болатын дұрыс n бұрышқа сырттай сызылған шеңбердің радиусының формуласы төмендегідей болады:

                        R=                                  (2.8)  

Сонда, қабырғасы бірлік кесінді болатын, дұрыс жетібұрышқа сырттай сызылған шеңбердің радиусының мәні:

                         R=                                   (2.9)

   Берілген алгоритм бойынша сызылған жетібұрыш дұрыс жетібұрыш болып табылады, егер (7.2) теңдігі анықталған радиус пен (7.4) теңдігі анықталған радиустың мәндері бірдей болса. Ал бұл аталған мәндер sin( /4  шамасына тең болса ғана өзара тең болып табылады. Енді бұл аталған мәндердің әртүрлі дәлдікпен алынған сан мәндерін салыстыру кестесін келтірейік.

sin(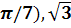 /4  шамаларының әртүрлі дәлдіктегі мәндері

[VIІ] Сегіз бұрышты салу туралы. Егер ол АВ сызығына тең қабырғалы сегіз бұрышты қалай тұрғызу керек десе, онда АВ-ны оның бағытында С мен D нүктелеріне дейін созып А мен В нүктелерінің әрқайсысы үшін тікбұрыштың жартысына тең ЕАС және GBD бұрыштарын саламыз. АЕ және BG сызықтарының әрқайсысын АВ сызығына тең етіп алып Е мен G нүктелерінің әрқайсысынан DC сызығына ЕС және GD перпендикулярын түсіреміз де CHKD шаршысын толықтырамыз. HI, HF, KL және KM сызықтарының әрқайсысын СЕ сызығына тең етіп алып I және F,  L және M-ді қосамыз. Тең қабырғалы ABGMLFIE²⁸ сегіз бұрышы шығады. Міне оның суреті [54 - сурет].

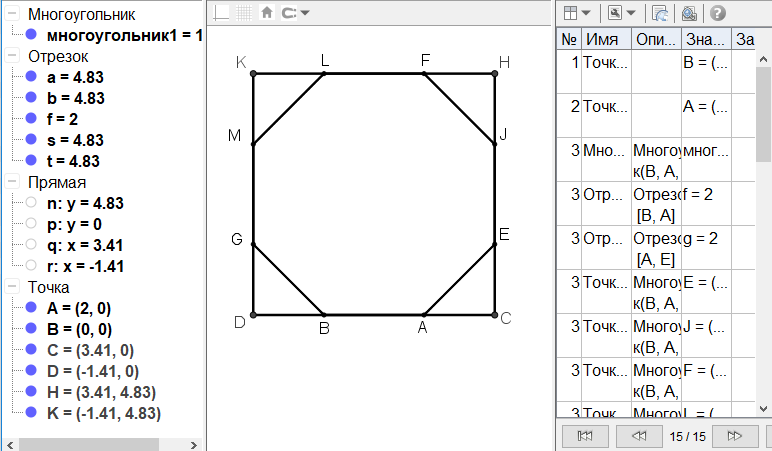
[54 сурет].

Салудың алгоритмі:

Егер ол АВ сызығына тең қабырғалы сегіз бұрышты қалай тұрғызу керек десе, онда

1.     АВ-ны оның бағытында С мен D нүктелеріне дейін созамыз.

2.     А мен В нүктелерінің әрқайсысы үшін тікбұрыштың жартысына тең ЕАС және GBD бұрыштарын саламыз.

3.     АЕ және BG сызықтарының әрқайсысын АВ сызығына тең етіп аламыз.

4.     Е мен G нүктелерінің әрқайсысынан DC сызығына ЕС және GD перпендикулярын түсіреміз.

5.     CHKD шаршысын толықтырамыз.

6.     HI, HF, KL және KM сызықтарының әрқайсысын СЕ сызығына тең етіп аламыз.

7.     I және F,  L және M-ді қосамыз. Сонда тең қабырғалы ABGMLFIE²⁸ сегіз бұрышы шығады.

Математикалық негіздеме:

<DBC=45⁰, <EAC=45⁰;

AB=EA, CD=AB;

<DCH=90⁰, <KDC=90⁰;

HI=CE, HF=CE, KL=CE және KM= СЕ болғандықтан MG=GB=BA=AE=EJ=JF=FL=LM, ал  <EAB=<ABG=<BGM=<GML=<MLF=<LFJ=<FGE=<JEA=135⁰, яғни бұл дұрыс сегізбұрыш болып табылады.

[VIІІ] Егер ол АВ сызығына тең циркуль ашасымен ғана, оның күйі өзгермейтіндей етіп,  АВ сызығына тең қабырғалы сегіз бұрыш тұрғыз десе, онда АВ сызығына тең қабырғалы және тең бұрышты ABCD төртбұрышын тұрғызып, СА және BD сызықтарын жүргіземіз де, олардың бағыттарында Е және G нүктелеріне дейін созамыз. АЕ мен BG сызықтарының әрқайсысын АВ сызығына тең етіп алып EG-ны қосамыз, EG сызығына АВ сызығына тең [EI және GM] перпендикулярларын орнатамыз да M және I-ді қосамыз. ЕІ мен GM сызықтарының әрқайсысын олардың бағыттарында К және Н нүктелеріне дейін созамыз да, IMK және MIH бұрыштарының әрқайсысын MLF сызықтарымен қақ бөлеміз. ML және ІF сызықтарының әрқайсысын АВ сызығына тең етіп алып FL-ді қосайық.  Тең қабырғалы тең бұрышты ABGMLFIE²⁹ сегіз бұрышы шығады. Міне оның суреті [55 - сурет].

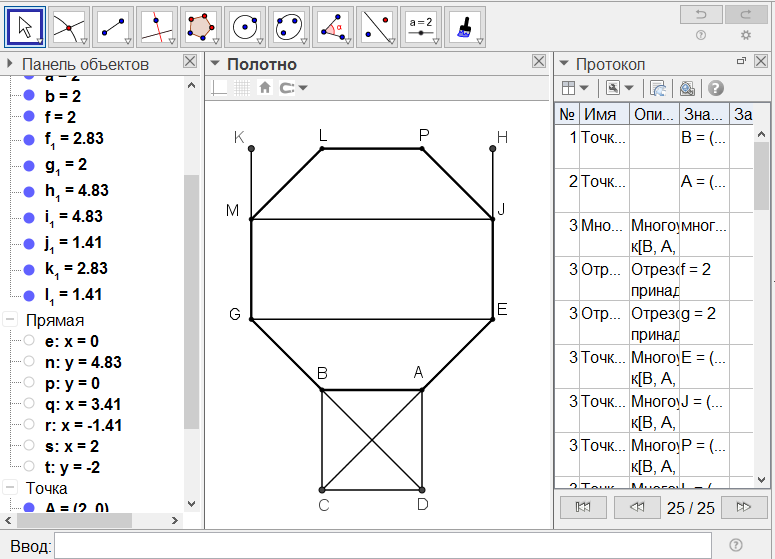
[55 сурет].

Салудың алгоритмі: Егер ол АВ сызығына тең циркуль ашасымен ғана, оның күйі өзгермейтіндей етіп,  АВ сызығына тең қабырғалы сегіз бұрыш тұрғыз десе, онда

1.     АВ сызығына тең қабырғалы және тең бұрышты ABCD төртбұрышын тұрғызамыз

2.     СА және BD сызықтарын жүргіземіз де, олардың бағыттарында Е және G нүктелеріне дейін созамыз.

3.     АЕ мен BG сызықтарының әрқайсысын АВ сызығына тең етіп алып EG-ны қосамыз

4.     EG сызығына АВ сызығына тең [EI және GM] перпендикулярларын орнатамыз

5.     M және I-ді қосамыз.

6.     ЕІ мен GM сызықтарының әрқайсысын олардың бағыттарында К және Н нүктелеріне дейін созамыз

7.     IMK және MIH бұрыштарының әрқайсысын MLF сызықтарымен қақ бөлеміз.

8.     ML және ІF сызықтарының әрқайсысын АВ сызығына тең етіп алып FL-ді қосамыз. Сонда тең қабырғалы тең бұрышты ABGMLFIE²⁹ сегіз бұрышы шығады.

Математикалық негіздеме: Салынған сегізбұрыштың қабырғаларының ұзындықтарының теңдігі, берілген алгоритмнің қадамдарынан айқын көрініп тұр. Енді бұл сегізбұрыштың ішкі бұрыштарының әр қайсысы 135⁰-қа тең екендігін дәлелдеуіміз керек.

ABCD дұрыс төртбұрыш болғандықтан:

<BAC=45⁰, <ABD=45⁰

Бұдан шығатыны:

<EAB=180⁰-45⁰=135⁰,  <GBA=180⁰-45⁰=135⁰

AB мен EG кесінділері параллел болғандықтан:

<AEG=<BAC=45⁰, <BGE=<ABD=45⁰

Бұдан шығатыны:

<IEA=90⁰+45⁰=135⁰,  <MGB=90⁰+45⁰=135⁰

FIM және HMI бұрыштары тік бұрышты қақ бөлетіндіктен:

<FIE=90⁰+45⁰=135⁰,  <LMG=90⁰+45⁰=135⁰

Яғни берілген алгоритм бойынша сызылған сегізбұрыш дұрыс сегізбұрыш болып табылады.

[IX] Тоғызбұрышты салу туралы. Егер ол АВ сызығына тең қабырғалы және тең бұрышты тоғыз бұрыш тұрғызу керек десе, онда центрі G нүктесі болатын кез келген өлшемді  CDE дөңгелегін сызып, ондағы С нүктесін белгілеп оны центр ретінде қабылдайық та дөңгелектен жарты диаметрлік қашықтықта Е мен D нүктелерін белгілейік. DE доғасын тең үш бөлікке бөлейік. Сондай доғаның бірі EH болсын. EG, EH және HG сызықтарын жүргізіп, EG мен HG сызықтарының арасында АВ сызығына тең және ЕН сызығына параллель FI сызығын саламыз. А мен В нүктелерін центр ретінде қабылдап FG қашықтықта К нүктесінде қиылысатын дөңгелектер сызайық. К нүктесін центр ретінде қабылдап KА қашықтықта ABL дөңгелегін сызамыз. ABL доғасын тең сегіз бөлікке бөліп, олардың бөліну нүктелерін хордалармен қосайық. АВ³⁰ сызығында тең қабырғалы және тең бұрышты тоғыз бұрыш шығады. Міне оның суреті [56 - сурет].

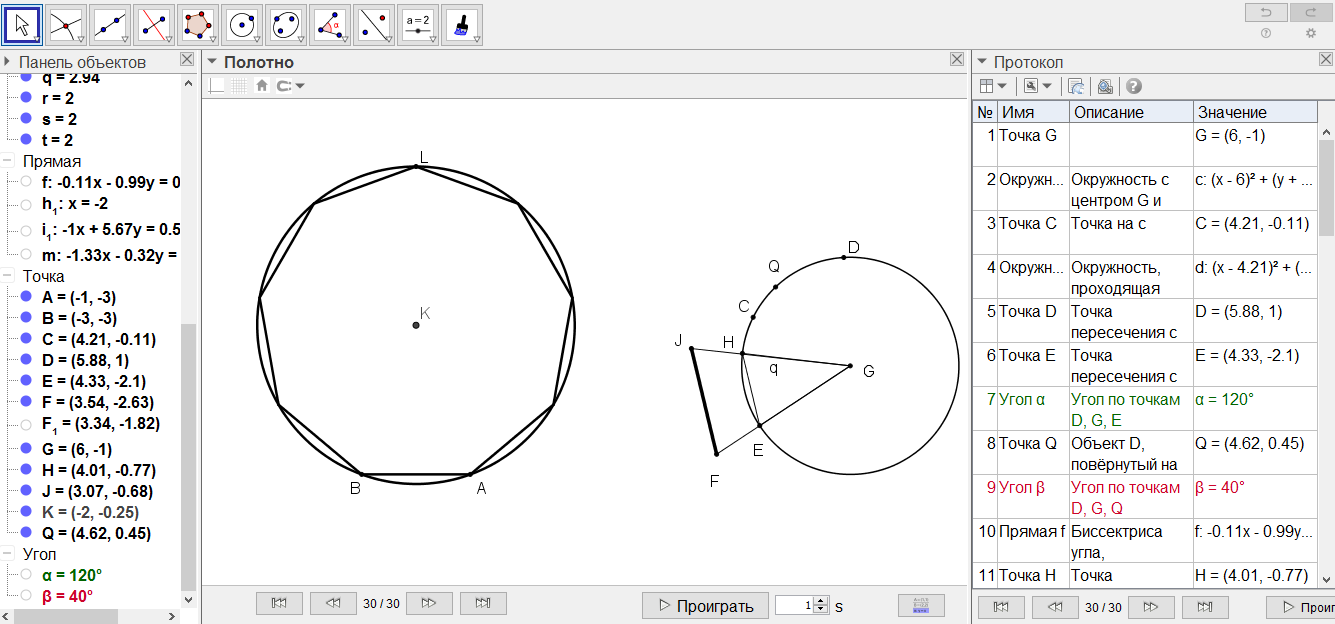
[56 - сурет]

Салудың алгоритмі:

1-қадам. Центрі G нүктесі етіп алып кезкелген w1 шеңберін сызамыз.

2-қадам. w1 шеңберінің бойынан C нүктесін белгілейміз.

3-қадам. C нүктесінен ұзындығы w1 шеңберінің радиусына тең CD және CE хордаларын жүргіземіз, яғни CD=R_w1, CE=R_w1.

4-қадам. CD доғасын тең үш бөлікке бөлетіндей, GK және GH сәулелерін жүргіземіз. 

5-қадам. GK және GE сәулелерін IF=AB болатындай етіп созамыз(18-сурет).

6-қадам. Центрлері A және B нүктелері, ал радиустары GI кесіндісіне тең болатын w2, w3 шеңберлерін сызып, олардың қыйылысу нүктесін O деп аламыз.

7-қадам. O нүктесін центрі етіп алып, радиусы OA кесіндісіне тең болатын w4 шеңберін сызамыз.

8-қадам. AB кесіндісінің ортасы арқылы өтетін перпендикуляр жүргізіп, оның w4 шеңберімен қыйылысу нүктесін L деп аламыз.

9-қадам. ALB доғасын теңдей сегіз бөлікке бөліп, оларды хордалармен қосамыз.

Математикалық негіздеме: Берілген алгоритмнің үшінші қадамы бойынша алынған CD және CE  кесінділері w1 шеңберінің радиусына тең болғандықтан CDG үшбұрышы мен GEG үшбұрышы тең қабырғалы үшбұрыштар. Ал, тең қабырғалы үшбұрыштың ішкі бұрыштары 60⁰ тең болатынын ескерсек, DE доғасы 120⁰-тық доға. Демек, бұл доға w1 шеңберінің үштен бір бөлігі. Төртінші қадам бойынша алынған KE кесіндісі w1 шеңберіне іштей сызылған дұрыс тоғызбұрыштың бір қабырғасы болып табылады, себебі KE доғасы DE  доғасының үштен бір бөлігі. IF кесіндісі KE кесіндісін параллел көшіру арқылы алынған бастапқы берілген кесіндіге тең кесінді болғандықтан, ол радиусы GI кесіндісіне тең болатын шеңберге іштей сызылған дұрыс тоғызбұрыштың қабырғасы болып табылады. Ал, шеңберді қандай да бір бөлікке бөліп тұрған доғаға сәйкес хорда сызылып тұрса, онда қабырғасының саны сол бөлік санына сәйкес дұрыс көпбұрыштың салынатынын ескерсек, берілген алгоритм бойынша салынға тоғызбұрышты дұрыс тоғызбұрыш деп атауға болады.

[X] Он бұрышты салу туралы. Егер ол АВ сызығына он бұрышты қалай тұрғызу керек десе, онда АВ сызығын С нүктесінде қақ бөліп В нүктесіне АВ сызығына тең ВD перпендикулярын орнатамыз. С нүктесін центр ретінде қабылдап АВ сызығында CD қашықтықта Е-ні белгілейміз. Ары қарай А мен В нүктелерінің әрқайсысынан центрлер ретінде АЕ қашықтықта G нүктесінде қиылысатын екі доға сызайық. G нүктесін қабырғасы АВ сызығы болып келген он бұрышқа  іштей сызылған дөңгелектің центрі ретінде қабылдаймыз. Ендеше, егер біз G центрі бар AG қашықтықта ABHF дөңгелегін сызып алып, AG мен GB сызықтарын олардың бағыттарында дөңгелектің шеңберіне дейін F пен H нүктелеріне дейін созсақ, АН пен BF доғаларын тең төрт бөлікке бөліп хордалармен қоссақ, онда тең қабырғалы және тең бұрышты он бұрышты аламыз³¹. Міне оның суреті [57 - сурет].

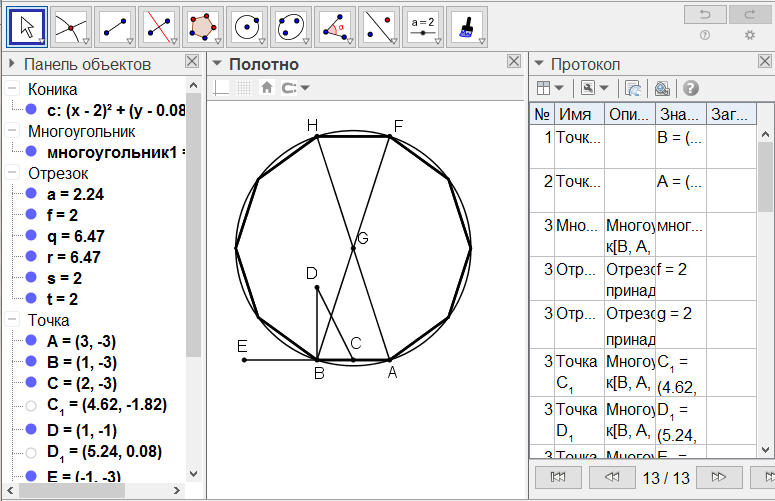
[57 - сурет]

Салудың алгоритмі: Егер ол АВ сызығына он бұрышты қалай тұрғызу керек десе, онда

1.     АВ сызығын С нүктесінде қақ бөлеміз

2.     В нүктесіне АВ сызығына тең ВD перпендикулярын орнатамыз.

3.     С нүктесін центр ретінде қабылдап АВ сызығында CD қашықтықта Е-ні белгілейміз.

4.     Ары қарай А мен В нүктелерінің әрқайсысынан центрлер ретінде АЕ қашықтықта G нүктесінде қиылысатын екі доға сызамыз.

5.     G нүктесін қабырғасы АВ сызығы болып келген он бұрышқа  іштей сызылған дөңгелектің центрі ретінде қабылдаймыз.

6.     Центрі G болатын AG қашықтықта ABHF дөңгелегін сызамыз

7.     AG мен GB сызықтарын олардың бағыттарында дөңгелектің шеңберіне дейін F пен H нүктелеріне дейін созамыз

8.     АН пен BF доғаларын тең төрт бөлікке бөліп хордалармен қоссақ, онда тең қабырғалы және тең бұрышты он бұрышты аламыз³¹.

Математикалық негіздеу:

Дұрыс онбұрышқа сырттай сызылған шеңбердің радиусы 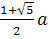 екендігі белгілі. Ал, берілген алгоритм бойынша AB қабырғасын 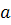-ға тең деп алсақ,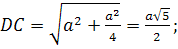 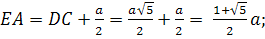    Яғни, EA=R  болып табылады. Бізге дәлелдеу керегі де осы.

[ХІ] Егер ол АВ сызығына тең циркуль ашасымен ғана, АВ сызығына тең қабырғалы тең бұрышты он бұрышты тұрғызу керек десе, онда оған жоғарыда төртінші ұсыныста көрсетілгендей бесбұрыштың үшбұрышын тұрғызамыз. G нүктесі АВ сызығына қарсы жатқан бұрыштың [төбесі] болсын. A және G, B және G сызықтарын қосамыз. G нүктесін  центр ретінде қабылдап, АВ қашықтықта CDFH дөңгелегін сызайық. AG, BG сызықтарын олардың бағытында дөңгелектің шеңберіне дейін [F және C нүктелеріне дейін] созайық. HF және DC доғаларының әрқайсысын тең төрт бөлікке бөліп, FI, IK, KM, MH, CL, LN, NX, XD бөліктерін аламыз. GF, GI, GK, GM, [GL], GN, GX, [GC], GH сызықтарын жүргіземіз де CDH дөңгелегінің центрінен шығатын осы сызықтардың әрқайсысында AD сызығына тең сызықтарды қосамыз. Бұл соңында О тұрған сызықтар. Оларды өзара және А мен В нүктелерімен түзу сызықтармен қосайық. Тең қабырғалы тең бұрышты АВО³² шығады. Міне оның суреті [58 - сурет].

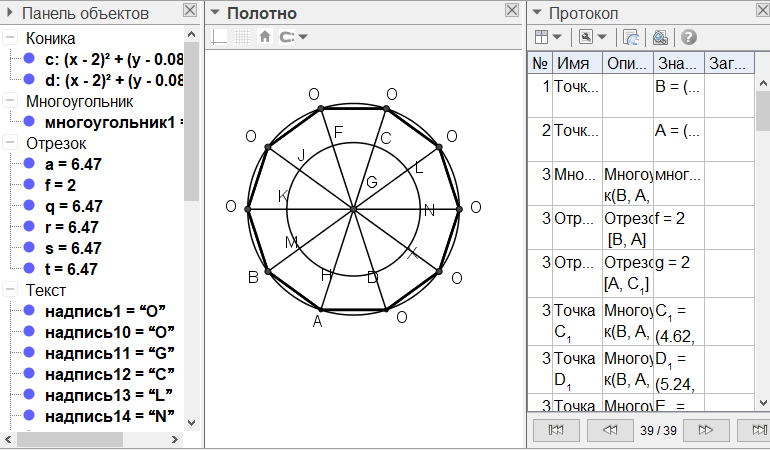
[58 - сурет]

Салудың алгоритмі: Егер ол АВ сызығына тең циркуль ашасымен ғана, АВ сызығына тең қабырғалы тең бұрышты он бұрышты тұрғызу керек десе, онда

1.     Жоғарыда төртінші ұсыныста көрсетілгендей бесбұрыштың үшбұрышын тұрғызамыз.

2.     G нүктесі АВ сызығына қарсы жатқан бұрыштың [төбесі] болсын деп алып, A және G, B және G сызықтарын қосамыз.

3.     G нүктесін центр ретінде қабылдап, АВ қашықтықта CDFH дөңгелегін сызамыз.

4.     AG, BG сызықтарын олардың бағытында дөңгелектің шеңберіне дейін [F және C нүктелеріне дейін] созамыз.

5.     HF және DC доғаларының әрқайсысын тең төрт бөлікке бөліп, FI, IK, KM, MH, CL, LN, NX, XD бөліктерін аламыз.

6.     GF, GI, GK, GM, [GL], GN, GX, [GC], GH сызықтарын жүргіземіз де CDH дөңгелегінің центрінен шығатын осы сызықтардың әрқайсысында AD сызығына тең сызықтарды қосамыз.

7.     Бұл соңында О тұрған сызықтар. Оларды өзара және А мен В нүктелерімен түзу сызықтармен қосамыз. Сонда тең қабырғалы тең бұрышты АВО³² шығады.

Математикалық негіздеу:

Бұл салуда да алдыңғы есепте қарастырғанымыздай дұрыс онбұрышқа сырттай сызылған шеңбердің радиусы 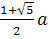 екендігіне сүйенеміз. Берілген алгоритм бойынша AB қабырғасын 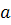-ға тең деп алсақ,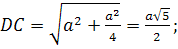 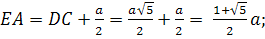      Яғни, EA=R  болып табылады. Бізге дәлелдеу керегі де осы.

АЛТЫНШЫ КІТАП

Кейбір фигураларға іштей басқа фигураларды салу  туралы.

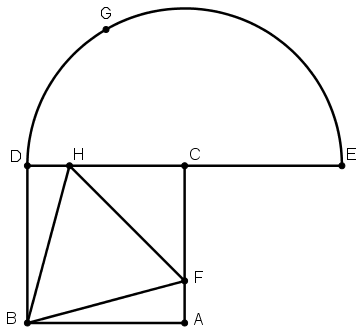
[I] Теңқабырғалы төртбұрышқа іштей үшбұрыш салу туралы. Егер ол теңқабырғалы төртбұрышқа іштей теңқабырғалы үшбұрышты қалай салу керек десе, онда ABCD шаршысын тұрғызамыз, DC сызығын Е нүктесіне дейін созамыз және CE-ні CD-ға тең қыламыз. ED сызығына жартышеңбер тұрғызамыз, D нүктесін центр ретінде алып DC қашықтықта G нүктесін белгілейміз. Ары қарай E нүктесін центр ретінде қабылдаймыз және EG қашықтықта H нүктесін белгілеп, DH-қа тең AF тұрғызып, B-мен F-ті, B-мен H-ты, F-пен H-ты қосамыз. ABCD шаршысына іштей  сызылған BFH теңқабырғалы үшбұрышын аламыз. Міне оның суреті [66- сурет].

[66- сурет].

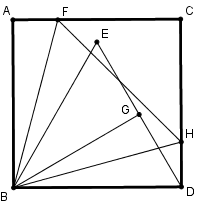
[IІ] Теңқабырғалы төртбұрышқа іштей үшбұрыш салудың екінші әдісі. Егер қаласақ, BD сызығында  BDE теңқабырғалы үшбұрышын тұрғызамыз, EBD бұрышын BG сызығымен қақ бөлеміз, AF сызығын  DH сызығына тең қыламыз, BH, BF және FH сызықтарын жүргіземіз, ABCD шаршысына іштей  сызылған теңқабырғалы және теңбұрышты BFH үшбұрышын аламыз. Міне оның суреті [67- сурет].

[67- сурет].

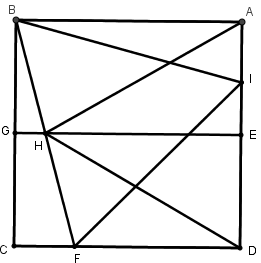
[IІІ] Теңқабырғалы төртбұрышқа іштей үшбұрыш салудың үшінші әдісі. Егер қаласақ, әрбір AD және BC сызықтарын E және G нүктелерінде қақ бөлеміз, EG –ні қосамыз,  A нүктесін центр ретінде аламыз және AB қашықтықта BH доғасын сызамыз. Екі еселенген GH сызығына тең  CF және AI сызықтарын саламыз. BI, BF және FI сызықтарын жүргіземіз; ABCD шаршысына іштей  сызылған теңқабырғалы BFI үшбұрышы пайда болады. Міне оның суреті [68- сурет].

[68- сурет].

[IV] Теңқабырғалы төртбұрышқа іштей үшбұрыш салудың төртінші әдісі. Шаршы салып, әрбір AD және BC сызықтарын E және H нүктелерінде қақ бөлеміз, EH–ты қосамыз,  B нүктесін центр ретінде аламыз және BC қашықтықта G нүктесін белгілейміз, EH сызығын GF сызығы GH сызығына тең болатындай, оның бағытында F нүктесіне дейін созамыз,  BF–ті қосамыз, ол AD сызығын K нүктесінде қияды. AK-ға тең CI-ді салып, BK, BI және IK сызықтарын жүргіземіз.  ABCD шаршысына іштей  сызылған теңқабырғалы BKI үшбұрышын аламыз. Міне оның суреті [69- сурет].

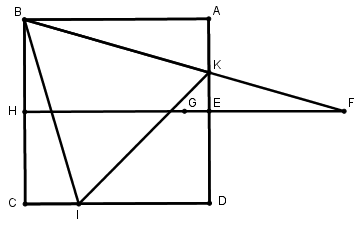
[69- сурет].

[V] Теңқабырғалы төртбұрышқа іштей үшбұрыш салудың бесінші әдісі. Егер біз осыны салғымыз келсе, ABCD шаршысына сырттай шеңбер сызамыз, оның центрі Е, BD диаметрін сызамыз, D нүктесін центр ретінде аламыз және DE қашықтықта H және G нүктелерін белгілейміз, BG және BH сызықтарын, F және I нүктелерінде қиылысатын  AD және DC сызықтарын жүргіземіз және FI-ді қосамыз.  ABCD шаршысына іштей  сызылған теңқабырғалы BFI үшбұрышын аламыз. Міне оның суреті [70- сурет].

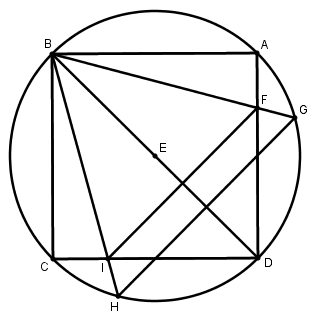
[70- сурет].

[VI] Шаршыға сырттай сызылған үшбұрыш салу туралы. Егер ол ABCD шаршысына сырттай теңқабырғалы үшбұрышты қалай салу керек десе, онда AB сызығына теңқабырғалы  ABE үшбұрышын тұрғызамыз, EA, EB сызықтарын олардың бағытында созамыз, сондай ақ  CD сызығын EA, EB сызықтарының жалғасымен G және H нүктелерінде қиылысқанға дейін созамыз. Сонда ABCD шаршысына сырттай  сызылған теңқабырғалы EGH үшбұрышын аламыз. Міне оның суреті [71- сурет].

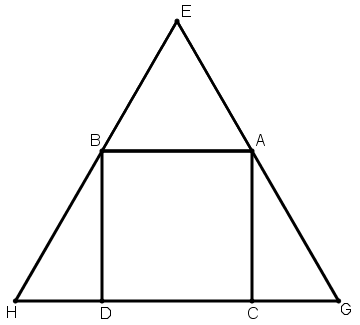
[71- сурет].

[VIІ] Үшбұрышқа сырттай сызылған шаршыны салу туралы. Егер ол теңқабырғалы үшбұрышқа сырттай теңқабырғалы және теңбұрышты төртбұрышты қалай салу керек десе, онда ABC теңқабырғалы  үшбұрышын тұрғызамыз, AC қабырғасын D нүктесінде қақ бөлеміз, BD сызығын E-ге дейін созамыз, DE сызығын AD-ға тең қылып аламыз, E мен A-ны, E мен C-ны қосамыз, EA және EH сызықтарына B нүктесінен BG және BH перпендикулярларын түсіреміз. Теңқабырғалы үшбұрышқа сырттай сызылған BGEH теңқабырғалы және теңбұрышты төртбұрышын аламыз. Міне оның суреті [72- сурет].

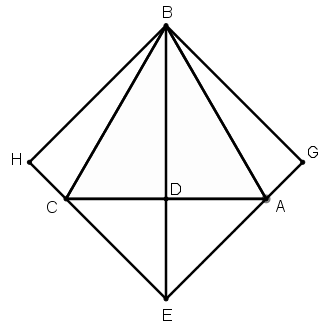
[72- сурет].

[VIІІ] Теңқабырғалы емес үшбұрышқа сырттай шаршы салу туралы. Егер ол қабырғалары әр түрлі ABC үшбұрышына сырттай теңқабырғалы және теңбұрышты қалай салу керек десе, онда С нүктесінен CA сызығына CD перпендикулярын түсіреміз, оны осы сызыққа тең етіп, D- мен B-ны қосамыз және DB-ны оның бағытында созамыз, CE-ға С нүктесінен CG перпендикулярын жүргіземіз, A нүктесінен CE-ға параллель сызық жүргіземіз, бұл HA сызығы. Қабырғалары әр түрлі ABC үшбұрышына сырттай теңқабырғалы және теңбұрышты HGCE төртбұрышын аламыз. Міне оның суреті [73- сурет].

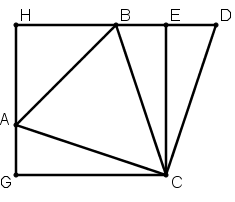
[73- сурет].

[ІX] Үшбұрышқа сырттай сызылған шаршыны салудың екінші тәсілі. Егер ол қабырғалары әр түрлі ABC үшбұрышына сырттай теңқабырғалы және теңбұрышты шаршыны қалай салу керек десе, онда С нүктесінен CA сызығына CD перпендикулярын түсіреміз, оны осы сызыққа тең етіп, D- мен B-ны қосамыз және DB-ны оның бағытында созамыз, CE-ға С нүктесінен CG перпендикулярын жүргіземіз, A нүктесінен CE-ға параллель сызық жүргіземіз, бұл HA сызығы. Қабырғалары әр түрлі ABC үшбұрышына сырттай теңқабырғалы және теңбұрышты HGCE төртбұрышын аламыз. Міне оның суреті [74- сурет].

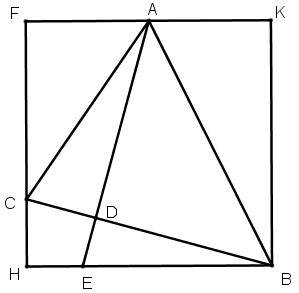
[74- сурет].

[X] Үшбұрышқа сырттай сызылған шаршыны салудың үшінші тәсілі. Егер қаласақ, АВ қабырғасына тең қылып, А нүктесінен АВ сызығына AD перпендикулярын түсіреміз. АВС үшбұрышына тең ADE үшбұрышын тұрғызамыз. Сонда DE  BC-ға тең, ал AE  AC-ға тең. ЕВ қосамыз және С нүктесінен ЕВ сызығында СН перпендикулярын түсіреміз, ал А нүктесінен ЕВ және СН сызықтарында AF және AG перпендикулярларын түсіреміз. Сонда AGHF- шаршы болады. Міне оның суреті [75- сурет].

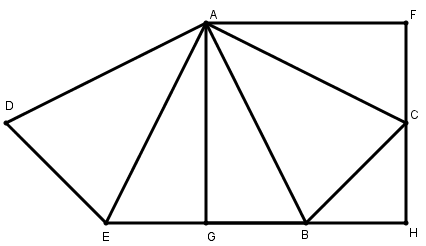
[75- сурет].

[XІ] Үшбұрышқа іштей сызылған шаршыны салу туралы. Егер ол ABC үшбұрышына іштей теңқабырғалы және теңбұрышты шаршыны қалай салу керек десе, онда В нүктесінен ВС сызығына тең BD перпендикулярын тұрғызамыз және AD –мен қосамыз;  AD сызығы BC-мен Е нүктесінде қиылысады. Е нүктесінен ЕВ сызығына EG перпендикулярын тұрғызамыз, ол АВ сызығымен G нүктесінде қиылысады. G нүктесінен ВС сызығына параллель GH сызығын жүргіземіз және  H нүктесінен ВC сызығына HF перпендикулярын түсіреміз. Сонда ABC үшбұрышына іштей сызылған теңқабырғалы және теңбұрышты EGHF төртбұрышы пайда болады. Міне оның суреті [76- сурет].

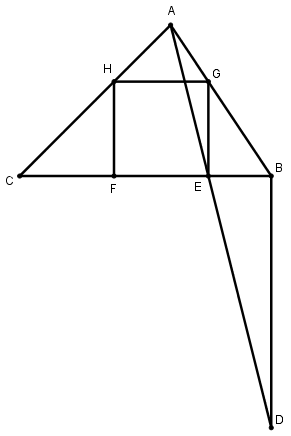
[76- сурет].

[XІІ] Үшбұрышқа іштей сызылған шаршыны салудың екінші әдісі. ВС сызығына тең болатындай В нүктесінен BD перпендикулярын түсіреміз. А нүктесінен АЕ перпендикулярын түсіреміз, D мен Е-ны қосамыз, DE АВ сызығымен G нүктесінде қиылысады;  G нүктесінен ВС сызығына параллель болатын GH сызығын жүргіземіз және ВС сызығына GF және HI перпендикулярларын түсіреміз, сонда ABC үшбұрышына іштей сызылған теңқабырғалы және теңбұрышты GHIF төртбұрышы аламыз. Міне оның суреті [77- сурет].

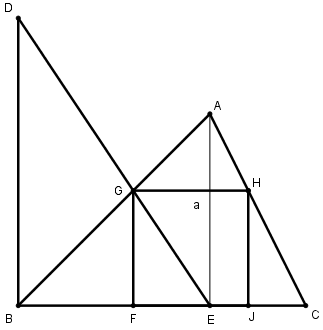
[77- сурет].

[XІІІ] Теңқабырғалы үшбұрышқа іштей сызылған шаршыны салу туралы. Егер қаласақ ВС-да BDEC шаршысын тұрғызамыз,  G нүктесінде ВС сызығын қақ бөлеміз, DG және EG сызықтарын жүргіземіз, олар АВ және АС сызықтарымен H және F нүктелерінде қиылысады, H-ты F-пен қосамыз. Одан HK және FL перпендикулярларын түсіреміз, сонда ABC үшбұрышына іштей сызылған шаршы аламыз. Міне оның суреті [78 және 79- суреттер].

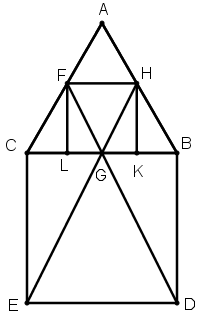
[78- сурет].

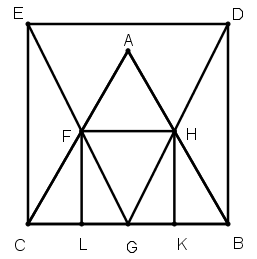
[79- сурет].

[XІV] Қабырғалары әр түрлі үшбұрышқа іштей теңқабырғалы үшбұрыш салу туралы. Егер ол бір қабырғасы ВС сызығына параллель қабырғалары әр түрлі АВС үшбұрышына іштей теңқабырғалы үшбұрышты қалай тұрғызамыз десе, онда ВС сызығында BDC теңқабырғалы үшбұрышын тұрғызамыз, AI және DE перпендикулярларын тұрғызамыз, В нүктесінен BC-ға BG перпендикулярын түсіреміз, BH сызығын AI сызығына тең етеміз, ал HG сызығын DE перпендикулярына тең етіп аламыз. С-мен G-ді қосып, H нүктесінен GC сызығына параллель HF сызығын жүргіземіз, сонда BF сызығы бір қабырғасы ВС сызығына параллель және қарсы жатқан бұрыштың төбесі BC-да жататын АВС үшбұрышына іштей сызылған үшбұрыштың қабырғасы. 

Сондықтан егер біз  ABC үшбұрышында BC-ға параллель және BF-ға тең LN сызығын жүргізіп, L нүктесін центр ретінде қабылдаймыз және LN қашықтықта ВС сызығынан М нүктесін белгілесек, онда ABC үшбұрышына  іштей сызылған теңқабырғалы LMN үшбұрышын аламыз. Міне оның суреті [80 сурет].

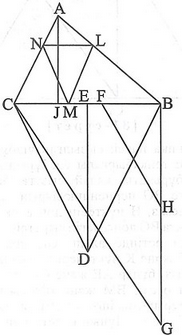
[80 сурет].

[XV] Қабырғалары әр түрлі үшбұрышқа сырттай теңқабырғалы үшбұрыш салу туралы. Егер ол қабырғалары әр түрлі АВС үшбұрышына сырттай теңқабырғалы үшбұрышты қалай саламыз десе, онда ВС сызығына параллель сызық жүргіземіз, ВС сызығында қабырғалары әр түрлі BDC үшбұрышын тұрғызамыз, DB және DC сызықтарын өз бағыттарында созамыз да, А нүктесінен ВС сызығына параллель және DB мен DC сызықтарын E және G нүктелерінде қиятын GAE сызығын жүргіземіз. Сонда теңқабырғалы DEG үшбұрышын аламыз. Міне оның суреті [81 сурет].

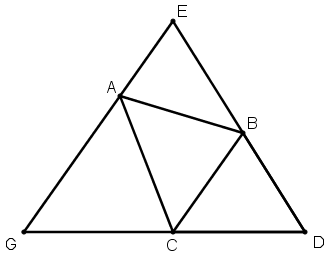
[81 сурет].

[XVI] Бесбұрышқа іштей үшбұрыш салу туралы. Егер ол теңқабырғалы АВСDE бесбұрышына іштей теңқабырғалы үшбұрышты қалай саламыз десе, онда В нүктесінен DE-ге BG перпендикулярын тұрғызамыз, оны H нүктесінде қақ бөлеміз, H нүктесін центр ретінде қабылдап HB қашықтықта BG шеңберін сызамыз. G нүктесін центр ретінде қабылдаймыз және GH қашықтықта шеңбердің бойынан F және K нүктелерін белгілейміз. BK және KF сызықтарын жүргіземіз, олар AE және CD сызықтарын M және N нүктелерінде қияды, BM, BN және MN сызықтарын жүргіземіз. ABCDE бесбұрышына іштей сызылған теңқабырғалы BMN үшбұрышы пайда болады. Міне оның суреті [82 сурет].

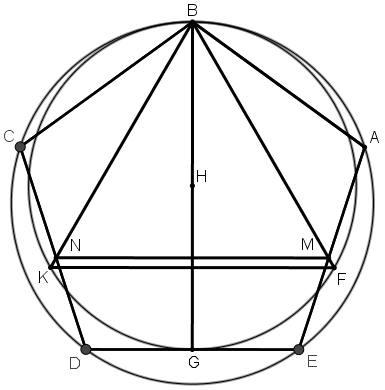
[82 сурет].

[XVIІ] Бесбұрышқа сырттай сызылған үшбұрыш салу туралы. Егер ол теңқабырғалы АВСDE бесбұрышына сырттай теңқабырғалы және теңбұрышты үшбұрышты қалай саламыз десе, онда бесбұрышқа іштей теңқабырғалы үшбұрыш саламыз, бұл BGH үшбұрышы, А және С нүктелерінен BG және BH сызықтарына параллель FL және FK екі түзу сызықтарын жүргіземіз, DE сызығын оның екі бағытымен L және K нүктелеріне дейін созамыз. ABCDE бесбұрышына сырттай сызылған теңқабырғалы FLK үшбұрышын алдық. Міне оның суреті [83 сурет].

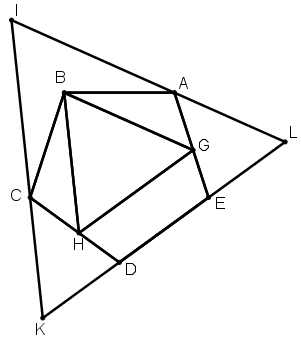
[83 сурет].

[XVIIІ] Бесбұрышқа іштей шаршы салу туралы. Егер ол теңқабырғалы және теңбұрышты АВСDE бесбұрышына іштей теңқабырғалы және теңбұрышты төртбұрышты қалай саламыз десе, онда С нүктесінен АЕ сызығына CG перпендикулярын түсіреміз, оны H нүктесінде қақ бөлеміз де, ол арқылы АЕ сызығына параллель FHK сызығын жүргіземіз және C мен F, C мен K,  K мен G, G мен F нүктелерін сызықтармен қосамыз. ABCDE бесбұрышына іштей сызылған теңқабырғалы және теңбұрышты CFGK төртбұрышын аламыз. Міне оның суреті [84 сурет].

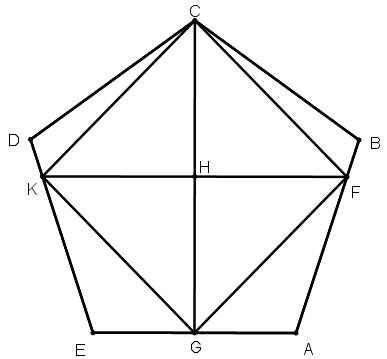
[84 сурет].

[XІX] Бесбұрышқа сырттай шаршы салу туралы. Егер ол теңқабырғалы АВСDE бесбұрышына сырттай теңқабырғалы және теңбұрышты төртбұрышты қалай саламыз десе, онда АЕ сызығын G нүктесінде қақ бөлеміз де, СЕ сызығына тең болатындай GH перпендикулярын тұрғызамыз, H пен E-ні, H-пен A-ны қосамыз да, өз бағыттарында жалғастырып сызамыз, B және D нүктелерінен HF және HL сызықтарына BF және DL перпендикулярларын түсіреміз де, оларды K нүктесіне дейін өз бағыттарында созамыз, сонда ABCDE бесбұрышына сырттай сызылған теңқабырғалы және теңбұрышты FKLH төртбұрышын аламыз. Міне оның суреті [85 сурет].

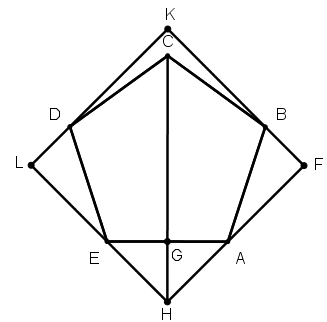
[85 сурет].

[XX] Шаршыға іштей сызылған бесбұрыш салу туралы. Егер ол АВСD шаршысының диагоналында іштей E бұрышты қалаған шамадағы EGHFI бесбұрышына ұқсас теңқабырғалы және теңбұрышты бесбұрышты қалай саламыз десе, онда қалаған шамадағы KLMNX теңқабырғалы бесбұрышын тұрғызамыз және оның маңайына шаршы тұрғызамыз. Оның қабырғаларының бірі- ZQ болсын. ZO сызығын жүргіземіз, AB қабырғасына тең болатындай QP аламыз, P нүктесінен ZO сызығына параллель PG сызығын жүргіземіз, ал R нүктесінен MN қабырғасының  ортасы мен Q нүктесі арқылы өтетін сызық жүргіземіз. АС қосамыз, QR сызығына тең CS белгілейміз, АС сызығына перпендикуляр HSF түруін жүргіземіз. Содан соң H және F нүктелерін центр етіп алып HF қашықтықта AB және AD сызықтарының бойынан G және I нүктелерін белгілейміз. G және I нүктелерін центр етіп алып GH қашықтықта E нүктесін белгілейміз де, HG, GE, EI және IE сызықтарын жүргізіп ABCD шаршысына іштей сызылған EGHFI теңқабырғалы және тең бұрышты бесбұрышын аламыз⁴⁸. Міне оның суреті [86 сурет].

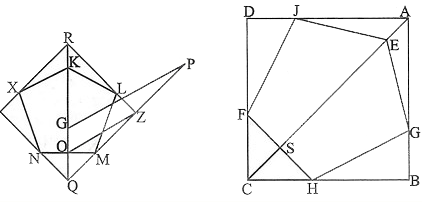
[86 сурет].

[XXI] Шаршыға іштей сызылған сегізбұрыш салу туралы. Егер ол теңқабырғалы және теңбұрышты сегізбұрышты қалай саламыз десе, онда ABCD  шаршысын тұрғызамыз, Е нүктесінде қиылысатын диаметрлерін жүргіземіз, Е нүктесін центр етіп алып шаршының қабырғасының жартысына тең қашықтықта G нүктесін белгілейміз,  G нүктесін центр ретінде алып, D және G нүктелері қашықтығында H пен F нүктелерін белгілейміз, шаршының қабврғаларының әрбір бұрышынан DF және DH-қа тең сызықтар белгілейміз. Бұл MA, AL, BN, BX, CK, CI сызықтары. HF, IK, LM және NX сызықтарын қосамыз. IKLMNXHF теңқабырғалы және теңбұрышты сегізбұрышты пайда болды. Міне оның суреті [87 сурет].

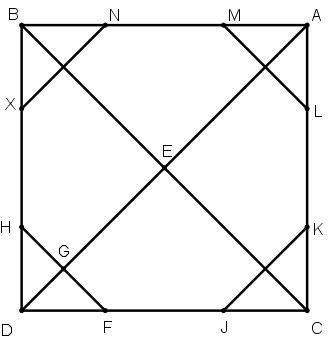
[87 сурет].

[XXIІ] Шаршыға іштей сызылған сегізбұрыш салудың басқа әдісі. Егер қаласақ циркульдің ашасымен шаршы диагоналінің жартысындай яғни AE қашықтықта шаршының әрбір бұрышынан M, N, X, H, F, I, K және L нүктелерін белгілейміз де, LM, NX, HF және IK сызықтарын жүргіземіз.  Теңқабырғалы және теңбұрышты LMNXHFIK сегізбұрышты пайда болады. Міне оның суреті [88 сурет].

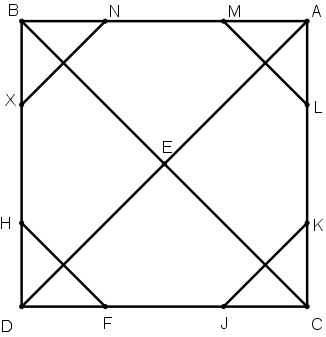
[88 сурет].

[XXIІІ] Сегізбұрышқа сырттай сызылғаншаршы салу туралы. Егер ол теңқабырғалы ABCDEGHF сегізбұрышына сырттай шаршыны қалай саламыз десе, онда AB, CD, EG, HF сызықтарын I, K, L, M нүктелерінде қиылысқанша созамыз. Сонда ABCDEGHF сегізбұрышына сырттай сызылған теңқабырғалы және теңбұрышты IKLM төртбұрышын аламыз. Міне оның суреті [89 сурет].

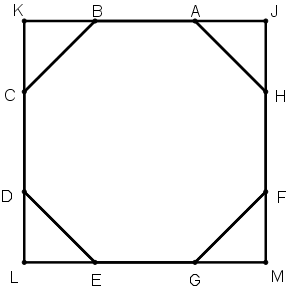
[89 сурет].

БЕСІНШІ КІТАП

Фигураларға іштей шеңбер салу туралы.

[І]  Егер ол ABC үшбұрышына іштей қалай шеңбер сызу керек десе, онда В нүктесін центр етіп алып, АВ және ВС сызықтарында D және E [нүктелерін] белгілейміз. Осы [нүктелердің] әрқайсысын центр етіп қабылдап G нүктесінде қиылысатын екі шеңбер [тұрғызамыз] да, BG сызығын жүргіземіз. Ары қарай С нүктесін центр етіп аламыз және  АС және СВ сызықтарының бойынан H және F [нүктелерін] белгілейміз;  H және F нүктелерін центр етіп алып, I нүктесінде қиылысатын екі шеңбер [тұрғызамыз] да, I және С-ны қосамыз. CI сызығы BG сызығымен K нүктесінде қиылысады.   АВС⁴⁷ үшбұрышына іштей сызылған шеңбердің центрі K – нүктесін аламыз. Міне оның суреті [65- сурет].

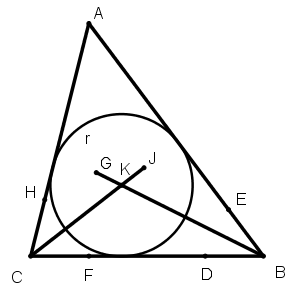
[65- сурет].

[II] Осындай әдіспен басқа да тең қабырғалы және тең бұрышты фигураларға іштей шеңбер сызуға болады: оның екі бұрышын қақ бөлеміз. Сызықтардың қиылысуы үшбұрышқа [төртбұрышқы, бесбұрышқы және т.с.с] іштей сызылған шеңбердің центрін береді.

Қолөнершілер шеңберге іштей сызылған және сырттай сызылған фигураларды шеңберді қалауынша [тең] бөліктерге бөлу арқылы тұрғызатындығын біліп қой.  Мысалы шеңберге іштей сызылған бесбұрышты салу үшін оны тең бес бөлікке бөліп, бөлу орындарын қосады және бөлу орындарынан шеңберді жанап өтетін сызықтар жүргізеді де, сонымен тең қабырғалы, тең бұрышты іштей сызылған бесбұрыш және сырттай сызылған [сондай бесбұрыш] тұрғызады. Бұл салу алтыбұрыш үшін тіпті ысылмаған қолөнерші үшін күрделі емес. Жақсы өнер жасау үшін қолөнерші осы тарауды біздің дәлелдегендерімізге сәйкес бесбұрыш, алтыбұрыш, онбұрыш, тағы басқа фигуралардың қабырғаларына [тең қашықтықта] қосылған бірнеше таңбаларды айналдыра ұрғылап [салады]. Циркульді көп рет ашып жауып қозғалта бөлуді іске асыратындар тілегіне тек үлкен еңбекпен жуықтап қана жетеді. Егер сіз біз көрсеткендей бұл фигуралардың қабырғаларын анықтауда белгілі өнер жолына кіріссеңіз онда білгін, егер сен осы фигуралардың біреуінің шеңберге іштей сызылғанын салсаң және осы фигураны салуың дұрыс болса, онда егер сен бөлу орындарынан шеңберді жанап өтетін сызықтар жүргізсең сызбада оны сырттай салған фигура шығады³³.  Фигураларға сырттай сызылған және оларға іштей сызылған шеңберлер жайында айтсақ, онда олар алуан түрлі, ал бұл кітапта  олардың әрқайсысы туралы оларды қалай салу керектігі дәлелденген³³.

[І] Шеңберге іштей салынған үшбұрышты салу. Егер біз шеңберге іштей сызылған теңқабырғалы үшбұрышты салғымыз келсе, онда центрі D нүктесінде болатын АВС шеңберін салып, оның ішіне ADE диаметрін жүргіземіз, Е нүктесін центр етіп қабылдаймыз да ED қашықтықта В мен С нүктелерін белгілеп, АВ, АС және ВС сызықтарын жүргіземіз. Сонда теңқабырғалы АВС үшбұрышын аламыз³⁴. Міне оның суреті [45 сурет].

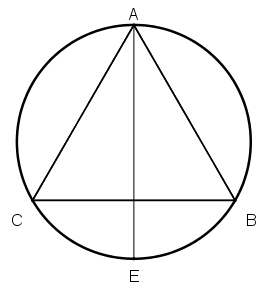
[45 сурет].

[ІІ] Шеңберге сырттай сызылған үшбұрышты салу. Егер біз шеңберге сырттай сызылған теңқабырғалы үшбұрышты салғымыз келсе, онда оның ішіне теңқабырғалы АВС үшбұрышын сызамыз да, А, В және С нүктелерінің әрқайсысынан G, H және F нүктелерінде кездескенге дейін жанама сызықтар жүргіземіз. Сонда теңқабырғалы HGF³⁵ үшбұрышын аламыз. Міне оның суреті [46 сурет].

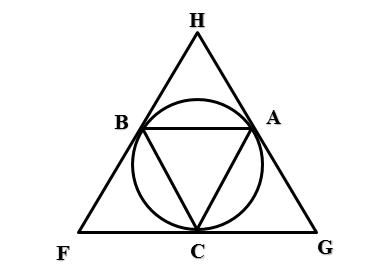
[46 сурет].

[ІІІ] Шеңберге іштей сызылған шаршыны салу. Егер ол шеңберге іштей сызылған теңқабырғалы және тең бұрышты төртбұрышты қалай салу керек десе, онда AB[C]D шеңберін тұрғызып оның ішіне тік бұрыш бойынша қиылысатын АС және ВD диаметрлерін саламыз да AB, BC, CD және DA сызықтарын жүргіземіз. Сонда теңқабырғалы және тең бұрышты ABCD³⁶ төртбұрышын аламыз. Міне оның суреті [47 сурет].

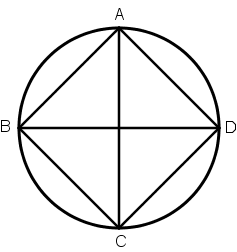
[47 сурет].

[ІV] Егер ол ABCD шеңберінің жарты диаметріне тең циркуль ашасын пайдаланып теңқабырғалы және тең бұрышты төртбұрышты шеңберге іштей қалай салу керек десе, онда АС диаметрін жүргіземіз. А нүктесін центр ретінде қабылдап циркуль ашасымен Е және G нүктелерін белгілейік та, Е мен G-ді қосайық. С нүктесін центр ретінде қабылдап АЕ қашықтықта H пен F-ті белгілейміз де H пен F-ті қосамыз. KG және IF сызықтарын жүргізейік, олар М нүктесінде қиылысады. М нүктесімен центрді қосып осы сызықты оның В мен D нүктелеріне дейінгі бағытында созайық. AB, BC, CD және DA сызықтарын жүргіземіз. Теңқабырғалы және тең бұрышты ABCD³⁷ төртбұрышы шығады. Міне оның суреті [48 сурет].

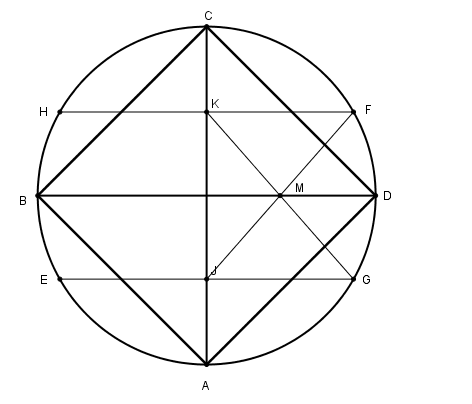
[48 сурет].

[V] Егер қаласаңыз А және С нүктелерін центр ретінде қабылдап Е,G,H және F нүктелерін белгілейік. АС сызығын I және К нүктелерінде қиып өтетін EG және HF сызықтарын жүргізейік. Центрлері осы нүктелер болатын циркульдің ашасындай қашықтықта L және М нүктелерінде қиып өтетін екі шеңбер сызайық. L және М-ді өзара қосайық та [LM]-ді В мен D нүктелеріне дейін созайық. AB, BC, CD және DA сызықтарын жүргізейік. Теңқабырғалы және тең бұрышты ABCD төртбұрышын аламыз. Міне оның суреті [49 сурет].

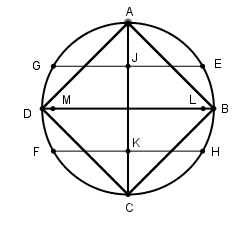
[49 сурет].

[VІ] Егер қаласаңыз Е,G,H және F нүктелерін центр ретінде қабылдап, I және К нүктелерін қилысатын шеңберлер салайық. IК сызығын жүргізейік, ол шеңберді В және D нүктелерінде қиып өтеді. Теңқабырғалы және тең бұрышты ABCD төртбұрышын аламыз. Міне оның суреті [50 сурет].

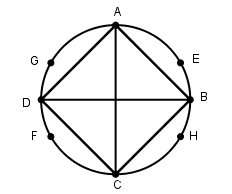
[50 сурет].

[VІІ] Егер қаласаңыз А,F және C,G нүктелерін қосайық. А,F және C,G нүктелерін қосатын сызықтар М нүктесінде қиылысады. Оны центрмен қосып ол сызықты B мен D нүктелеріне дейін созайық. Міне оның суреті [51 сурет].

[51 сурет].

[VІІІ] Шеңберге іштей сызылған бесбұрышты салу. Егер ол ABCD шеңберіне іштей сызылған тең қабырғалы және тең бұрышты бесбұрышты қалай салу керек десе онда D нүктесін центр ретінде алып онда ADC диаметрін жүргіземіз де D нүктесіне  DB перпендикулярын орнатамыз. AD-ны Е нүктесінде қақ бөліп Е нүктесін центр ретінде алып ЕВ қашықтықта G нүктесін белгілейік те В нүктесін центр ретінде алып ВG қашықтықта F нүктесін белгілейік. Сонда шеңбердің бестен бір бөлігі BF доғасын аламыз. IF, IK, KH және HB доғаларын BF доғасына тең ете жүргізіп FB, BH, HK, KI, IF сызықтарын сызамыз. Сонда тең қабырғалы және тең бұрышты BFIKH³⁸ бесбұрышын аламыз. Міне оның суреті [52 сурет].

[52 сурет].

[IX] Егер ол ABC шеңберіне іштей тең қабырғалы және тең бұрышты бесбұрышын егер D – шеңбер центрі болса және  ашасы жарты диаметрге тең циркулмен қалай салу керек десе,  онда DA сызығына AB сызығына бесбұрыш салу кезінде салынған үшбұрышты  салайық. Бұл ADG  үшбұрышы болсын, ол ABC шеңберін C нүктесінде қияды. ABC доғасын B, H, E және C нүктелерінде төрт тең бөлікке бөліп, AC, CE, EH, HB және BA сызықтарын жүргізейік. Сонда тең қабырғалы және тең бұрышты ACEHBA³⁹ бесбұрышын аламыз. Міне оның суреті [53-сурет].

[53-сурет].

         [X] Шеңберге іштей салынған бесбұрышты салудың басқа жолы. DA сызығына DA сызығына тең AE перпендикулярын тұрғызып, DA сызығын G нүктесінде қақ бөлейік, GE жүргізіп, AD сызығына тең GH сызығын салайық, оны F нүктесінде қақ бөліп, DA-ны I нүктесінде қиятын FI перпендикулярын тұрғызайық. I нүктесін центр ретінде қабылдап, DA қашықтықта M және L белгілейік. Сонда ML доғасы – шеңбердің бестен бірі. Міне оның суреті [54-сурет].

[54-сурет].

         [XІ] Шеңберге іштей салынған алтыбұрышты салу. Егер ол шеңберге іштей салынған тең қабырғалы және тең бұрышты  алтыбұрышты қалай салу керек десе, онда A және C нүктелерінің әрқайсысын центр ретінде алып AC диаметрін жүргізіп, диаметрдің жартысына тең қашықтықта B және H, E және G белгілейік. AB, BE, EG, CG, GH және HA сызықтарын жүргізейік. Тең қабырғалы және тең бұрышты ABECGH⁴⁰ алтыбұрышын аламыз. Міне оның суреті [55-сурет].

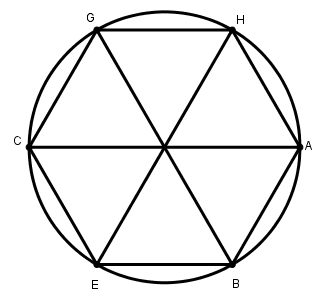
[55-сурет].

[XІІ] Шеңберге іштей салынған жетібұрышты салу. Егер ол шеңберге іштей салынған тең қабырғалы және тең бұрышты жетібұрышты қалай салу керек десе, онда ADC диаметрін жүргіземіз де, AD, яғни жарты диаметр қашықтықта B және E белгілеп, BE жүргізейік, ол AC сызығын G нүктесінде қияды. B нүктесін центр ретінде қабылдап, BG қашықтықта H нүктесін белгілейік. Сонда BH доғасы – шеңбердің дәл емес, жуық жетіден бірі. Сондықтан егер ABCE шеңберін BH доғасына тең бөліктерге бөліп, бөлу орындарын өз ара қоссақ, онда тең қабырғалы және тең бұрышты FBHIKLM⁴¹ жетібұрышын аламыз. Міне оның суреті [56-сурет].

[56-сурет].

          [XIІІ] Шеңберге іштей салынған сегізбұрышты салу. Егер ол шеңберге іштей салынған тең қабырғалы және тең бұрышты  сегізбұрышты қалай салу керек десе, онда оған тең қабырғалы және тең бұрышты  төртбұрышты іштей саламыз да, әр доғаны қақ бөліп, бөлу орындарын жаңа нүктелерде түзу сызықтармен қосамыз. Тең қабырғалы тең бұрышты да сегізбұрыш аламыз. Міне оның суреті [57-сурет].

[57-сурет].

           [XIV] Шеңберге іштей салынған тоғызбұрышты салу. Егер ол шеңберге іштей салынған [тең қабырғалы және тең бұрышты] тоғызбұрышты қалай салу керек десе,  шеңберге  тең қабырғалы   үшбұрышты іштей  салып, әр доғаны тең үш бөлікке бөлеміз де, бөлу орындарын түзу сызықтармен қосамыз.  Тең қабырғалы [тең бұрышты да] тоғызбұрыш аламыз. Міне оның суреті [58-сурет].

[58-сурет].

[XV] Шеңберге іштей салынған онбұрышты салу. Егер ол шеңберге іштей салынған онбұрышты қалай салу керек десе, онда егер қаласақ, оған іштей бесбұрыш салып, доғаның әрқайсысын қақ бөлеміз [де, бөлу нүктелерін сызықтармен қосамыз], іштей сызылған онбұрыш шығады. Егер қаласақ, алдыңғы салынғанға ұқсас іштей бесбұрыш саламыз да, сосын бұрынғыдай DG сызығын [саламыз]. Бұл онбұрыштың хордасы. Шеңберді DG сызығына тең бөліктерге бөлейік те, бөлу орындарын өз ара түзу сызықтармен қосайық. Шеңберге іштей салынған тең қабырғалы [тең бұрышты да] онбұрыш⁴² шығады. Міне оның суреті [59-сурет].

[59-сурет].

ТӨРТІНШІ КІТАП

Фигураларға сырттай шеңбер салу туралы.

[І]  Егер ол ABC үшбұрышына сырттай шеңбер сызу керек немесе бір сызықтың бойында жатпайтын әртүрлі үш нүкте арқылы шеңбер салу керек десе, онда бұл екі сұрақтың мағынасы бірдей. А және В нүктелерін центр ретінде қабылдап, D және E нүктелерінде қиылысатын екі шеңбер тұрғызамыз. DE сызығын жүргіземіз. Ары қарай А және С, сол сияқты А және В нүктелері арқылы G және H нүктелерінде қиылысатын екі шеңбер сызып, GH сызығын жүргіземіз. [GH сызығы] DE сызығымен F нүктесінде қиылысады. Сонда А, В және С⁴³ нүктелері арқылы өтетін шеңбердің центрі - F нүктесін аламыз. Міне оның суреті [60 сурет].

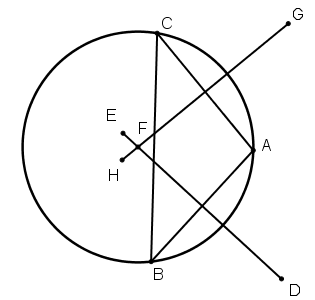
[60 сурет].

[ІІ] Үшбұрышқа сырттай сызылған шеңберді тұрғызудың екінші тәсілі. А және С нүктелерінен АВ және ВС сызықтарына AD және DC  перпендикулярларын тұрғызамыз; олар D нүктесінде қиылысады; BD жүргіземіз және оны Е нүктесінде қақ бөлеміз; Сонда Е - А, В және С нүктелері арқылы өтетін ізделінді шеңбердің центрі⁴³. Міне оның суреті [61 сурет].

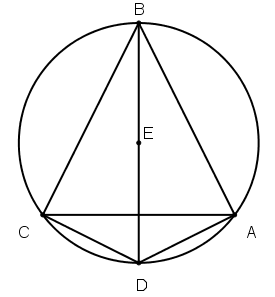
[61 сурет].

         [ІІІ] Шаршыға сырттай сызылған шеңбер жайлы. Егер ол ABCD шаршысына сырттай шеңберді қалай        сызу керек десе, он  да Е нүктесінде қиылысатын AC және BD диагональдарын жүргіземіз. Е - А, В, С және D⁴⁴ нүктелері арқылы өтетін шеңбердің центрі. Міне оның суреті [62 сурет].

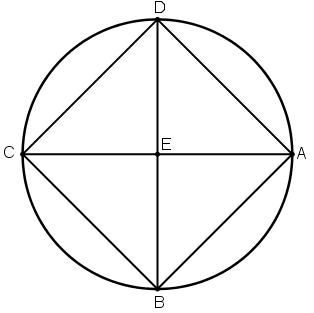
[62 сурет].

[ІV] Бесбұрышқа сырттай сызылған шеңберді тұрғызу жайлы. Егер ол ABCDE бесбұрышына сырттай шеңберді қалай тұрғызамыз десе, онда А және В нүктелерін центр етіп алып G және Н нүктесінлерінде қиылысатындай екі шеңбер тұрғызамыз да, GH сызығын жүргіземіз. Ары қарай дәл осындай  А және Е нүктелерін центр етіп алып I және K нүктесінлерінде қиылысатындай екі шеңбер тұрғызамыз. GH сызығымен L нүктесінде қиылысатындай IK [сызығын]  жүргіземіз. Сонда L - А, В, С, D, E⁴⁵ нүктелері арқылы өтетін шеңбердің центрі. Міне оның суреті [63   сурет].

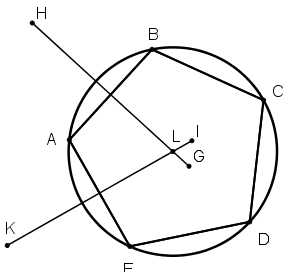
[63   сурет].

[V] Алтыбұрышқа сырттай сызылған шеңберді тұрғызу жайлы. Егер ол ABCDEG алтыбұрышына сырттай шеңберді қалай тұрғызамыз десе, онда А және В нүктелерінің әрқайсысын центр етіп алып АВ қашықтықта Н нүктесінде қиылысатындай екі шеңбер тұрғызамыз. Сонда H - А, В, С, D, E, G⁴⁶ нүктелері арқылы өтетін шеңбердің центрі. Міне оның суреті [64 сурет].

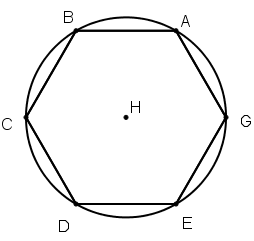
[64 сурет].

[VІ] Егер [теңқабырғалы] көпқабырғалы және көпбұрышты фигура берілсе, онда оған сырттай шеңбер салу үшін жоғарыда бесбұрышқа сырттай шеңбер салғанымыздай, қабырғаларын қақ бөліп перпендикулярлар тұрғызамыз. Бұл тұрғызылымның  бесбұрышқа сырттай шеңбер салудан еш айырмашылығы жоқ, қабырға саны көп немесе аз [фигуралар үшін].

         [I]О построении треугольника. Если он сказал: как построить на линии АВ равносторонний  треугольник, то из каждой из точек А и В как  из центров опишем на расстоянии АВ круги. Они пересекутся в точке С. Соединим точку С с точками А и В прямыми линиями СА и СВ. Получится равносторонний треугольник АВС. Вот рисунок этого [рис. 34].

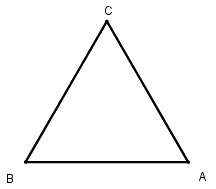
(рис 34)

 [II] О построении квадрата. Если он сказал: как построить на линии АВ равносторонний {и равноугольник} четырехугольнику, то восставим в каждой из точек А и В перпендикуляры, равные линии АВ; это - линии АС и ВD.  Соединив С и D, получим равносторонний {и равноугольник} четырехугольник АВСD. Вот рисунок этого [рис. 35].

[рис 35].

[III] О построении пятиугольника. Если он сказал: как построить на линии АВ равносторонний пятиугольник, то восставим в точке В перпендикуляр ВС, равный линии АВ. Разделим линию АВ пополам в точке D опишем из точки D как из центра на расстоянии DC дугу СЕ, продолжим линию АВ до точки Е. Затем из каждой из точек А и В как из центров опишем на расстоянии АЕ дуги. Они пересекутся в точке G. Проведем линии AG и BG. Получим треугольник ABG - треугольник пятиугольника. В нем нуждаются при многих построениях. Затем из точек А и G как из центров на расстоянии  АВ опишем дуги; они пересекутся в точке Н. Затем так же из точек В и G  как из центров опишем дуги, пересекающиеся в точке F. Проведя линии AH, HG, GF,FB получим равносторонний и равноугольный пятиугольник ABFGH. Вот рисунок этого [рис. 36].

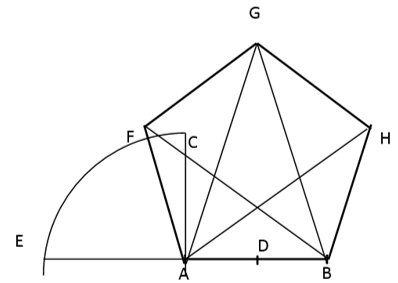
[рис 36].

[IV]. Если он сказал: как построить на линии АВ равносторонний пятиугольник, имея только раствор циркуля, равный линии АВ,так, чтобы его положение не изменялось, то восставим на линии АВ линию ВС, перпендикулярную к ней и равную линии АВ. Разделим линию АВ пополам в точке D как из центра на расстоянии АВ на линии DI пополам в точке К перпендикуляр КЕ, пересекающий линию АВ в точке Е.Далее из каждой из точек А и Е как из центров на расстоянии АВ опишем дуги, которые пересекутся в точке М. Проведем ВМ и продолжим ее в ее направлении до G и сделаем MG равной линии АВ. Соединим А иG. Примем  точки А и  G за центры и на расстоянии АВ отметим точку Н Примем точку B и G за центры и на расстоянии АВ отметим точку Н. Примем точки В и G за центры и на расстоянии АВ отметим  точку F. Проведем лини AH, HG, GF, FB. Получится равносторонний пятиугольник ABFGH. Вот рисунок этого [рис. 37].

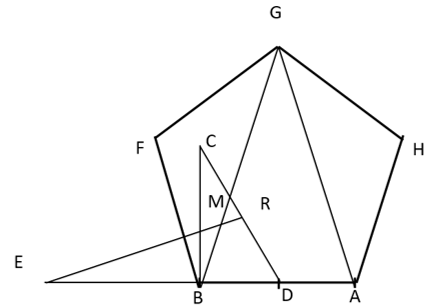
[рис 37].

[V] О построении шестиугольника. Если он сказал как построить равносторонний и равноугольный шестиугольник на линии АВ, то построим для этого равносторонний треугольник АВС. Продолжим линии АС и ВС в их направлении до точек Е и G. Построим на ВС еще один равносторонний треугольник ВСD. Продолжим линию DCв ее направлении до точки Н, сделаем линии СЕ, СG, CH равными линии СА и проведем линии DE, EG, GH, HA. Получится равносторонний и равноугольный шестиугольник ABDEGH. Вот рисунок этого [рис. 38].

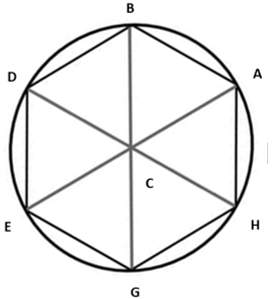
[рис 38].

[VI] О построении семиугольника. Если он сказал как построить на линии АВ равносторонний семиугольник, то сделаем линию ВС равной линии АВ, построим на линии АС равносторонний треугольник DAC и опишем около треугольник ADC круг, как показано в пятой главе. Проведем в нем хорду - линию АЕ, равную линии АВ, и разделим АЕ пополам в точке G, восставим перпендикуляр GH и продолжим его до окружности круга. разделим АВ пополам в точке F, восставим в ней перпендикуляр FI равный перпендикуляр GH. Проведем через точки А, В, и I круг АВI и отложим на нем дуги АК, KL, LI, IM, MN, NВ равные дуги АВ. Проведем линии АК, KL, LI, IM,MN,NB  это -равносторонний и равноугольный семиугольник. Вот рисунок этого [рис. 39].

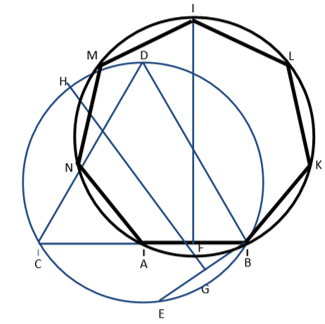
[рис 39].

[VII] О построении восмиугольника. Если он сказал как построить равносторонний восьмиугольник на линии  АВ, то продолжим АВ в ее направлении до точек С и D и постоим при каждой из точек А и В углы ЕАС и GBD, равные половине прямого. Сделаем каждую из линий АЕ и BG равной линии АВ , опустим из каждой точки Е и G перпендикуляры EC, GD  на линию DC и дополним квадрат CHKD.Сделаем каждую из линии HI, HF, KL, KM равной линии СЕ и соединим I и F, L и M. Получится равносторонний восьмиугольник ABGMLFIE. Вот рисунок этого [рис. 40].

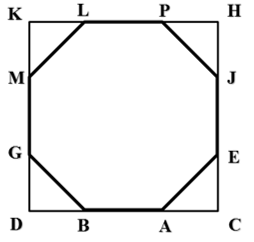
[рис 40].

[VIII] Если он сказал как построить равносторонний восьмиугольник на линии  АВ, имея только раствор циркуля, равный линии АВ, так чтобы его положение не изменялось , то постоим на линии АВ равносторонний и равноугольный четырехугольник ABCD, проведем линии СА и BD и продолжим их в их направлении до точек Е и G. Сделаем каждую из линии АЕ и В G равной лини АВ, соединим ЕG восставим к линии ЕG перпендикуляры равные линии  АВ, и соединим М и I . Продолжим каждую из линии ЕI и GM в их направлении до точек К и Н и разделим каждый из углов IMK и MIN пополам линиями ML и IF равной линии АВ и соединим FL. Получится равносторонний и равноугольный восьмиугольник Вот рисунок этого [рис. 41].

[рис 41].

[IX] О построении девятиугольника. Если он сказал как построить на линии АВ равносторонний и равноугольный девятиугольник, то опишем круг СDE произвольного размера с центром в точке G отметим на нем точку С примем ее за центра и на расстоянии полудиаметра круга отметим точки Е и D. Разделим дугу DE  на три равные части. Пусть одна такая дуга ЕН. проведем лини ЕG, EH, HG между линиями EG и HG линию FI равную линии АВ и параллельную линии ЕН. Примем точки А и В за центры и расстоянии FG опишем круги которые пересекутся в точке К. примем точку К за центр и на расстоянии КА опишем круг АВL. Разделим дугу ALB на восемь равных частей и соединим эти точки деление хордами. Получится равносторонний и равноугольный девятиугольник на линии АВ. Вот рисунок этого [рис. 42].

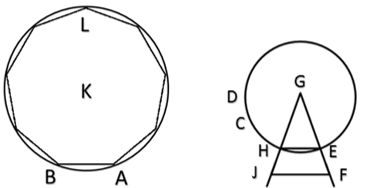
[рис 42].

[X] О построении десятиугольника. Если он сказал как построить на линии АВ десятиугольник, то разделим линию АВ пополам в точке С, восставим перпендикуляр BD в точке В, равный линии АВ, примем точку С за центр и на расстоянии CD отметим  Е на линии АВ. Далее из каждой из точек А и В как из центров на расстоянии АЕ опишем две дуги, пересекающиеся в точке G. Примем точку G за центр круга, в который [вписан] десятиугольник, сторона которого – линия АВ. Поэтому если мы опишем с центром G на расстоянии AG круг ABHF, продолжим линии  AG и  GB в их направлении  [до окружности круга ] до точек F и H, разделим каждую из друг АН и ВF на четыре равные части и соединим  точки деления хордами, тогда получим равносторонний и равноугольный десятиугольник. Вот рисунок этого [рис.43].

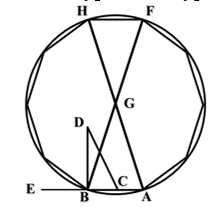
[рис 43].

 [ХI] Если он сказал: как построить на линии АВ десятиугольник с равными сторонамии углами, имея [только ]  раствор циркуля,13 об, [равный] линии АВ, то построим II на ней [треугольник] пятиугольника,как показано выше в четвертомпредложений. Пусть точка G -[вершина] угла, противолежащего линий АВ. Соединим линиями А и G.B и G. Примем точку G за центр и на расстоянии АВ опишем круг CDFH. Продолжим линий AG.BG в их направлении до  окружности круга [до точек F и С ]. Разделим каждую из друг НF и DC [ на четыре] равные [части,получим] части FI,IK, KM ,MN, CL, LN, NX, XD, проведем линии GF, GL, GL, GK, GM, [GL], GN, GX, GD [GC], GH и на каждой из этих линий, выходящих из центра, начиная от круга CDH,  линии, равные линии АD. Это – линий, на концах которых О. Соединим их прямыми линиями между собой и точами А и В. Получится равносторонний и равноугольный десятиугольный десятиугольник АВО³². Вот рисунок этого [рис 44].

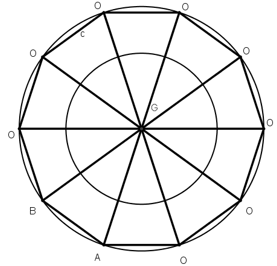
[рис 44].

Толығырақ

Центрдің бөліктері жайында5 

Бірінші  кітап

Шеңбер центрін анықтау туралы6

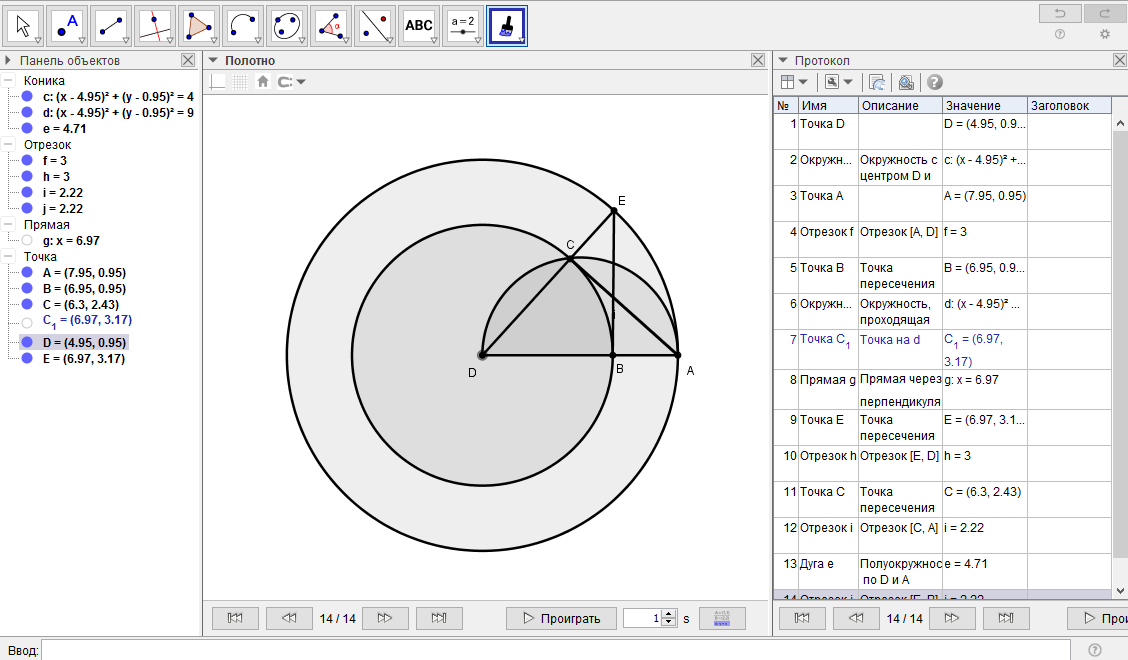
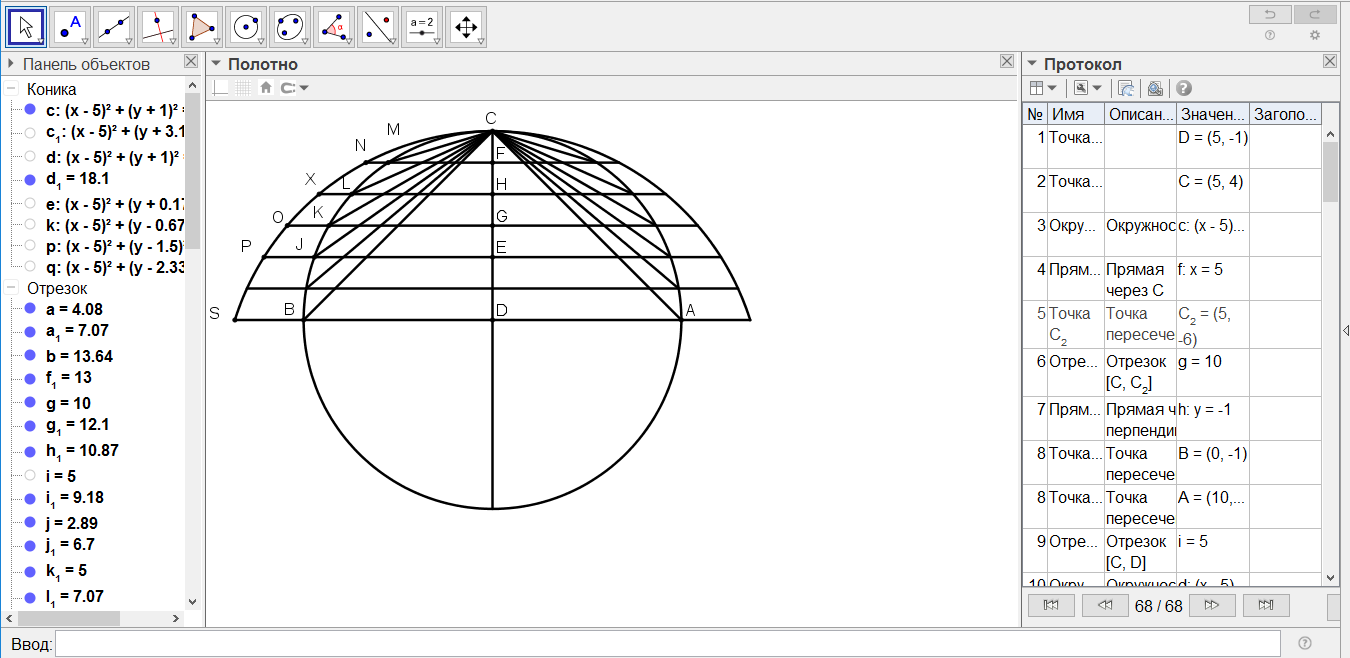
[I]   Егер ол сегментті толық шеңберге дейін қалай толықтыру керек десе, онда AВС сегментін саламыз да, В нүктесінде қақ бөлеміз. AВ және ВС сызықтарын жүргізіп, AВ мен ВС сызықтарындағы А және С нүктелерінің әрқайсысына ВСD және BAD  тік бұрышынтарын тұрғызамыз. ВD сызығын жүргізіп, оны Е нүктесінде қақ бөлеміз.Сонда E нүктесі ABC7 доғасының центрі болып табылады. Міне оның суреті:

 

1-сурет

 

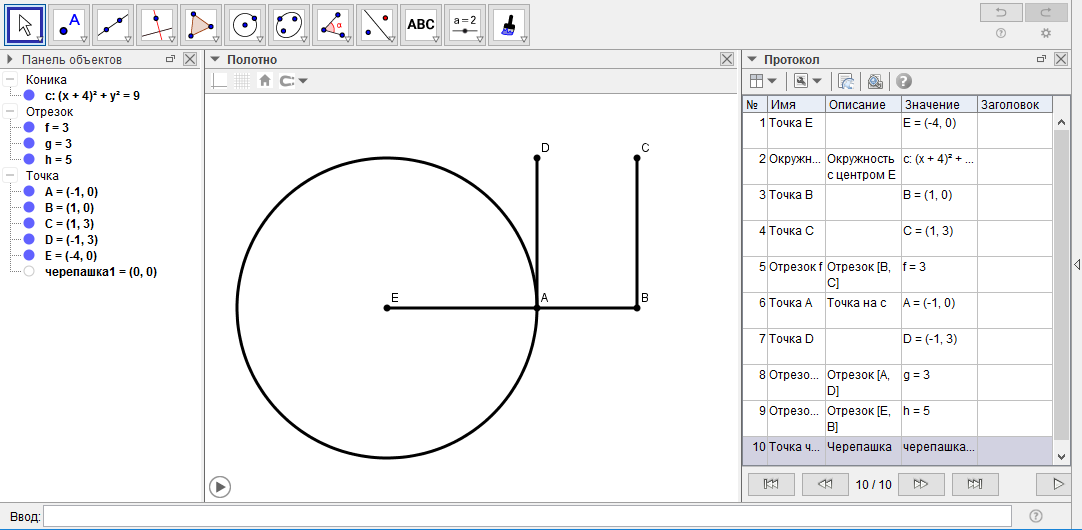
[II]   Егер ол центрі D нүктесі болатын ВС шеңберіне А нүктесінен қалай жанама жүргізуге болады десе, онда AD сызығын жүргіземіз. Ол ВС шеңберін В нүктесінде қияды. D центрінен DА қашықтықта AE шеңберін салайық. В нүктесінде АВЕ тік бұрышын тұрғызып, ВС шеңберін С нүктесінде қиятын ЕD сызығын жүргіземіз. А – мен С ны қосамыз. Сонда АС ВС шеңберіне жүргізілген жанама болып табылады. Міне оның суреті.

 

2-сурет

 

Математикалық негіздеу: Шеңберге жүргізілген жанама радиусқа перпендикуляр болады.

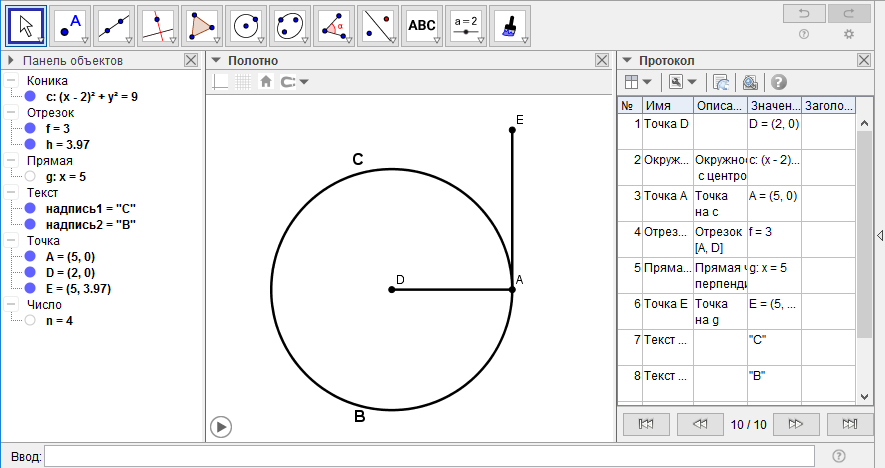
 [IIІ]   Егер ол жанаманы қолөнершінің тәсілі бойынша сал десе, онда сызғышты ВС сызығына орналастырып циркульді бір шамаға ашамыз; Егер оның бір ұшы сызғыш бойымен қозғалатын болса, онда екінші ұшы А нүктесі арқылы өтіп, ВС9-ға параллель сызықты береді. Міне оның суреті.

 

3-сурет

 

[IV]   Егер ол: А нүктесінен ABC дөңгелегінің шеңберіне жанаманы қалай жүргізеді десе, онда А нүктесін шеңбңрдің центрі D нүктесімен қосамыз, демек А мен D-ны [AD сызығымен] қосамыз. А нүктесінде AD сызығының бойымен DAE тікбұрышын тұрғызамыз. Сонда АЕ сызығы – ABC дөңгелегіне жанама болады10. Міне оның суреті.

 

4-сурет

 

[V]   Егер ол АВС үшбұрышының АВ және АС сызықтарының арасына ВС-ға параллель және берілген D [және егер ВС D сызығынан кіші болса] сызығына тең сызық сал десе, онда ВС сызығын оның бағытында [ВЕ D-ға тең болатындай Е нүктесіне дейін] созып, ал [егер ВС D сызығынан үлкен болса] D-ға тең ВЕ сызығын ВС сызығына саламыз. Е нүктесінен АВ сызығына параллель сызық жүргіземіз. Ол АС-ны G нүктесінде қиып өтеді. G нүктесінен ВС сызығына параллель сызық жүргіземіз; Бұл АВ-мен қиылысатын GH сызығы. Сонда GH D сызығана тең.  Міне оның суреті.

 

5-сурет

 

[VI] Егер ол АВС үшбұрышының АВ және АС сызықтарының арасына ВС сызығына параллель, мысалы АВ сызығында ол қиып алатын кесіндіге тең, яғни ЕВ сызығына тең DE сызығын салу керек болса, онда АСВ бұрышын BD сызығымен қақ бөлеміз де D нүктесінен ВС-ға параллель DE сызығын жүргіземіз. Сонда DE сызығы ЕВ сызығына тең. Міне оның суреті.

 

6-сурет

[VII] Егер ол АВС үшбұрышында мысалы, ВС сызығына параллель және ВЕ мен F сызықтарына тең DE сызығын сал десе, онда ВС сызығына  F сызығына тең BG сызығын салып, G нүктесі арқылы АВ-ға параллель GH сызығын жүргізіп, HGC бұрышын қақ бөлетін GD сызығын [G нүктесі арқылы] жүргіземіз де D нүктесінен ВС сызығына параллель DE сызығын жүргіземіз. Сонда DE сызығы  ВЕ және F сызықтарына тең. Міне оның суреті.

 

7-сурет

 

[VIII] басқа үшбұрышқа тең үшбұрышты салу туралы.  Егер ол қабырғалары басқа үшбұрыштың қабырғалырына тең үшбұрышты сал десе [мысалы АВС], онда DE түзу сызығын жүргіземіз де, АВ сызығына тең DG,  BC сызығына тең GH және СА тең HF сызығын  саламыз. G нүктесін центр ретінде қабылдап GD қашықтығында шеңбер бөлігін келтірейік, сол сияқты H нүктесін центр ретінде қабылдап HF қашықтығында шеңбер бөлігін келтіреміз. Бірінші бөлігі [екінші бөлігін] I нүктесінде қиып өтеді.ары қарай GI және ІH сызықтарын жүргізейік. Онда GIH үшбұрышының қабырғалары АВС үшбұрышының қабырғаларына тең. Міне оның суреті.

 

8-сурет

 

[IХ] Бұрышты тең үш бөлікке бөлу туралы. Егер ол АВС бұрышын тең үш бөлікке бөл десе, онда АВС бұрышы тік бұрышты болса, ВС сызығында тең қабырғалы DBC үшбұрышын тұрғызамыз. Сонда ABD бұрышы тік бұрыштың үштен бір бөлігі. DBC бұрышын қақ бөлеміз15.  Міне оның суреті.

 

9-сурет

 

[Х] Егер бұрыш тік бұрыштан кіші болса, онда В нүктесін центр ретінде қабылдап ВА қашықтықта DAС шеңберін келтіреміз.BD ны ВС-ға тік бұрыш бойынша қойып, СВ-ны шеңбермен қиылысқанша Е нүктесіне созамыз. Сызғышты А нүктесіне акеліп оны CDE дөңгелегінің шеңбері бойынша DB перпендикуляры және DE доғасының арасында жатқан HF сызығы DB сызығына тең болғанша қозғайтын боламыз, бұл жағдайжа сызғыш А нүктесінен таймайды. Ары қарай EF доғасына тең EK доғасын саламыз да KB жүргіп L нүктесіне дейінгі бағытта жалғаймыз. Онда LBC бұрышы АВС бұрышының үштен бірі болады. Әрі қарай ABL бұрышын қақ бөлеміз. Міне оның суреті. 

 

10-сурет

 

[ХІ] бұрышты тең үшке бөлудің басқа тәсілі.  АВС сүйір бұрышын тұрғызайық та және егер біз оны тең үш бөлікке бөлгіміз келсе А нүктесінен AH перпендикулярын [ВС сызығына нүктеден түсіреміз]. В нүктесіне сызғышты әкеліп, AD мен AH сызықтарының арасына орналасқан сызық екі еселенген АВ болғанша қозғайтын боламыз. Бұл мысалы DEB сызығы, демек DE сызығы екі еселенген АВ сызығы болып табылады. Ендеше DBC бұрышы АВС бұрышының үштен бір бөлігі. Міне оның суреті.

 

11-сурет

 

[ХІІ] Доғаны тең үш бөлікке бөлу туралы. Егер ол ABD доғасын тең үш бөлікке бөлу керек десе, онда осы доға орналасқан шеңбердің центрін табамыз. Бұл Е нүктесі болсын. А мен Е-ні, Е мен D-ны қосып, ABCD доғасын В мен С нүктелерінде қиып өтетін ЕВ және ЕС сызықтарымен AED бұрышын үш тең бөлікке бөлеміз. Сонда ABCD доғасы үш тең бөлікке АВ, ВС және СD доғаларына бөлінетін болады. Міне оның суреті.

 

12-сурет

 

[ХІІІ] Екі еселенген басқа үйге немесе шарға тең немесе басқа қатынаста алынған үй немесе шар салу туралы. Егер ол ұзындығы, ені, биіктігі өзара тең екі еселенген басқа үй болып табылатын квадрат үйді салу керек болса немесе басқа екі еселенген болып келген шарды салу, немесе қақ бөліп немесе басқа бір қатынастарда болып табылатын шарды қалай салу керек десе, онда үй ұзындығына және шар диаметріне тең АВ сызығын тұрғызамыз, екі еселенген  тік бұрыш бойынша АВ сызығына АС сызығынсалып, DABC жазық фигурасын ьстолықтырамыз. AD мен ВС диагоналдарын жүргіземіз. Олар F нүктесінде қақ бөлінеді. Олардың бағытында DC мен DB сызықтарын созамыз. Шызғыштың шетін А нүктесіне қоямыз да оны GC және EB  сызықтары бойынша [ол оларды Е және G нүктелерінді қиылысқанша] GF пен FE тең болатындай болғанша қозғаймызтын боламыз.  Сонда үйдің ұзындығы немесе шардың диаметрі ВЕ19 сызығы болады.  Міне оның суреті.

 

13-сурет

 

[ХІV] Өртегіш айна жасау туралы. Егер біз күн сәулелерінің көмегімен бір қашықтықтан затты өртейтін айнаны жасағымыз келсе, онда алдымен айнаны айқындайтын (лекало) даяр үлгісін жасайық. Ол үшін  шеңбер салайық, оның жарты диаметрі өртегіміз келетін заттың ара қашықтығының шамасына тең. Бұл АВС шеңбері болсын. Оның ADC диаметрін жүргізейік. DC сызығына С  нүктесінен бірнеше тең кесінділер салайық. Бұл кесінділер кіші болған сайын даяр үлгі жақсырек және дәл болады. Бұл кесінділер CF, FH, HG, GE және ED болсын. D нүктесі арқылы [CD-ға] тік бұрыш бойынша E,G,H және F сызықтарын жүргізейік те оларды екі жағына да B, I, K, L және М нүктелеріне дейін созайық. C мен В, С мен I, С мен K, С мен L, С мен М нүктелерін қосайық. CM сызығына тең FN сызығын, CL-ге тең HX, CK-ға тең GO CI-ге тең EP және СВ-ға тең DS сызығын салайық. C, N, X, O, P және S нүктелерін қосайық та осы сызық бойынша лекало жасайық. Сосын металдан мысалы темірден, қоладан, мыстан немесе цинктен айна дайындайық та,  егер мүмкін болса оны ысып жалтыратайық. Егер айна қисық болып шықса, оны даяр үлгісі бойынша даяр үлгіні айнаға С нүктесі даяр үлгінің ортасына дәл келетіндей айнаның даяр үлгімен беттесуіне қол жеткізетіндей етіп лекалды айнаға беттестіріп түзетеміз. Сонда үлкен өртегіш күші20 бар өртегіш айнаны аламыз. Міне оның суреті.

 

14-сурет

 

[ХV] Өртегіш айна жасаудың екінші тәсілі.  Егер оны біз жасағымыз келсе, онда кез келген қашықтықты, оның жартысы АВ сызығы болсын, аламыз да, оны С нүтесіне дейінгі оның бағытына созамыз. В нүктесіне ВС-ға перпендикуляр DB сызығын қарама-қарсы екі жағына да орнатайық та, ВС сызығына өзара тең кіші сызықтарды BE, EG, GH және HC салайық. F нүктесінде АЕ-ні қақ бөліп, F центрінен FA  қашықтықта шеңбер сызайық. Ол BD сызығын I нүктелерінде қияды. I нүктелерінен AC сызықтарына параллель IL сызықтарын жүргізейік те  Е нүктесінен BD сызығына параллель сызықты L нүктелеріне дейін жүргізейік. Сосын AG сызығын М нүктесінде қақ бөліп М нүктесінен  МА қашықтықта шеңбер сызамыз. Ол BD сызығын N нүктелерінде қияды. N нүктелерінен АС сызығына параллель NX сызықтарын Х нүктесіне дейін жүргіземіз. Сосын АН сызығын О нүктесінде қақ бөліп, О центрінен ОА қашықтықта шеңбер сызамыз. Ол BD сызығын Р нүктелерінде қияды. Р нүктелерінен ВС –ға параллель Z нүктелеріне дейін сызықтар жүргізейік. B, L, X және Z нүктелерін сызықпен қосып, дая үлгі аламыз. Егер біз даяр үлгіні тексеретін болсақ оны В нүктесіне айнаның ортасына орналастырамыз. Сонымен біз үлкен өртегіш күші бар өртегіш айна аламыз.  Міне оның суреті.

 

15-сурет

1.2  Есеп. Сегментті толық шеңберге толтыру керек болса, онда: 

Салудың алгоритмі:

1. AВС сегментін саламыз да В нүктесінде тең екіге бөлеміз.
2. AВ және ВС нүктелерін қосамыз.
3. А және С нүктелерінен ВСD және BAD тік бұрышын тұрғызамыз,
4. E нүктесі ABC шеңберінің центрі болып табылады.

1-сурет

Сонда АС кесіндісі ВС дөңгелегіне жүргізілген жанама болады.

Математикалық негіздеу: Тікбұрышты үшбұрышқа сырттай сызылған шеңбердің центрі гипотенузаның  қақ ортасында жатады.

1.2   Дөңгелекке жанама жүргізу жолдары.

Есеп. Центрі D нүктесі болатын ВС дөңгелегіне А нүктесінен жанама жүргізу.

Салудың алгоритмі:

1. Центрі D нүктесі болатын ВС дөңгелегіне А нүктесінен жанама жүргізу үшін AD кесіндісін жүргіземіз.
2. AD кесіндісі ВС дөңгелегін В нүктесінде қияды. D центрі арқылы радиусы AD болатындай AE дөңгелегін сызамыз.
3. В нүктесі арқылы АВЕ тік бұрышын тұрғызып, ВС дөңгелегін С нүктесі арқылы кесетін ЕD кесіндісін жүргіземіз.
4. А және С нүктелерін қосамыз.

Сонда АС кесіндісі ВС дөңгелегіне жүргізілген жанама болады.

Математикалық негіздеу: Шеңберге жүргізілген жанама радиусқа перпендикуляр болады.

1.3 Есеп. Центрі Е нүктесі болатын дөңгелекке жанама жүргізу.

Салудың алгоритмі:

3-сурет

Қолөнерші (ремесленник) әдісімен салсақ

1. Е нүктесінен шеңберді А нүктесінде қиятын ВС кесіндісіне перпендикульяр ЕВ кесіндісін сызамыз.

2. Циркульді АВ кесіндісіне тең болатындай ашып бір басын ВС кесіндісіне қоямыз

3. Бір басы ВС кесіндісінің бойымен жылжитындай циркульдің екі басын бірдей жылжытамыз.

Сонда АD кесіндісі дөңгелекке жүргізілген жанама болады.

Математикалық негіздеу: ЕВС=90, AD кесіндісі АВ парраллель болғандықтан ЕАD=90.  Шеңберге жүргізілген жанама радиусқа перпендикуляр болады

1.4 Есеп. АВС дөңгелегінің бойында жатқан А нүктесі арқылы жанама жүргізу.

Салудың алгоритмі:

1. А нүктесімен дөңгелектің D центрін қосамыз.

2. А нүктесінен өтетін DAE тік бұрышын тұрғызамыз.

4-сурет

Сонда АD кесіндісі дөңгелекке жүргізілген жанама болады.

Математикалық негіздеу: Шеңберге жүргізілген жанама радиусқа перпендикуляр болады

1.5 Есеп. АВС үшбұрышында АВ және АС қабырғаларында жататын, ВС табанына параллель, D кесіндісіне тең кесінді жүргізу керек болса, онда

Салудың алгоритмі:

1. Егер ВС<D болса онда, ВС қабырғасын ВЕ=D болатындай Е нүктесіне дейін созамыз.
2. Егер ВС>D болса онда, ВС қабырғасын ВЕ=D болатындай Е нүктесін белгілейміз.
3. Е нүктесінен АВ қабырғасына параллель болатын ЕH кесіндісін саламыз.
4. G нүктесінен CВ қабырғасына параллель болатын GH кесіндісін саламыз.
5. Сонда GH=D болады.

5-сурет

Сонда HG BC қабырғасына параллель және HG=D кесіндісіне тең болады.

Математикалық негіздеу:

 1.6 Есеп. АВС үшбұрышында төбесі АВ және АС қабырғаларында жататын,  ВС табанына параллель, мысалы EB тең болатындай DЕ кесіндісін салу керек болса, онда

Салудың алгоритмі:

1. АВС бұрышын тең екіге бөлетіндей DE түзуін жүргіземіз.
2. АС қабырғасында жататын D нүктесі арқылы ВС-ға параллель DЕ кесіндісін жүргіземіз.
3. Сонда DE=EB болады.

6-сурет

Сонда DЕ ВС қабырғасына параллель және ЕВ және Fкесіндісіне тең болады.

Математикалық негіздеу: CBD= ABD және СВ DE болғандықтын, CBD= BDE, демек BDЕ= DВЕ, яғни BDE үшбұрышы тең бүйірлі болғандықтын DE=EB болады.

1.7 Есеп. АВС үшбұрышында ВС қабырғасына параллель ВЕ және F кесінділеріне тең болатындай DE кесіндісін жүргізу керек.

Салудың алгоритмі:

1. ВС қабырғасынын F кесіндісіне тең болатындай ВG кесіндісін белгілейміз.
2. G нүктесінен АВ қабырғасына параллель болатын GH кесіндісін саламыз.
3. HGC бұрышын қақ бөлетіндей GD кесіндісінін саламыз.
4. D нүктесінен ВС қабырғасына параллель болатындай DЕ кесіндісін сызамыз.

             7-сурет

Сонда DЕ ВС қабырғасына параллель және ЕВ және Fкесіндісіне тең болады.

Математикалық негіздеу:

1.8 Есеп. Бір үшбұрышқа тең екінші үшбұрышты салу керек болса, онда

Салудың алгоритмі:

1. DE түзуін сызып, оның бойынан DG=АВ, GH=BC, HF=CA болатындай DG,GH,HF кесінділерін белгілейміз.
2. Центрі G болатындай r=GD жартышеңберін саламыз.
3. Центрі H болатындайr=HF жартышеңберін саламыз. Екі жартышеңбер I нүктесінде қилысады.
4. GI және IHтүзулерін жүргіземіз.

                             8-сурет

Сонда GIH үшбұрышы ABC үшбұрышына тең болады.

Математикалық негіздеу: Үшбұрыштар теңдігінің бірінші белгісі.

 1.9 Есеп. Егер АВС тікбұрышын тең үшке бөлу керек болса, онда

Салудың алгоритмі:

1. DС түзуіне тең қабырғалы DBC үшбұрышын тұрғызамыз.Сонда ABD бұрышы ABC бұрышының үштен біріне тең болады.
2. DBC бұрышын қақ бөлеміз.

                                                                                   9-сурет

Сонда ABC бұрышы тең үшке бөлінеді.

Математикалық негіздеу: 90-60=30, 60:2=30

 1.10  Есеп. Егер АВС сүйір бұрышын тең үшке бөлу керек болса, онда

Салудың алгоритмі:

1. В нүктесін центр етіп алып ВА қашықтықпен DAC шеңберін сызамыз.
2. Сызғышты А нүктесіне қойып, BC ВD жүргіземіз.
3. ВС түзуін шеңбермен Е нүктесінде қилысқанға дейін созамыз.
4. Сызғыштың бір басын А нүктесіне қойып, екінші басын CDE шеңбері бойымен DB және DE перпендикульярларының арасында жататын HF =DB болғанға дейін жылжытамыз.
5. EF доғасына тең EK доғасын тұрғызамыз.
6. KB түзуін L нүктесіне дейін созамыз.

                   10-сурет

Сонда LBC бұрышы ABC бұрышының үштен біріне тең болады.

Математикалық негіздеу:

1.11 Есеп. Бұрышты тең үшке бөлудің басқа әдісі

Салудың алгоритмі: АВС сүйір бұрышын теңдей үшке бөлу керек болса, онда

1. А нүктесінен AH ВC болатындай АН жүргіземіз.
2. ВС параллель болатындай AD түзуін жүргіземіз.
3. Сызғыштың бір басын В нүктесіне қойып, екінші басын ВD=2*AB болатындай BD түзуін жүргіземіз.

Сонда DBC бұрышы ABC бұрышының үштен біріне тең болады.

Математикалық негіздеу:

1.12 Есеп. Доғаны тең үшке бөлу керек болса, онда

Доға орналасқан шеңбердің центрін тауып оны Е деп белгілейміз.Салудың алгоритмі: АВС доғасын теңдей үшке бөлу керек болса, онда

1. AE және ED нүктелерін қосамыз.
2. AED бұрышын теңдей үшке бөлеміз де, доғамен қилысу нүктелерін В және С деп белгілейміз.

Сонда ABC[D] доғасы AB, BC және CD болып тең үшке бөлінеді.

Математикалық негіздеу: AED бұрышын теңдей үшке бөлгендіктен доға да тең үшке бөлінеді.

1.13 Есеп. Берілген үйден немесе шардан екі есе, болмаса бірнеше есе үлкен көлемде үй немесе шар салу керек болса, онда

Салудың алгоритмі: Берілген үйден екі есе, болмаса бірнеше есе үлкен биіктігі, ені және ұзындығы бірдей шаршы түрде үй немесе берілген шардан еселенген шарды немесе қақ бөлінген, болмаса басқа өлшемдегі шар салу керек болса, онда

1. Шардың диаметріне немесе үйдің ұзындығына тең АВ кесіндісін саламыз.
2. AВ-дан екі есе ұзын болатындай АС кесіндісін АВ-ға тік бұрышпен салып, пайда болған фигураны DABC фйгурасына толықтырамыз.
3. AD және ВС диагональдарын жүргіземіз, олар F нүктесінде қилысады.
4. DC және DB сызықтарын өз бағыттарымен созамыз.
5. Сызғыштың қырын А төбесіне қоямыз да, GC және EB сызықтарының бойымен GF=FE (E және G нүктелерінде қияды деп есептейміз) болғанға дейін жылжытамыз.

Сонда үйдің ұзындығы немесе шардың диаметрі ЕВ болып табылады.

Математикалық негіздеу: ????????????????

1.14  Есеп. Жандырғыш айна салу керек болса, онда

Салудың алгоритмі: Егер күн сәулесі арқылы алыстағы затты жандыратын айна салу керек болса, онда алдымен айнаның қалыбын (лекало) жасап алу керек. Ол үшін

1. Жарты диаметрі біз жағатын заттың қашықтығына тең болатындай шеңбер тұрғызамыз. Бұл шеңберді АВС деп алайық.
2. AСD диаметрін жүргіземіз.
3. DC түзуінің бойынан С нүктесінен бірдей бірнеше кесінділер сызамыз.
4. Бұл кесінділер неғұрлым қысқа болған сайын қалыбымыз (лекало) соғұрлұм дәл болады. Бұл кесінділерді CF, FH, HG, GE, ED деп алайық.
5. D нүктесі арқылы өтетін, CD түзуіне перпендикульяр E,G,H,F түзулерін екі бағытқа қарай B,I,K,L,M нүктелеріне дейін созамыз.
6. C және B, C және I, C және K, C және L, C және M нүктелерін қосамыз.
7. CM-ге тең FN, CL-ге тең HX, CK-ге тең GO, CI-ге тең EP, CB-ге тең DS түзулерін жүргіземіз.
8. C,N,X,O,P және S нүктелерін қосып, осы сызықтар негізінде қалыпты жасаймыз.
9. Содан соң айнаны металлдан жасаймыз. Мысалы темірден, болаттан, мыстан немесе цинктан жасаймыз, мүмкін болса барынша жалтыратамыз.
10. Егер айна қисық болса, онда С нүктесін қалыптың ортасына келетіндей етіп айнаны түзетеміз.

Сонда үлкен күші бар жандырғыш айна жасалады.

Математикалық негіздеу: ????????????????

1.14 Есеп. Жандырғыш айна салудың екінші жолы.

Салудың алгоритмі: Егер күн сәулесі арқылы алыстағы затты жандыратын айна салу керек болса, онда

1. Жартысы АВ –ға тең болатындай кез-келген қашықтықтағы Жарты диаметрі біз жағатын заттың қашықтығына тең болатындай шеңбер тұрғызамыз. Бұл шеңберді АВС деп алайық.
2. AСD диаметрін жүргіземіз.
3. DC түзуінің бойынан С нүктесінен бірдей бірнеше кесінділер сызамыз.
4. Бұл кесінділер неғұрлым қысқа болған сайын қалыбымыз (лекало) соғұрлұм дәл болады. Бұл кесінділерді CF, FH, HG, GE, ED деп алайық.
5. D нүктесі арқылы өтетін, CD түзуіне перпендикульяр E,G,H,F түзулерін екі бағытқа қарай B,I,K,L,M нүктелеріне дейін созамыз.
6. C және B, C және I, C және K, C және L, C және M нүктелерін қосамыз.
7. CM-ге тең FN, CL-ге тең HX, CK-ге тең GO, CI-ге тең EP, CB-ге тең DS түзулерін жүргіземіз.
8. C,N,X,O,P және S нүктелерін қосып, осы сызықтар негізінде қалыпты жасаймыз.
9. Содан соң айнаны металлдан жасаймыз. Мысалы темірден, болаттан, мыстан немесе цинктан жасаймыз, мүмкін болса барынша жалтыратамыз.
10. Егер айна қисық болса, онда С нүктесін қалыптың ортасына келетіндей етіп айнаны түзетеміз.

Сонда үлкен күші бар жандырғыш айна жасалады.

Математикалық негіздеу: ????????????????

asd

Целью проекта является показать пути эффективного использования математических наследий аль-Фараби в современном математическом образовании с помощью новых информационных технологий, согласовывая их содержание с сегодняшним содержанием математики.

В результате проведения данного исследования реализуется обучение математике с одной стороны, т.е. обучение математическим наследиям аль-Фарби; обучение информатике, с другой стороны, т.е. обучение математическим наследиям аль-Фараби разработав электронные средства обучения.

Для достижения поставленной цели были определены следующие задачи:

- исследуя геометрию, тригонометрию, арифметику, алгебру и теорию музыки аль-Фараби, математически обосновать их с точки зрения современной эпохи;

- разработать учебно-методическое пособие, электронные средства обучения с помощью информационных и коммуникационных технологий, предназначенные для обучения геометрическим построениям по алгоритмам, предлагаемых аль-Фараби и тригонометрии, арифметике, алгебре и теории музыки аль-Фараби;

- предложить эффективную методику обучения алгоритмам построения правильных многоугольников аль-Фараби и тригонометрии, арифметике, алгебре и теории музыки аль-Фараби с помощью электронных средств обучения и их использования в учебном процессе;  

- проектирование рассмотрения, реализация и дальнейшее развитие результатов проведенных исследований, разработанных электронных средств обучения в рамках образовательного портала.

В результате своевременного выполнения выше указанных задач ожидается разработка:

- математического обоснования геометрии, тригонометрии, арифметики, алгебры и теории музыки аль-Фараби, с точки зрения современной эпохи;

- электронных средств обучения с помощью информационных и коммуникационных технологий, предназначенных для обучения геометрическим построениям по алгоритмам, предлагаемых аль-Фараби и тригонометрии, арифметике, алгебре и теории музыки аль-Фараби;

- эффективной методики обучения алгоритмам построения правильных многоугольников аль-Фараби и тригонометрии, арифметике, алгебре и теории музыки аль-Фараби с помощью электронных средств и их использования в учебном процессе; 

- образовательного портала, организованного в целях представления результатов проведенных исследований, разработанных электронных средств, для массового рассмотрения.