Үшбұрыштарды бөлу туралы

[I] Егер ол ABC үшбұрышын сызықпен қалай қақ бөлеміз десе, онда оның бір бұрышынан сызық жүргіземіз; біз сызық жүргізетін бұрышымыз А  бұрышы болсын. ВС сызығын D нүктесінде қақ бөлеміз де A және D сызықтарын қосамыз. AD сызығымен қақ бөлінген ABC үшбұрышын аламыз.

Міне оның суреті [73 – сурет].

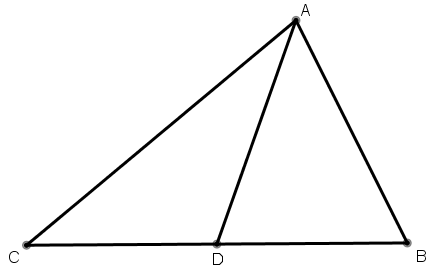
[73 – сурет].

 

[IІ] Егер ол ABC үшбұрышын сызықпен қалай қақ бөлеміз десе, онда [А] нүктесінен қарсы жатқан қабырғаға перпендикульяр түсіреміз; бұл  D нүктесі. Егер біз осыны алғымыз келсе, онда  BC сызығын қақ бөлеміз. Егер бөлінді D нүктесімен сәйкес келсе онда AD сызығын жүргіземіз де AD сызығымен қақ бөлінген ABC үшбұрышын аламыз. Егер BC сызығы D нүктесінде қақ бөлінбесе, BC сызығының ортасы E нүктесі болсын деп есептейік. Онда егер A мен E–ні, A мен D–ны қосып, E нүктесінен  AD сызығына параллель EG сызығын жүргіземіз де, D мен G–ні қосамыз сонда ABC үшбұрышы DG сызығымен қақ бөлінеді. Міне оның суреті [74 – сурет].

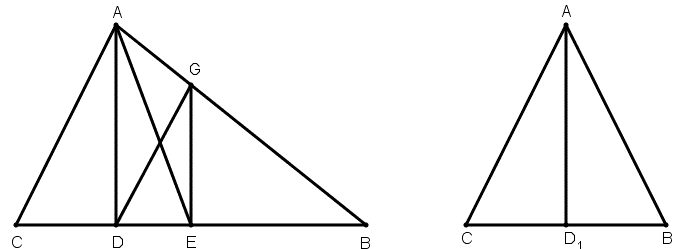
[74 – сурет].

 

[IIІ] Егер ол ABC үшбұрышын сызықтармен теңдей төрт бөлікке қалай бөлеміз десе, онда B нүктесінен бастап BC сызығын теңдей төрт бөлікке бөлеміз. BC сызығына AD перпендикулярын тұрғызамыз. Бөлінген орыннан AD сызығына параллель болатындай EL, GK, HF сызықтарын жүргіземіз және D мен L–ді, D мен K–ны, D мен F–ті сызықтармен қосамыз. Сонда BDL, DLK, DKF және DFC–ға теңдей төртке бөлінген ABC үшбұрышын аламыз. Міне оның суреті [75 – сурет].

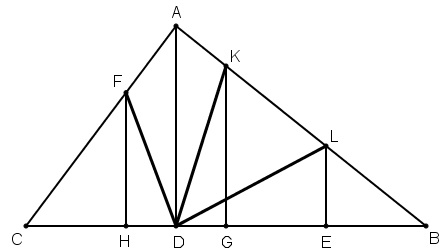
[75 – сурет].

 

Дәл осындай жолмен үшбұрышты теңдей үш бөлікке, бес бөлікке немесе басқа да теңдей бөліктерге бөлуге болады.

[IV] Егер ол ABC үшбұрышын ABC үшбұрышының бір қабырғасына параллель сызықпен қалай қақ бөлуге болады десе, бұл BC қабырғасы болсын делік,  онда AC–ның жартысына тең AC сызығының бағытында белгілейміз AD. DC сызығына жарты дөңгелек тұрғызамыз да, DC–ға AE перпендикулярын тұрғызамыз, AE–ге тең болатындай AG сызамыз да, BC сызығына параллель GH сызығын жүргіземіз, сонда GH сызығымен қақ бөлінген ABC үшбұрышын аламыз.

Міне оның суреті [76 – сурет].

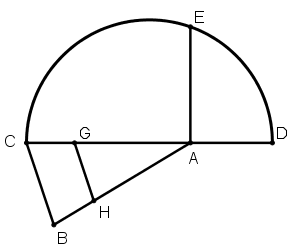
[76 – сурет].

 

[V]  Егер ол ABC үшбұрышын ВС сызығына параллель екі сызықпен қалай теңдей үшке бөлу керек десе, онда АС сызығының бағытында АС–ның  үштен біріне тең  AD сызығын белгілеп, АС–ның үштен екісіне тең АЕ сызығын салып, DC және СЕ сызықтарынының әрқайсысына  жарты дөңгелектер жүргіземіз де, АС сызығына AGH перпендикуляр тұрғызып, AG сызығына тең  AF сызығын  және АН сызығына тең болатын AJ сызығын белгілейміз.  ВС сызығына параллель  ІК және FL сызықтарын жүргіземіз, сонда тең үш бөлікке бөлінген ABC үшбұрышын аламыз: Бұл– ALF, FLKJ және ВКJС. Міне оның суреті [77 – сурет].

 

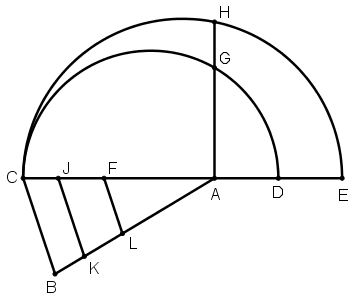
[77 – сурет].

 

Егер біз үшбұрышты төрт немесе одан да көп тең бөліктерге бөлгіміз келсе, тағы да осы салуларды пайдаланамыз.

 

  [VI] Үшбұрышты теңдей үш бөлікке бөлудің екінші тәсілі.  Егер қаласаңыз, АС сызығының үштен екісіне тең AD сызығын жүргіземіз, DC сызығына жарты дөңгелек саламыз, АЕ сызығына  перпендикуляр саламыз, АЕ  перпендикулярына тең AG сызығын аламыз және  ВС сызығына параллель GH сызығын жүргіземіз. Бұдан кейін осы тараудың басында сипатталғандай AGH үшбұрышын тең екіге  бөлеміз,  теңдей үш бөлікке бөлінген ABC үшбұрышын аламыз: AFI, FHGL, HBCG. Міне оның суреті [78 – сурет].

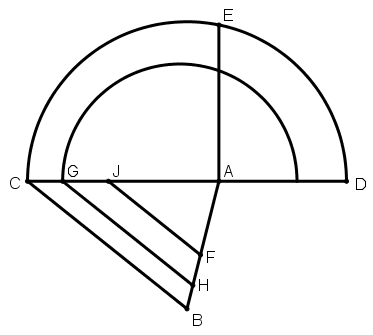
[78 – сурет].

 

   [VII] Үшбұрыш туралы басқа есеп. Егер ол ABC үшбұрышын оған тең ауданға ВС сызығына параллель сызық арқылы қалай үлкейтуге болады десе, онда АС сызығына екі еселенген AD сызығын саламыз.  CD сызығына  DEC жарты дөңгелегін сырттай жүргіземіз де,  АС сызығына  АЕ перпендикулярын түсіреміз, АЕ сызығына тең АН сызығын жүргіземіз, H нүктесінен ВС сызығына параллель HG сызығын жүргіземіз, AB сызығын [HG] сызығымен қиылысқанша созамыз. Сонда  CG фигурасы ABC үшбұрышына  тең  болады. Міне оның суреті [79 – сурет]. Егер үшбұрышты үш, [төрт] немесе оданда көп есеге⁴⁹ үлкейткіміз келсе, дәл осылай жасаймыз.

 

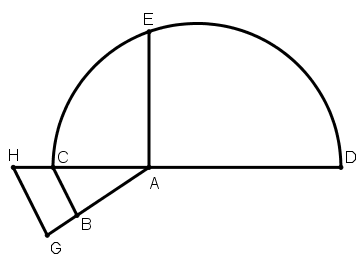
[79 – сурет].

 

[VIII]  Егер ол ABC үшбұрышына А нүктесі арқылы өтетін сызықпен, осы үшбұрышқа тең немесе одан екі, үш және бірнеше есе үлкен фигураны қалай қосуға болады десе, онда ВС сызығын  екі немесе үш есеге үлкейтеміз; сөйтіп   BD сызығын аламыз да, А мен D–ны қосамыз. Сонда  АВD  үшбұрышы ABС үшбұрышына тең немесе одан екі есе үлкен болады. Міне оның суреті [80 – сурет].

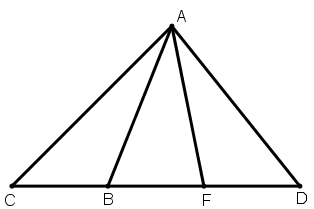
[80 – сурет].

 

[IX]  Егер ол ABC үшбұрышының ортасына оған ұқсас және оның жартысына немесе үштен біріне, немесе басқа бөлігіне тең үшбұрышты қалай салу керек десе, онда оның ортасынан D нүктесін белгілеп, A мен D–ны, B мен D–ны және D мен C–ны қосамыз да АЕ сызығы AD–ның жартысына немесе үштен бір бөлігіне, немесе төрттен бір бөлігіне тең болатындай етіп AD бағыты бойынша Е нүктесіне дейін созамыз. ED–нің бойына жарты дөңгелек саламыз да, AG перпендикулярын тұрғызамыз, DH–ты AG–ге тең етіп саламыз. Басқа сызықтармен де осы салуды орындаймыз. Сонда Н, F және J нүктелері пайда болады. Осыларды қосып, ABC үшбұрышының ішінен өзіміздің салғымыз келген–HFJ үшбұрышы аламыз. Міне оның суреті [81 – сурет].

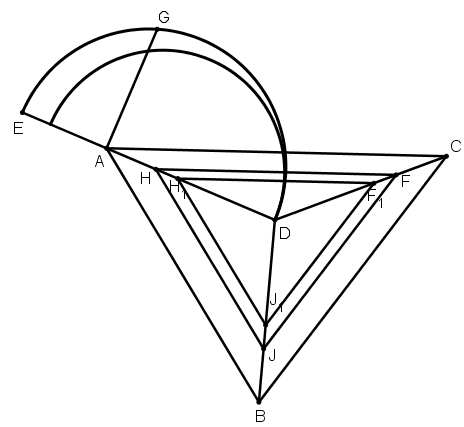
[81 – сурет].