Дөңгелекке іштей сызылған фигураларды салу туралы

Қолөнершілер дөңгелекке іштей сызылған және сырттай сызылған фигураларды дөңгелекті қалауынша [тең] бөліктерге бөлу арқылы тұрғызатындығын біліп қой.  Мысалы дөңгелекке іштей сызылған бесбұрышты салу үшін оны тең бес бөлікке бөліп, бөлу орындарын қосады және бөлу орындарынан дөңгелекті жанап өтетін сызықтар жүргізеді де, сонымен тең қабырғалы, тең бұрышты іштей сызылған бесбұрыш және сырттай сызылған [сондай бесбұрыш] тұрғызады. Бұл салу алтыбұрыш үшін тіпті ысылмаған қолөнерші үшін де күрделі емес. Жақсы өнер жасау үшін қолөнерші осы тарауды біздің дәлелдегендерімізге сәйкес бесбұрыш, алтыбұрыш, онбұрыш, тағы басқа фигуралардың қабырғаларына [тең қашықтықта] қосылған бірнеше таңбаларды айналдыра ұрғылап [салады]. Циркульді көп рет ашып жауып қозғалта бөлуді іске асыратындар тілегіне тек үлкен еңбекпен жуықтап қана жетеді. Егер сіз біз көрсеткендей бұл фигуралардың қабырғаларын анықтауда белгілі өнер жолына кіріссеңіз онда білгін, егер сен осы фигуралардың біреуінің дөңгелекке іштей сызылғанын салсаң және осы фигураны салуың дұрыс болса, онда егер сен бөлу орындарынан дөңгелекті жанап өтетін сызықтар жүргізсең сызбада оны сырттай салған фигура шығады³³.  Фигураларға сырттай сызылған және оларға іштей сызылған дөңгелектер жайында айтсақ, онда олар алуан түрлі, ал бұл кітапта  олардың әрқайсысы туралы оларды қалай салу керектігі дәлелденген³³.

[І] Дөңгелекке іштей салынған үшбұрышты салу. Егер біз дөңгелекке іштей сызылған теңқабырғалы үшбұрышты салғымыз келсе, онда центрі D нүктесінде болатын АВС дөңгелегін салып, оның ішіне ADE диаметрін жүргіземіз, Е нүктесін центр етіп қабылдаймыз да ED қашықтықта В мен С нүктелерін белгілеп, АВ, АС және ВС сызықтарын жүргіземіз. Сонда теңқабырғалы АВС үшбұрышын аламыз³⁴. Міне оның суреті [28 сурет].

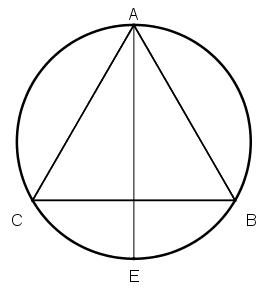
[28 сурет].

[ІІ] Шеңберге сырттай сызылған үшбұрышты салу. Егер біз дөңгелекке сырттай сызылған теңқабырғалы үшбұрышты салғымыз келсе, онда оның ішіне теңқабырғалы АВС үшбұрышын сызамыз да, А, В және С нүктелерінің әрқайсысынан G, H және F нүктелерінде кездескенге дейін жанама сызықтар жүргіземіз. Сонда теңқабырғалы HGF³⁵ үшбұрышын аламыз. Міне оның суреті [29 сурет].

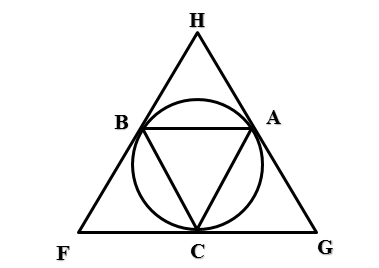
[29 сурет].

 

[ІІІ] Шеңберге іштей сызылған шаршыны салу. Егер ол дөңгелекке іштей сызылған теңқабырғалы және тең бұрышты төртбұрышты қалай салу керек десе, онда AB[C]D дөңгелегін тұрғызып оның ішіне тік бұрыш бойынша қиылысатын АС және ВD диаметрлерін саламыз да AB, BC, CD және DA сызықтарын жүргіземіз. Сонда теңқабырғалы және тең бұрышты ABCD³⁶ төртбұрышын аламыз. Міне оның суреті [30 сурет].

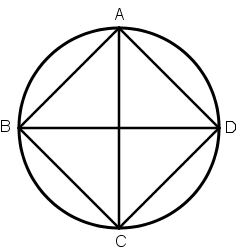
[30 сурет].

 

[ІV] Егер ол ABCD дөңгелегінің жарты диаметріне тең циркуль ашасын пайдаланып теңқабырғалы және тең бұрышты төртбұрышты дөңгелекке іштей қалай салу керек десе, онда АС диаметрін жүргіземіз. А нүктесін центр ретінде қабылдап циркуль ашасымен Е және G нүктелерін белгілейік та, Е мен G–ді қосайық. С нүктесін центр ретінде қабылдап АЕ қашықтықта H пен F–ті белгілейміз де H пен F–ті қосамыз. KG және IF сызықтарын жүргізейік, олар М нүктесінде қиылысады. М нүктесімен центрді қосып осы сызықты оның В мен D нүктелеріне дейінгі бағытында созайық. AB, BC, CD және DA сызықтарын жүргіземіз. Теңқабырғалы және тең бұрышты ABCD³⁷ төртбұрышы шығады. Міне оның суреті [31 сурет].

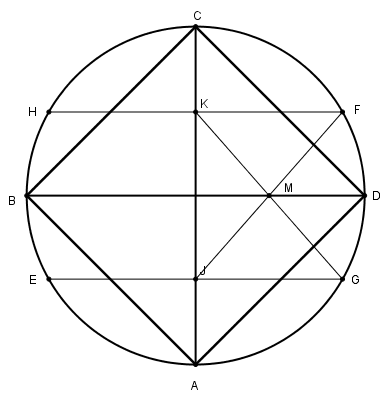
[31 сурет].

 

[V] Егер қаласаңыз А және С нүктелерін центр ретінде қабылдап, Е,G,H және F нүктелерін белгілейік. АС сызығын I және К нүктелерінде қиып өтетін EG және HF сызықтарын жүргізейік. Центрлері осы нүктелер болатын циркульдің ашасындай қашықтықта L және М нүктелерінде қиып өтетін екі дөңгелек сызайық. L және М–ді өзара қосайық та [LM]–ді В мен D нүктелеріне дейін созайық. AB, BC, CD және DA сызықтарын жүргізейік. Теңқабырғалы және тең бұрышты ABCD төртбұрышын аламыз. Міне оның суреті [32 – сурет].

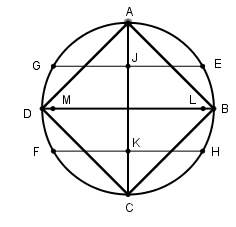
[32 – сурет].

 

[VІ] Егер қаласаңыз Е,G,H және F нүктелерін центр ретінде қабылдап, I және К нүктелерін қилысатын дөңгелектер салайық. IК сызығын жүргізейік, ол дөңгелекті В және D нүктелерінде қиып өтеді. Теңқабырғалы және тең бұрышты ABCD төртбұрышын аламыз. Міне оның суреті [33 – сурет].

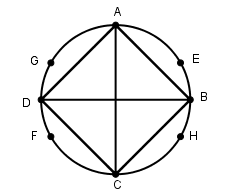
[33 – сурет].

 

[VІІ] Егер қаласаңыз А,F және C,G нүктелерін қосайық. А,F және C,G нүктелерін қосатын сызықтар М нүктесінде қиылысады. Оны центрмен қосып ол сызықты B мен D нүктелеріне дейін созайық. Міне оның суреті [34 – сурет].

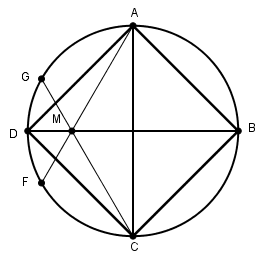
[34 – сурет].

 

[VІІІ] Шеңберге іштей сызылған бесбұрышты салу. Егер ол ABCD дөңгелегіне іштей сызылған тең қабырғалы және тең бұрышты бесбұрышты қалай салу керек десе онда D нүктесін центр ретінде алып онда ADC диаметрін жүргіземіз де D нүктесіне  DB перпендикулярын орнатамыз. AD–ны Е нүктесінде қақ бөліп Е нүктесін центр ретінде алып, ЕВ қашықтықта G нүктесін белгілейік те В нүктесін центр ретінде алып, ВG қашықтықта F нүктесін белгілейік. Сонда шөңгелектің бестен бір бөлігі BF доғасын аламыз. IF, IK, KH және HB доғаларын BF доғасына тең ете жүргізіп, FB, BH, HK, KI, IF сызықтарын сызамыз. Сонда тең қабырғалы және тең бұрышты BFIKH³⁸ бесбұрышын аламыз. Міне оның суреті [35 – сурет].

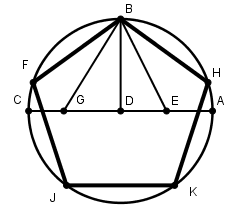
[35 – сурет].

 

[IX] Егер ол ABC дөңгелегіне іштей тең қабырғалы және тең бұрышты бесбұрышын егер D – дөңгелек центрі болса және  ашасы жарты диаметрге тең циркулмен қалай салу керек десе,  онда DA сызығына AB сызығына бесбұрыш салу кезінде салынған үшбұрышты  салайық. Бұл ADG  үшбұрышы болсын, ол ABC дөңгелегін C нүктесінде қияды. ABC доғасын B, H, E және C нүктелерінде төрт тең бөлікке бөліп, AC, CE, EH, HB және BA сызықтарын жүргізейік. Сонда тең қабырғалы және тең бұрышты ACEHBA³⁹ бесбұрышын аламыз. Міне оның суреті [36 – сурет].

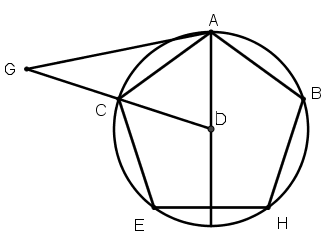
[36 – сурет].

 

  [X] Шеңберге іштей салынған бесбұрышты салудың басқа жолы. DA сызығына DA сызығына тең AE перпендикулярын тұрғызып, DA сызығын G нүктесінде қақ бөлейік, GE жүргізіп, AD сызығына тең GH сызығын салайық, оны F нүктесінде қақ бөліп, DA–ны I нүктесінде қиятын FI перпендикулярын тұрғызайық. I нүктесін центр ретінде қабылдап, DA қашықтықта M және L белгілейік. Сонда ML доғасы – дөңгелектің бестен бірі. Міне оның суреті [37 – сурет].

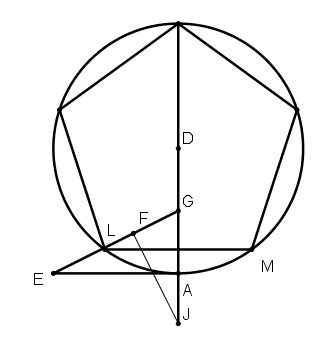
[37 – сурет].

 

  [XІ] Шеңберге іштей сызылған алтыбұрышты салу. Егер ол дөңгелекке іштей сызылған тең қабырғалы және тең бұрышты  алтыбұрышты қалай салу керек десе, онда A және C нүктелерінің әрқайсысын центр ретінде алып, AC диаметрін жүргізіп, диаметрдің жартысына тең қашықтықта B және H, E және G белгілейік. AB, BE, EG, CG, GH және HA сызықтарын жүргізейік. Тең қабырғалы және тең бұрышты ABECGH⁴⁰ алтыбұрышын аламыз. Міне оның суреті [38 – сурет].

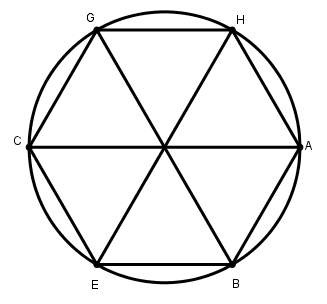
[38 – сурет].

 

[XІІ] Шеңберге іштей сызылған жетібұрышты салу. Егер ол дөңгелекке іштей сызылған тең қабырғалы және тең бұрышты жетібұрышты қалай салу керек десе, онда ADC диаметрін жүргіземіз де, AD, яғни жарты диаметр қашықтықта B және E белгілеп, BE жүргізейік, ол AC сызығын G нүктесінде қияды. B нүктесін центр ретінде қабылдап, BG қашықтықта H нүктесін белгілейік. Сонда BH доғасы – дөңгелектің дәл емес, жуық жетіден бірі. Сондықтан, егер ABCE дөңгелегін BH доғасына тең бөліктерге бөліп, бөлу орындарын өз ара қоссақ, онда тең қабырғалы және тең бұрышты FBHIKLM⁴¹ жетібұрышын аламыз. Міне оның суреті [39 – сурет].

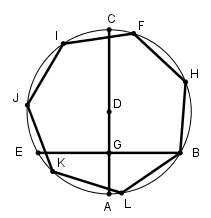
[39 – сурет].

 

[XIІІ] Шеңберге іштей сызылған сегізбұрышты салу. Егер ол дөңгелекке іштей сызылған тең қабырғалы және тең бұрышты  сегізбұрышты қалай салу керек десе, онда оған тең қабырғалы және тең бұрышты  төртбұрышты іштей саламыз да, әр доғаны қақ бөліп, бөлу орындарын жаңа нүктелерде түзу сызықтармен қосамыз. Тең қабырғалы тең бұрышты да сегізбұрыш аламыз. Міне оның суреті [40 – сурет].

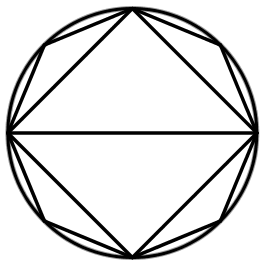
[40 – сурет].

 

[XIV] Шеңберге іштей сызылған тоғызбұрышты салу. Егер ол дөңгелекке іштей сызылған [тең қабырғалы және тең бұрышты] тоғызбұрышты қалай салу керек десе,  дөңгелекке  тең қабырғалы   үшбұрышты іштей  салып, әр доғаны тең үш бөлікке бөлеміз де, бөлу орындарын түзу сызықтармен қосамыз.  Тең қабырғалы [тең бұрышты да] тоғызбұрыш аламыз. Міне оның суреті [41 – сурет].

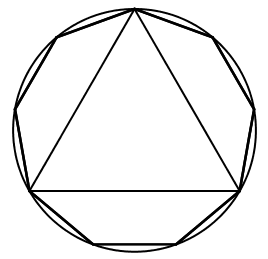
[41 – сурет].

 

[XV] Шеңберге іштей салынған онбұрышты салу. Егер ол дөңгелекке іштей салынған онбұрышты қалай салу керек десе, онда егер қаласақ, оған іштей бесбұрыш салып, доғаның әрқайсысын қақ бөлеміз [де, бөлу нүктелерін сызықтармен қосамыз], іштей сызылған онбұрыш шығады. Егер қаласақ, алдыңғы салынғанға ұқсас іштей бесбұрыш саламыз да, сосын бұрынғыдай DG сызығын [саламыз]. Бұл онбұрыштың хордасы. Шеңберді DG сызығына тең бөліктерге бөлейік те, бөлу орындарын өз ара түзу сызықтармен қосайық. Дөңгелекке іштей салынған тең қабырғалы [тең бұрышты да] онбұрыш⁴² шығады. Міне оның суреті [42 – сурет].

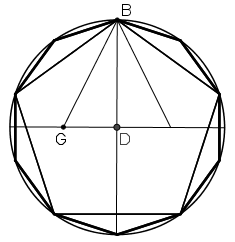
[42 – сурет].