Первоначальный текст

 Обоснования обучения

 Визуализация

[І]  Шығармашылықтың алдыңғы кітаптарында фигураларды қалай құру керектігін түсіндірдік, өзара іштей сызылған және өзара сырттай сызылған, олардың түрге бөлінуі және қолөнершілердің жиі пайдаланатындары. Математикадан білімі жеткіліксіз жандар үшін осының жеткілікті болатындығына үміттімін. Бұл кітапта мен қолөнершілер жиі қолданатын және көп сұрақ қойылатын фигуралардың бөліктері туралы баяндаймын. Бұл шаршыны (квадратты) бөліктеу, оларды құрастыру, [іштей сызылған фигураларды] тұрғызу. Біз пайдалануға қажетті ережелерді анықтадық. Қолөнершілердің пайдаланатын-дарының бәрі де осы кітаптағы мәселелер бойынша көптеген қателіктері бар бөліктеу мен құрастыру [пішіндеу] бірінсептері негізінде жасалады. Алла қалауына не керек болса соны қиындықсыз орындалатындай етіп баяндаймыз.

         Біз сандардың арасында квадраттысы да, квадратсызы да бар дейміз. Квадраттыларына келер болсақ, ол – егер саны өзіндей санға көбейтсек, онда, мысалы төрт пайда болады.  Ондай сан– екі. Себебі екіге екіні көбейтсек төрт болады. Мысалы, жиырма бес, өзіне өзін көбейткенде жиырма бес болатын сан табылады, ол– бес. Өзіне – өзін көбейткенге тең болатын бір сан квадратты сан деп аталады. Өзіне–өзі көбейтілетін сан сол санның түбірі немесе жағы деп аталады. Егер сан шаршылы болмаса, онда ол екі шаршылы саннан тұруы немесе екі шаршылы саннан тұрмауы мүмкін. Мысалы, он үш [саны] екі квадратты саннан: тоғыз бен төрттен тұрады. Тоғыз – квадратты және оның жағы – үш,  төрт– квадратты және оның жағы – екі. Мысалы, қырық бір [саны] екі квадратты тұрады: оның бірі – он алты, оның жағы – төрт, ал екіншісі – жиырма бес, оның жағы – бес.

Екі квадраттан тұрмайтын сан үшін, мысалы жеті үшін қосындысы өзіне тең болатын екі квадрат табылмайды, немесе он бір үшін де қосындысы өзіне тең болатын екі квадрат табылмайды.  Сондықтан да, егер әңгіме квадраттардан тұратын квадрат сандар туралы болса, онда квадраттарды тек квадрат болатын сандарға және квадраттардан құралған (тұратын) сандарға жіктеуге болады. Егер әңгімен квадраттың қанша квадраттың қосындысынан тұратындығы туралы немесе квадраттардан тұратын квадрат туралы болса, онда мен ол санды былай құрастырамын:  егер бұл сан шаршыны немесе екі шаршыдан тұратын болса, онда бұл істің қарапайым да жеңіл болғаны, ал егер бұл сан шаршыны да емес және квадраттардан құралмаған (тұрмайтын) болса, онда бұл істің қиын ауыр болғаны. Біз бұл араны егер Алланың қалауы болса осындағы әрбір түр үшін құрастыру жұмыстарын жүргізе аламыз.

  Егер тең шаршылардың шаршылар санынан құралған шаршыны бөлшектеу туралы сұрай қалса, онда шаршының әрбір жағын тең шаршыларға бөлеміз, олардың саны шаршылардың өзін құрастырған шаршыларға бөлінетін жағына тең. Бөлінетін жерлері арқылы сол жерлерге сәйкес келетін қарама–қарсы жаққа түзу жүргіземіз. Сонда берілген шаршыны оған ұқысас шаршыларға бөлшектейтін боламыз. Егер біз бір шаршыны тоғыз шаршыға бөлмек болсақ, онда шаршының бір қабырғасын тең үш бөлікке бөлеміз. Дәл осылай қалған қабырғаларды да тең үш бөлікке бөлеміз, бұл тоғыз санының түбірі болады. Әрі қарай қарсы жатқан қабырғадағы әрқайсысы арқылы түзу сызықтар жүргіземіз. Сонда шаршымыз тең тоғыз шаршыға бөлінеді. Міне оның суреті [116 – сурет].

[116 – сурет].

 

 [II] Дәл осылай, егер шаршыны төрт шаршыға бөлу керек болса, әр қабырғаны екіге бөлеміз – бұл төрт шаршының қабырғасы, қарама–қарсы бөліктерін қосамыз, сонда шаршы өзара тең бөікке бөлінеді.   Міне оның суреті [117 – сурет].

[117 – сурет].

 

[IІI] Шаршылардың жарты санынан шаршы тұрғызу туралы.

Егер біз шаршылардың көп шаршы сандарынан бір шаршы тұрғызғымыз келсе, онда қабырғасы осы шаршылардың қабырғасына тең бір шаршы аламыз. Оған мысал. Егер біз он алты басқа шаршылардан бір шаршы тұрғызғымыз келсе, онда берілген шаршыларды қатар тізіп, оған қалғандарын тіземіз, сонда бір шаршы шығады.   Міне оның суреті [118 – сурет].

[118 – сурет].

 

[IV] Екі шаршыдан тұратын шаршылардан шаршы тұрғызу туралы.

Егер біз осыны тұрғызғымыз келсе, онда екі шаршы санын алып, осы екі шаршыны қарастырамыз. Егер олар өзара тең болса, онда екі өзара тең шаршы тұрғызамыз. Олардың әрқайсысын диагоналды түрде бөлсек, төрт өзара тең шаршы шығады. Олардың диагоналдары ізделетін шаршының қабырғасына тең. Егер осы үшбұрыштарды бір–біріне өздерінің тік бұрыштары арқылы қосатын болсақ, шаршы шығады.

Оның мысалы. Егер біз екі басқа шаршыдан жаңа шаршы құрғымыз келсе, онда олардың әрқайсысын диагоналдары арқылы қиямыз, онда бүйір қабырғалары мен табаны тең төрт үшбұрыш пайда болады. Осы үшбұрыштарды тік бұрыштары жалғасатындай етіп қосамыз да қабырғасы үшбұрыштың табанына тең болатын шаршы тұрғызамыз. Міне оның суреті [119 – сурет].

[119 – сурет].

 

[V] Егер біз сегіз өзара тең шаршыдан жаңа шаршы тұрғызғымыз келсе, онда ол әрқайсысы төрт шаршыдан тұратын екі шаршы тұрғызайық. Сонан соң оларды диагоналдар арқылы бөлеміз; сонда төрт өзара тең үбұрыш пайда болады. Олардан жоғарыда айтылғандай етіп шаршы тұрғызамыз. Міне оның суреті  [120 – сурет].

[120 – сурет].

 

[VI] Егер саны екі өзара тең емес шаршылардан тұратын шаршылар берілген болса, онда әрқайсысының ұзындығы үлкен шаршының қабырғасына, ал ені кіші шаршы қабырғасына тең болатын екі тік төртбұрыш тұрғызамыз. Олардың әрқайсысын диагональ арқылы тең екі жартыға қиямыз; сонда өзара тең төрт үшбұрыш пайда болады, олардың қабырғалары шаршылардың диагоналдары ізделетін шаршының қабырғасына тең болады. Егер біз ортасына қабырғасы берілетін екі шаршының қабырғаларының айырымына тең шаршыны орналастырсақ және үшбұрыштың қабырғаларын оның қабырғаларына орналастырсақ, онда шаршылардан құрылған бір ғана шаршы шығады.

Оның мысалы. Егер біз тең қабырғалы және диагоналдары да тең он үш шаршыдан бір шаршы тұрғызғымыз келсе, онда бір шаршы бірлік шаршылардан тұрады, олардың саны тоғыз, бұл шаршының қабырғасы үшке тең; екіншісі төрт бірлік шаршыдан құралған, оның қабырғасы екіге тең. Бір қабырғасы үшке, екінші қабырғасы екіге тең екі тік төртбұрыш тұрғызайық. Әрқайсысы алты шаршыдан тұратын екі тік төтбұрыш пайда болады. Оларды диагонал бойынша қиямыз; сонда төрт үшбұрыш пайда болады, олардың ұзын катеті – үш, қысқасы – екі, ал гипотенузасы – он үштің түбірі [121 – сурет].

[121 – сурет].

 

Шаршылардан бірлігін бөліп алып, оны ортасына орналастырамыз да оған үлкен катеті бар үшбұрыштарды шаршының қабырғасына қосамыз. Олардан әрбір қабырғасы үшбұрыштың гипотенузасы болатын, яғни он үштің түбірі болатын шаршы құрылады⁵⁴. Міне оның суреті [122 – сурет].

[122 – сурет].

 

[VII] Егер біз өзара тең он шаршыдан бір шаршы тұрғызғымыз келсе, онда оны екі шаршыдан құрастырылған, оның  біреуі – тоғыз да түбірі үш, ал екіншісі – бір де түбірі бір. Бір қабырғасы үш те екінші қабырғасы бір болатын екі тік төртбұрыш тұрғызайық. Оларды диагоналдары арқылы тең екіге бөлейік. Оннан төрт шаршы қалады. Төрт шаршыдан бір шаршы тұрғызайық та оны ортасына орналастырып, оның қабырғаларына үшбұрыштарды жалғаймыз. Әрбір қабырғасы үшбұрыштың гипотенузасы болатын (яғни, онның түбірі)  шаршы пайда болады. Міне оның сурет [123 – сурет].

[123 – сурет].

 

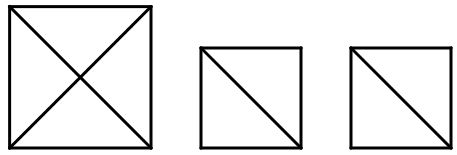
Тура осы сияқты он жеті өзара тең шаршылардан да шаршы тұрғызамыз [124 – сурет].

[124 – сурет].

 

Екі шаршыдан құрастырылған сан сәйкес келетін шаршылардан бір шаршы тұрғызу осы жоғарыдағыға негізделген.

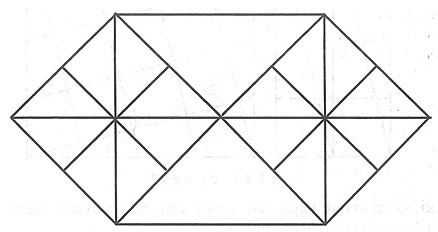
[VIII] Саны екі шаршы болатын шаршыларға бір шаршыны бөлу туралы. Бір шаршы берілген болсын. Егер біз екі шаршы санды шаршыға бөлеміз десек, онда ол сандарды қарастырамыз. Егер өзара тең болса, онда шаршыны диагоналдармен бөлеміз; онда төрт өзара тең үшбұрыштар пайда болады. Егер осылардың әрбір екеуін шаршының қабырғасы болатын қабырға бойымен қосатын болсақ, біз әрқайсысы екі үшбұрыштан тұратын екі шаршы тұрғызамыз. Міне оның суреті [125 – сурет].

[125 – сурет].

 

[ІХ] Егер біз шаршыларды алып, олардың әр қабырғасын тең бөліктерге бөлсек, олардың саны өзара тең шаршылардың қабырғасына тең болады да сонымен біз шаршыны ізделетін шаршыларға бөлеміз.

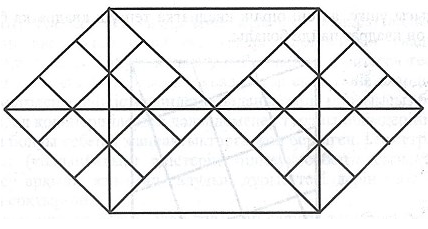
Оның мысалы. Егер біз бір шаршыны сегіз шаршыға бөлмек болсақ, онда оның диагоналдарын жүргіземіз; сонда төрт өзара тең үш бұрыш аламыз. Әрбір екі үшбұрыштан шаршы құрастырамыз; содан  екі шаршы аламыз. Әрі қарай екі шаршының әр қабырғасын екі тең бөлікке бөлеміз де бөліктің қарама–қарсы жақтарын түзу сызықтармен қосамыз (жалғаймыз). Сонымен біз сегіз өзара тең шаршылар тұрғызамыз. Міне оның суреті [126 – сурет].

[126 – сурет].

 

 [Х] Дәл осылай, егер біз шаршыны он сегіз өзара тең шаршыға бөлмек болсақ, оның диагоналдарын жүргіземіз, төрт бірдей өзара тең үшбұрыштар аламыз, осы сызбада екі шаршы тұрғызамыз. Әрі қарай екі шаршының әр қабырғасын үш тең бөлікке бөліп, бөлінген жақтарын қосамыз. Тең қабырғалы он сегіз шаршы пайда болады. Оның сурет мынау [127 – сурет].

[127 – сурет].

 

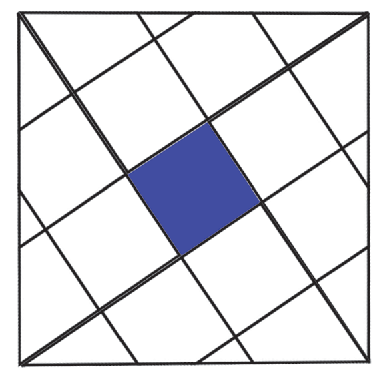
[ХІ] Бір шаршыны саны екі өзара тең емес шаршыдан тұратын шаршыларға бөлу туралы. Бір шаршыны екі бірдей әртүрлі шаршыдан тұратын шаршылар санына бөлу үшін шаршының бір қабырғасын тең бөліктерге бөлеміз, олардың саны үлкен шаршы қабырғасына тең, ал берілген сан солардан құралған. Әрі қарай берілген шаршының әр қабырғасынан оның төбесінен бір бағытта кіші шаршы қабырғасына тең сызықты өлшеп аламыз да шаршының әр бұрышынан қарама–қарсы жатқан бөлшектеу орнына қарай түзу сызықтар жүргіземіз; сонда ортасында шаршы және сол шаршыны қоршаған төрт үшбұрыш пайда болады.

Бұл шаршы шаршылардың қабырғаларының айырымынң шаршысына тең. Осы шаршының қабырғаларын айырымға тең болатын бөліктер санына бөлеміз; сонда айырым шаршысына тең шаршылар саны шығады. Ал үшбұрыштарға келер болсақ, егер оларды екеуден біріктіретін болсақ, онда ұзындығы үлкен шаршы қабырғасына тең болатын тік төртбұрыштар алынады, ал оның ені екі шаршының ең кішісінің қабырғасына тең болады. Сондықтан  да егер осы екі тік төртбұрышты тұрғызып, олардың қабырғаларын шаршылардың қабырғаларының санына тең бөлікке бөлетін болсақ, онда қалған ізделетін шаршылар алынады. Оған мысал. Егер біз бір шаршыны он шаршыға бөлмек болсақ, онда онның екі шаршыдан – тоғыз бен бірден тұратындығын, біреуінің қабырғасы – үш те, екіншісінің қабырғасы – бір екендігін аңғарамыз. Шаршының бір қабырғасын тең үш бөлікке бөліп, әр қабырғасына бірге тең кесінді саламыз, қарсыдағы бұрыштардан бөліну нүктелеріне  түзу сызықтар жүргіземіз; сонда ортада бір шаршы және оны қорша орналасқан төрт үшбұрыш пайда болады. Міне оның суреті [128 – сурет].

[128 – сурет].

 

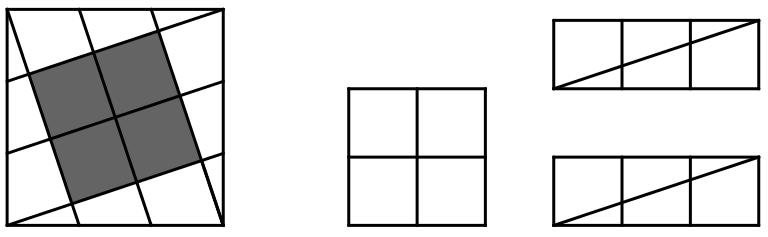
Әрі қарай ортадағы шаршының қабырғасын екіге бөлеміз, яғни онды құратын шаршы қабырғаларының айырымына бөлеміз. Бөліну нүктелерінен параллель сызықтар жүргіземіз. Бөліну нүктелерінен параллель сызықтар жүргіземіз: ортада төрт шаршы пайда болады. Әрбір екі үшбұрыштан ұзындығы – үш, ал ені – бір болатын тік төртбұрыштар тұрғызамыз да оларды үш шаршыға бөлеміз; сонда он шаршы пайда болады.

[ХІІ] Дәл солай, егер біз бір шаршыны жиырма шаршыға бөлмек болсақ, онда жиырмамыз екі шаршыдан тұрады: біреуі он алты [оның қабырғасы – төрт], екіншісі – төрт [оның қабырғасы – екі]. Шаршының қабырғасын тең төрт бөлікке бөлеміз, қабырғаларына екінші шаршының қабырғасына тең сызықты орналастырамыз да бұрыштардан бөліну нүктелеріне сызық жүргіземіз; сонда қабырғасы екі шаршы қабырғаларының айырымы болатын және оны қоршаған төрт үшбұрыш пайда болады.

Шаршыны қоршаған осы үшбұрыштардың әрбір екеуінен ұзындығы – төрт, ені екі болатын тіктөртбұрыш құрамыз. Ортада тұрған шаршыны төрт шаршыға жіктейміз, ал екі тік төртбұрышты – он алты шаршыға жіктейміз. Сонда жиырма шаршы алынады. Міне оның суреті [129 – сурет].

[129 – сурет].

 

[ХІІІ] Саны екі шаршыдан тұратын шаршылдарды бөлшектеу әдістері, егер шаршылардың саны екі шаршыдан тұрмайтын болса, оларды бөлшектеуді шаршы түзуге ауыстыруға болмайды. Көптеген геометрлер мен қолөнершілер осы шаршыларды тұрғызу және оларды құрастыру жолында қателіктер жіберді: геометрлер тәжірибенің аздығынан, ал қолөнершілер дәлелдеуге қажетті білімдерінің  жетіспеушілігінен. Себебі, геометрлер тұрғызудың тәжірибелік әдістерін білмейді, сондықтан да оларға сызықтарда дәлелдеу арқылы жуықтап тұрғызудың дұрыс тәсілдерін табу қиынға түсті.

Қолөнершілерге келер болсақ, иолар жуықтап тұрғызу жолын тапқанда, біздің сезінетін және көретін нәрселерімізді алады, сызықтардың көмегімен дәлелдеуге және геометрлерге көңіл аудармайды. Теориялық пайымдаулар арқылы бірнәрсені дәлелдеуге қол жеткізген адам, оның тұрмыста қаншалықты ақиқаттылығын тексермейді. Қолөнершілердің білгенінің бәрі де геометрлер дәлелдеген шындық екендігіне мен күмәнданбаймын және дәлелдеулер осының дұрыс екендігін көрсетеді. Бірақ қолөнерші мен жерөлшегіш істің маңыздылығын қарастырады, оны қалай дәлелдеуді ойламайды, сондықтан да олар қате жібереді. Геометрлерге келсек, оларға біздің дәлелдеу арқылы не алғымыз келетіндігі түсінікті, егер олар қолөнершілермен жер өлшегіштердің нені пайдаланатындығын дәлелдейтін болса. Геометрлерге, пішіндерді бөлшектеу мен сызықтарды көбейту туралы сұрақ қойғанда олар әбігерге түседі де оларға ойлануға көп уақыт керек болатындығы тән. Кейде бұл оларды шешімге жақындатады, кейде алыстатады. Мен қолөнерршілер мен жер өлшегіштер қатысқан кейбір тартыстарға қатыстым. Олардан үш шаршыдан бір шаршы тұрғызу туралы сұралды. Геометрге келсек, ол үш шаршыдан тұратын шаршының қабырғасын жеңіл табатын. Бірақ ол қолөнершілерді қанағаттандырмады, себебі оған бір ғана шаршы құралатын бұл үш шаршыны бөліктерге бөлу қажет, мұндай нәрсе екі және бес шаршы жағдайында орын алған.⁵⁵ Қолөнершілер болса, бұл үшін бірнеше тәсілдер ұсынды. Олардың кейбіреулері үшін дәлелдеулер келтірілді, ал қалғандары жалған болып шықты. Дәлелдеуге болмайтындары шындыққа өте жақын болып көрінді және осы тұрғызуларға қарап тұрған адам оларды дұрыс деп ойлайды.

Олардың қайсысы дұрыс, қайсысы бұрыс екенін білу үшін сол тәсілдерді келтіреміз. Біз көзге сүйене алмаймыз, себебі көз, егер осыны Алла қаласа, бұл тәсілдердің қайсысы жалған екендігін айтуға көзіңіз жақсы көмекші бола алмайды.

Кейбір қолөнершілер бір шаршыны ортаға қояды, екіншісін диагональ арқылы бөледі де осы екі бөлікті шаршының қабырғаларына орналастырады. Үшінші шаршының ортасын бір диагоналда жатпайтын төбесімен екі сызық арқылы қосады, да шаршының ортасын екі сызық және шаршының қабырғасы арқылы жасалған үшбұрышқа қарсы жатқан қабырғаның ортасымен қосады. Бұл шаршы екіге трапеция мен үшбұрышқа бөлінеді. Бұл үшбұрышты бірінші шаршының төменгі қабырғасына орналастырады, ал екі трапецияны оның жоғарғы қабырғасына олардың ұзын қабырғалары ортада болатындай етіп орналастырады. Мына суретте келтірілгендей шаршы пайда болады [130 – сурет].

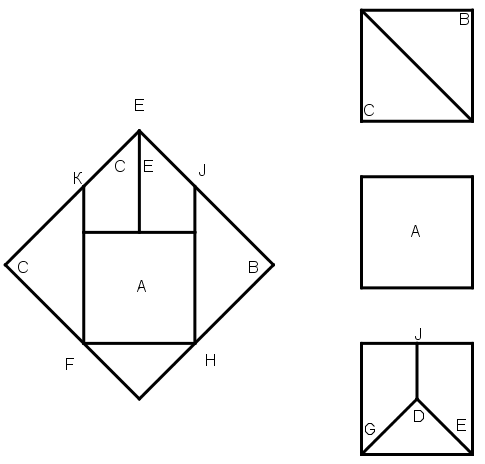
[130 – сурет].

 

Ол тұрғызған суретке келер болсақ, мұнда бір қулық бар. Геометрия өнерін үйренбеген адам бұл тұрғызуды дұрыс көреді, егер оны барынша жан–жақты қарайтын болсақ, онда бұл тәсіл дұрыс болмай шығады. Бізге дұрыс болып көрінсе де, бірақ бұрыштар мен қабырғалардлың теңдігіне  қатыстысы оның әрбір бұрышы тік, ал қабырғалары тең, сондықтан да бұл тәсіл дұрыс сияқты көрінеді. Шаршының бұрыштар саналатын С, B, D үшбұрыштарының әрбір бұрышы тік, ал төртінші бұрыш әрқайсысы– түзудің жартысы, яғни екі трапецияның Е және G бұрыштарынан болатын екі бұрыштан тұрады. Қабырғаларына келер болсақ, олар – түзу сызықтар және өзара тең.

Бұл қабырғалардың әрқайсысы шаршының қабырғасынан тұрады. Сондықтан да олар өзара тең. Бұл тұрғызуда олардың түзу екендігі тұрғысында болса, онда бұл дәлелденген, себебі түзулердің қиылысу нүктесіндегі барлық бұрыштардың қосындысы екі тік бұрышқа тең және Н нүктесіндегі үш бұрыштың қосындысы да екі тік бұрышқа тең, себебі бұл бұрыштардың біреуі шаршының бұрышы, ал қалған екі бұрышы – үшбұрыштардың бұрышы, оның әрқайсысы – тік бұрыштың жартысы. F бұрышы да сондай. І бұрышына келер болсақ, ол екі бұрыштан тұрады, оның бірі – үшбұрыштың бұрышы, яғни тік бұрыштың жартысы, ал басқа бұрышы – трапеция бұрышы, яғни бір жарым тікбұрыш. Бұл жағдай К нүктесіндегі бұрыштарға да қатысты. Сондықтан да егер бұрыштар тік болса, ал қабырғалары өзара тең түзу сызық болса, онда әр адам үшін үш шаршыдан тұратын бір шаршы шығатындығы айдан анық та, ол қай жерде қате жібергендігін білмей әлек. Дегенмен, белгілі болғандай бір шаршының әрқайсысы шаршылардың біріні қабырғасына және оның диагоналының жартысына тең болғандығын байқаймыз. Бірақ үш шаршыдан түұратын шаршының қабырғасы бұл шамаға тең болуы мүмкін емес, себебі ол шамадан үлкен болуға тиіс. Мейлі, шаршының әр қабырғасы екі шынтақ болсын; онда әрбір сауатты адамға үш шаршыдан тұрғызылған шаршының қабырғасы шамамен он жеті шынтаққа және оның үштен біріне тең, ал бұл шаршының қабырғасы – он жеті және жетіден бірінің жартысына тең болатындығы бесенеден белгілі.

Бұл шаршылардың арасында үлкен айырмашылық бар. ВС шаршысын екіге бөлгенде оның әрбір жартысын HI  мен FK сызықтары арқылы ВС шаршысының жартыларынан бөлінген шаршының қабырғаларына қойғанда бұл мүмкін емес, себебі ВС шаршысының диагоналы үшінші шаршының қабырғасына тең емес. HI сызығы ВС шаршысының қабырғасына тең және оның екінші қабырғасының жартысына тең, бірақ ол бұл қабырғадан кіші, себебі ВС шаршысының диагоналы шамамен он төртке және жетіден бірге тең, ал HI–сызығы он беске тең. Осымен бұл бөлшектеу мен тұрғызудың жарамсыздығы дәлелденді⁵⁶.

[XIV]  Кейбір адамдар бұл шаршыларды басқа тәсілдер арқылы бөлшектейді, бірінші бөлшектеуге қарағанда бұл бөлшектеудің жарамсыздығы айқын көрінеді. Олар екі шаршының диагоналі ортасынан осы шаршы қабырғасына тең кесіндіні бөліп алып,  төбелерден диагоналдар бойынша төрт үшбұрыш кесіп шығарады. Сонымен екі шаршыдан төрт әрқабырғалы бесбұрыш пен төрт үшбұрыш пайда болады. Содан соң олар әрбір бесбұрышты үшінші шаршының қабырғасына орналастырды және төрт бұрышты төрт үшбұрышқа орын табылады екен. Осы үшбұрыштарды сол орындарға көшіріп, үш шаршыдан тұратын шаршы алады. Міне оның суреті [131 – сурет].

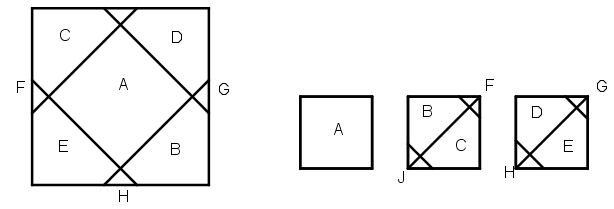
[131 – сурет].

 

Бұл геометрия мен дәлелдеулермен айналыспайтындар үшін дұрыс болып көрінуі мүмкін, ал олар ойлана бастағанда бұл тәсіл жарамсыз болып шығады, себебі олардың шаршы төбесіндегі бос орындарға шығарған үшбұрыштар ол орындардан үлкен, себебі ол бос орындар екі қабырға арасында орналасқан, ал үшбұрыштың әр қабырғасы шаршыдан қиылған үшбұрыштың гипотенузасының жартысына тең. Сондықтан ол бұл бұл үшбұрыштың қабырғасы бос орындағы үшбұрыштың гипотенузасына тең.

[XV] Шаршыны біз көрсеткен қажетті дәлелдемелер арқылы анықталған дұрыс тәсіл бойынша бөлу туралы әңгіме етсек, онда үш шаршының екі шаршысын диагоналдары бойынша бөлеміз (төрт тіктөртбұрыш пайда болады), осылардың әрқайсысының қабырғасын үшінші шаршының қабырғаларына орналастырамыз, сонымен қатар үшбұрыштың тікбұрыштың жартысына тең болатын бұрышын шаршының бір бұрышының үстіне, ал үшбұрыштың гипотенузасын шаршының қабырғасына орналастырамыз; сонда үшбұрыштың екінші бұрышы жағындағы бөлігі сыртқа шығып тұрады. Үшбұрыштың тікбұрыштарының төбелерін түзу сызықтармен қосамыз; сонда ізделуші шаршының қабырғасы анықталады. Үлкен үшбұрыштың әрқайсысынан кіші үшбұрыш бөліп аламыз да оны үшбұрыштың қабырғасының екінші жағындағы жетіспей тұрған орынға орналастырамыз.

Осының мысалы. Егер біз бұны ABCD, EPGH және FJKL үш тең шаршылардан салмақшы болсақ, онда осы шаршылардың екеуінің BD және PG диагоналдарын сызып екі бөлікке бөлеміз, бұларды үшінші шаршының қабырғаларының үстіне орналастырамыз. Содан соң үшбұрыштардың тікбұрыштарының төбелерін ВО, GP, PD және DB сызықтарымен қосамыз. Үшбұрыштың қабырғасының сыртында үлкен үшбұрыштың әрбір қабырғасының бойында осы үлкен үшбұрыштан бөлініп алынған үшбұрышқа тең кішкене үшбұрыш бар. Сондықтан ВМ үшбұрышы MFG үшбұрышына тең, себебі С бұрышы тікбұрыштың жартысына тең және MFG бұрышы да тікбұрыштың жартысына тең, М бұрышының бойындағы үшбұрыштың екі вертикаль бұрышы да тең, ВС қабырғасы FG қабырғасына тең, сондықтан бір үшбұрыштың өзге қабырғалары екінші үшбұрыштың басқа қабырғаларына тең және бір үшбұрыш екінші үшбұрышқа тең. Сондықтан, егер біз ВСМ үшбұрышын MFG үшбұрышының орнына орналастырсақ, BG сызығы үш шаршыдан құралған шаршының қабырғасы болады. Осы тәсіл дұрыс әрі ақиқатқа барынша жуықтау, себебі бұл дәлелдемелер арқылы анықталған⁵⁷. Міне оның суреті [132 – сурет].

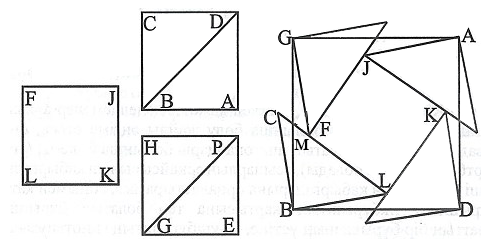
[132 – сурет].

 

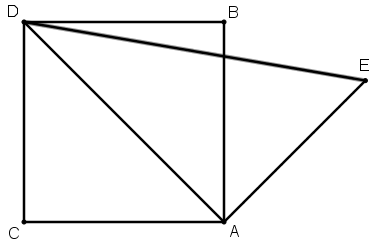
[XVI] Егер де геометрден саны көп немесе саны аз шаршылардан шаршы салу туралы сұраса, онда ол шаршысы осы шаршыларға тең сызықты табады да шаршыларды бөлуге мән бермейді. Сондықтан одан үш шаршыдан шаршы салу туралы сұралса, онда ол бір шаршының диагоналын сызады да, диагонал сызығының бір ұшынан оған шаршының қабырғасына тең болатын перпендикуляр тұрғызады, перпендикулярдың ұшын диагоналдың басқа ұшымен түзу сызықпен қосады; сонда үш тең шаршыдан құралған шаршының қабырғасы анықталады.

Осының мысалы. Біз әрқайсысы ABCD шаршысына тең үш тең шаршы салмақшымыз. AD диагоналын сызамыз. Сонда AD – екі шаршыдан салынған шаршының қабырғасы болады. Одан соң AD сызығына А нүктесінде АЕ перпендикулярын тұрғызамыз да, Е–ні D–мен қосамыз. Сонда ED сызығы – әрқайсысы ABCD шаршысына тең үш тең шаршының қабырғасы болады.

Геометр осы сызықты анықтаған соң, ол осы шаршыларды бөлу тәсілін іздемейді, ED сызығының бойына үш шаршыға тең шаршы салуды ғана ойлайды. Міне оның суреті [133 – сурет].

[133 – сурет].

 

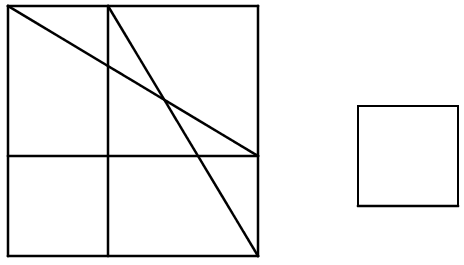
Егер біздің үштен көп немесе одан аз шаршылардан құралған шаршы салғымыз келсе, дәл осы секілді салуды жүзеге асырамыз⁵⁸.

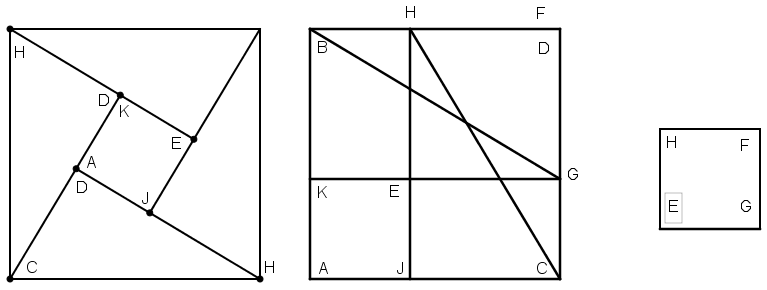
[XVII] Қабырғаларының шамасы белгісіз әр түрлі екі шаршыдан шаршы салу туралы. Егер біз баяндап өткен шаршылар салу жұмысына ұқсас салу орындалса, біз шаршы немесе әр түрлі екі шаршы салудың жалпы әдісіне тап боламыз, бұған екі шаршыны қосу кезінде сүйенуімізге тура келеді. Егер біз үш шаршыдан шаршы салмақ болсақ, онда біз екі шаршыдан шаршы саламыз. Кіші, яғни үшінші шаршымен салыстырғанда үлкен шаршы жасаймыз. Егер біз әлгілерден шаршы салсақ, ізделуші шаршы пайда болмақ. Егер біз осы шаршыны салмақ болсақ, онда кіші шаршының бір бұрышы үлкен шаршының бұрышының біреуімен беттесетін етіп, кіші шаршыны үлкен шаршының үстіне беттестіреміз, ал екі қабырғасын екі қабырғаның үстіне дәл етіп орналастырамыз. Содан соң кіші шаршының қабырғаларын үлкен шаршының қабырғаларымен қиылысқанша созамыз да, үлкен шаршыдан кіші шаршының қабырғасындай, үлкен шаршының екінші қабырғасына параллель тіктөртбұрышты бөліп шығарамыз. Сонда үлкен шаршының ішінде тіктөртбұрыш қалады. Тіктөртбұрыштан үлкен шаршыдан бөлініп алынған, кіші шаршымен бірге басқа бір тіктөртбұрыш құрайтын бөлікті қиып аламыз. Сонда үлкен шаршыда кіші шаршы қана қалады. Оны сақтап қоямыз. Одан соң екі тіктөртбұрышты олардың диагоналдарымен қиямыз; сонда төрт үшбұрыш пайда болады. Бұлардың гипотенузасы ізделуші шаршының қабырғасы болып табылады. Сонан соң, сақталып қойылған кіші шаршыны ортаға орналастырамыз да оған төрт үшбұрышты біріктіреміз, бұлардың әрқайсысы оның бір қабырғасына шаршының тікбұрышы үшбұрыштың тік бұрышына қабысатындай болып орналастырылады. Сонда екі шаршыдан құралған үлкен шаршы пайда болады. Міне оның суреті [134 – сурет].

[134 – сурет]

 

Бұның дұрыстығын дәлелдеу үшін ABCD үлкен шаршысы мен GEHF кіші шаршысын саламыз. Кіші шаршыны үлкен шаршының үстіне былайша саламыз, F бұрышы D бұрышының үстіне, GF сызығы CD сызығының үстіне, ал HF сызығы BD сызығының үстіне түсетіндей болып орналастырылады. Үлкен шаршыны НЕ қабырғасымен J нүктесінде қиямыз; сонда үлкен шаршыдан HJAB тіктөртбұрышы бөлінеді. HJAB тіктөртбұрышынан JEGC тіктөртбұрышына тең КВНЕ тіктөртбұрышын қиып алып тастаймыз. Үлкен шаршыдан кіші AKEJ шаршысы қалады. Будан соң екі тіктөртбұрыштан төрт үшбұрыш құраймыз, яғни тіктөртбұрыштарды диагоналдарымен қиямыз. Осының нәтижесінде төрт үшбұрыш және кіші шаршы пайда болады. Кіші шаршыны ортаға орналастырып, оның айналасына төрт үшбұрышты DCH үшбұрышының С бұрышы К бұрышына, ал DC қабырғасы КА қабырғасына, CHD үшбұрышының D бұрышы А бұрышына, ал CD сызығы AJ қабырғасына жанастырып орналастырамыз. Қалған екі үшбұрышты да осы екі үшбұрыш секілді жанастырамыз. Сонда, біздің бұрын сызғанымыздай сурет [135 – сурет] пайда болады:

 

[135 – сурет].

 

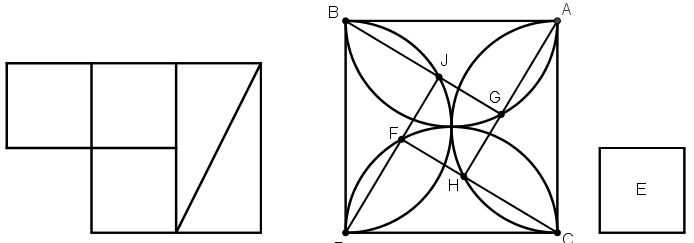
[XVIII] Бір шаршыны шаршылардан құралмаған шаршыларға бөлу туралы. Біз әрқайсысының қабырғаларының шамасы белгілі шаршыны үлкен және кіші шаршыларға осылайша бөлуді түсіндірген болатынбыз. Егер де қабырғалардың шамасы беймәлім болса, онда шаршыны екі шаршыға бірнеше рет бөлуге тура келеді, яғни үлкен шаршыдан белгілі шамадағы кіші шаршыны қалай бөлуге болатыны және шаршының қалған бөлігінен басқа шаршыны қалай құрастыруға болатыны жайлы сұралатын басқа мәселені шешуге тура келеді. Егер біздің айтқанымыздай істейтін болсақ, онда жоғарыда баяндалған салуға көңіл аударуымыз керек.

Үлкен шаршы, мысалы, ABCD шаршысы, кіші шаршы, мысалы, Е шаршысы берілген болсын. Үлкен шаршыдан кіші шаршыға тең шаршыны қалай салу және қалған бөліктерден басқа шаршы қалай құрастыру айтылған болатын, сондықтан жоғарыда айтылғанды істейміз. Егер біз ABCD шаршысынан Е–ге тең шаршы бөліп алмақ және қалған бөліктерден басқа шаршы салмақ болсақ, онда ABCD шаршысының әрбір қабырғасына сырттай жарты дөңгелек сызамыз. А, В, С және D бұрыштарының әрбір төбесін дөңгелектің ортасы ретінде алып, Е шаршысының қабырғасындай аралықта жарты дөңгелек бойынан G, Н, F және J нүктелерін белгілейміз де AGH, BJG, DFJ және CHF сызықтарын сызамыз. Сонда ортасында шаршы пайда болады, ал СН, DF, BJ, AG сызықтарының әрқайсысы кіші шаршының қабырғасына тең. Сондықтан төрт үшбұрыш және кіші шаршы пайда болады. Әрбір екі үшбұрыштан тіктөртбұрыш құрастырамыз, ортада орналасқан шаршыны осы, тіктөртбұрыштың бірінің үстіне бір–біріне тақап бастыра саламыз. Сонда тіктөртбұрыштың ұзындығының шаршының ұзындығынан артылған бөлігі екі тіктөртбұрыштың қиысуы болып табылатын екі шаршының кішісін құрайды. Осы шаршыны ескермей тастасақ үлкен шаршы пайда болады. Міне оның суреті [136 – сурет].

[136 – сурет].