Первоначальный текст

 Обоснования обучения

 Визуализация

[І] Егер ол ABCD жазық фигурасын оның бұрыштарының бірі арқылы өтетін сызықпен қалай қақ бөлу керек десе, онда A бұрышын аламыз да E нүктесінде қиылысатын AC және BD сызықтарын жүргіземіз. Онда егер BE сызығы ED сызығына тең болса, онда AC сызығы ABCD фигурасын қақ бөледі⁵⁰. Міне оның суреті [82 – сурет].

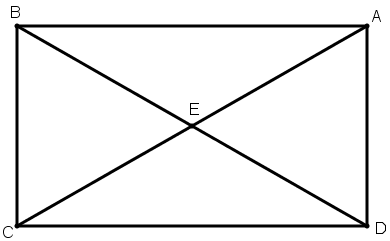
[82 – сурет].

 

[ІІ] Егер BE   ED–ға тең болмаса, онда BD–ны G нүктесінде қақ бөлеміз, ол арқылы AC сызығына параллель GH сызығын жүргіземіз, A–ны H–пен қосамыз. Сонда ABCD фигурасы AH сызығымен қақ бөлінеді. Міне оның суреті  [83 – сурет].

 

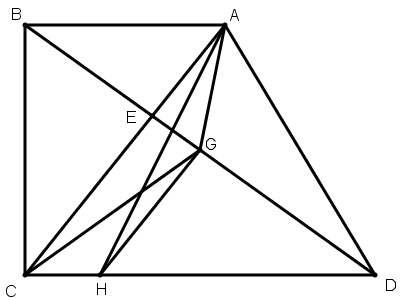
[83 – сурет].

 

[ІІІ] Егер ол ABCD жазық фигурасын фигураның бір қабырғасындағы E нүктесі арқылы өтетін сызықпен қалай тең екіге бөлеміз десе, онда ABCD фигурасын B нүктесі арқылы өтетін сызықпен тең екіге бөлеміз, ІІ–сөйлемде дәлелденгендей бұл – BG сызығы. EG мен EC–ны қосамыз. Егер EG сызығы BC сызығына параллель болса, онда EC сызығы ABCD фигурасын қақ бөледі. Міне оның суреті  [84 – сурет].

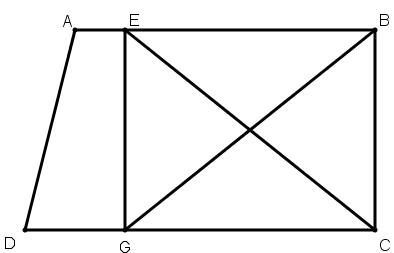
[84 – сурет].

 

[IV] Егер EG сызығы BC сызығына параллель болмаса, онда B нүктесінен EG сызығына параллель BH сызығын жүргіземіз, онда ол фигура ішінде немесе сыртында болады. Бастапқыда ол фигура ішінде болсын. E–ні H–пен қосамыз. Сонда EH сызығы ABCD фигурасын қақ бөледі. Міне оның суреті  [85 – сурет].

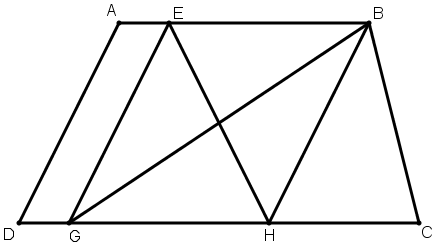
[85 – сурет].

 

[V] Енді ВН сызығы ABCD фигурасының сыртында болсын. DC сызығын ВН–пен Н нүктесінде қиылысқанша жалғастырамыз, Н нүктесінен ЕС сызығына параллель HF сызығын жүргіземіз және E–ні F–пен қосамыз. Сонда EF сызығы ABCD фигурасын қақ бөледі. Міне оның суреті [86 – сурет].

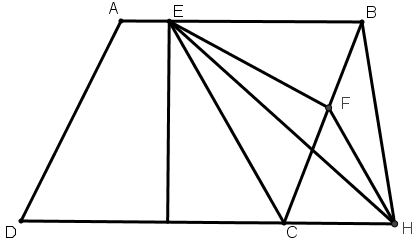
[86 – сурет].

 

[VI] Егер ол ABCD трапециясын CD сызығына параллель сызықпен қалай қақ бөлуге болады десе, онда AC және BD сызығын E нүктесінде қиылысқанға дейін созамыз, E нүктесінде BE сызығына тең,  BD сызығына перпендикуляр EG сызығын саламыз. DG–ды қосамыз  және DG сызығын H–қа дейін GH GD–дің жартысына тең болатындай етіп созамыз. HD–ға HFD жарты дөңгелек жүргіземіз, DH–қа перпендикуляр GF тұрғызамыз, GF сызығына тең EI–ді аламыз және CD–ге параллель IK сызығын жүргіземіз. Сонда ABCD трапециясы KI сызығымен қақ бөлінеді. Міне оның суреті [87 – сурет].

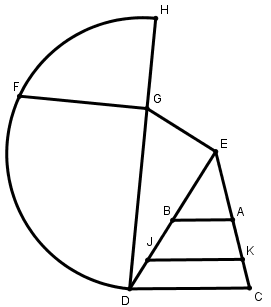
[87 – сурет].

 

 [VII] Егер ол ABCD паралелограммын қандай да бір қабырғасындағы нүкте арқылы өтетін сызықпен қақ бөлуге болады десе: мысалы, E нүктесі арқылы CD сызығы, онда AB сызығында DE сызығына тең  AG сызығын кесіп алып GE сызығымен қосамыз. Сонда AGEC трапециясы BGED трапециясына тең болады. Міне оның суреті [88 және 89 – суреттер].

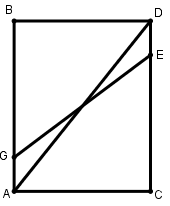
 [88 – сурет].

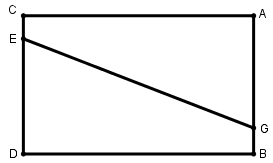
[89 – сурет].

 

[VIII] Егер ол AD кесіндісінен өтетін  нүкте арқылы ABCD параллелограмынан сызықпен қалай бөліп алуға болады десе, онда үштен бір бөлігін бөліп аламыз. AD сызығындағы E нүктесі белгіленген болсын, E нүктесі арқылы AB сызығына параллель EG сызығын жүргіземіз. Егер AE– кесіндісі AD сызығының үштен бірін құрайды деп есептесек, онда мен ABCD фигурасынан оның үштен бірі ABEG фигурасын бөліп алдым. Міне оның суреті [90 – сурет].

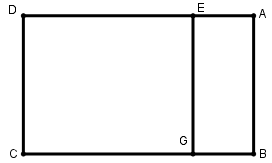
[90 – сурет].

 

[IX] Егер АЕ АD–ның үштен бірі болмаса, онда АD–ның үштен бірі АН–ты аламыз. Онда Н нүктесі АЕ сызығында немесе DЕ сызығында жатады. Егер Н нүктесі бірінші суреттегідей АЕ сызығында жатса, онда АВ сызығына параллель НІ сызығын жүргіземіз, F нүктесінде қақ бөлеміз, ЕFG жүргіземіз. GIF үшбұрышы  HFE үшбұрышына тең. Онда ABGE  ABCD фигурасының үштен бірі. Міне оның суреті [91 – сурет].

[91 – сурет].

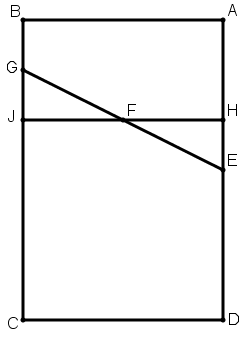
[X] Енді Н нүктесі ED сызығында жатсын. HI сызығын F нүктесінде қақ бөлеміз, EF сызығын жүргіземіз және оны G нүктесіне дейін созамыз. Сонда AEGB трапециясы ABCD–ның үштен бірі. EH сызығы  BI сызығына тең болсын не тең болмасын. Егер тең болса, В нүктесін Е нүктесімен қосамыз. Сонда ABE үшбұрышы  ABCD фигурасының үштен бірі, AHB үшбұрышы  ABCD фигурасының үштен бірінің жартысы.

[XI] Егер EH сызығы IB сызығынан қысқа болса, онда EH сызығына тең GI сызығын сызамыз және E нүктесін G нүктесімен қосамыз, сонда ABFH – ABCD фигурасының үштен бірі. Міне оның суреті [92 – сурет].

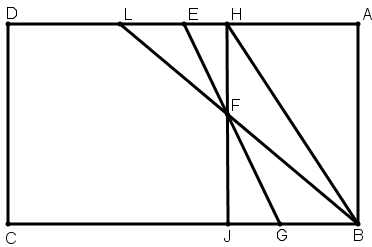
[92 – сурет].

 

[XII] Егер EH сызығы IB сызығынан ұзынырақ болса, онда IB сызығын FB сызығы EH сызығының артығына тең болатындай етіп, F нүктесіне дейін созамыз (IB сызығының үстінен), E және B нүктелерін қосамыз. BE сызығына параллель FG сызығын жүргіземіз және GE–ні қосамыз. Сонда AGE үшбұрышы – ABCD фигурасының үштен бірі болады. Міне оның суреті [93 – сурет].

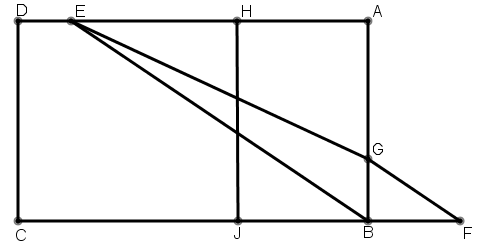
[93 – сурет].

 

[XIII] Егер ол ABCD трапециясын AD қабырғасында жатқан нүктеден, мысалы E нүктесінен өтетін сызық арқылы қалай қақ бөлуге болады десе, онда BC сызығын G нүктесінде қақ бөліп, GE–ні қосамыз. Онда егер AE сызығы ED сызығына тең болса және  BG сызығы GC сызығына тең болса, онда EG сызығы ABCD фигурасын қақ бөледі. Міне оның суреті [94 – сурет].

 

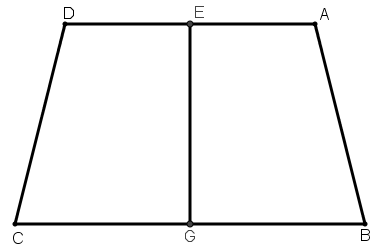
[94 – сурет].

 

[XIV] Егер де AE сызығы ED сызығына тең болмаса, онда AH сызығын HD сызығына тең болатындай етіп саламыз. Сонымен қатар BG сызығы GC сызығына тең. H және G нүктелерін қосамыз, HG сызығын F  нүктесінде қақ бөлеміз және EFK сызығын жүргіземіз. Онда EK сызығы трапецияны қақ бөледі. Міне оның суреті [95 – сурет].

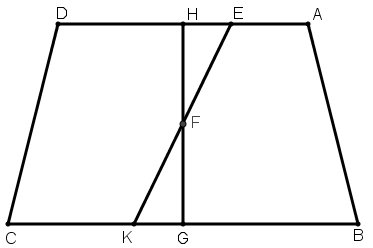
 [95 – сурет].

 

[XV] Егер ол ABCD параллелограмын оның сыртында жатқан нүктеден, мысалы E нүктесінен, өтетін сызық арқылы қалай қақ бөлу керек десе, онда AD–ны қосамыз, AD сызығын G нүктесінде қақ бөліп, EGH сызығын жүргіземіз. Сонда EGH сызығы ABCD фигурасын қақ бөледі. Міне оның суреті [96 – сурет].

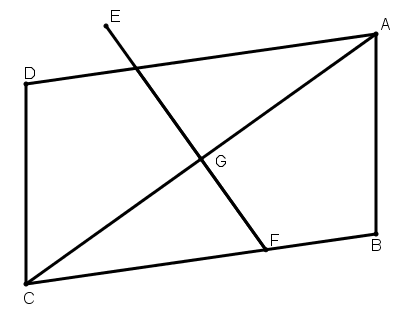
[96 – сурет].

 

[XVI] Егер ол АВСD параллелограмынан, мысалы оның сыртында жатқан Е нүктесінен өтетін сызық арқылы үштен бір, төрттен бір немесе одан да басқа бөліктерін табу керек десе, онда АВСD фигурасын үшке бөлеміз, алдыңғыдай АВ сызығына параллель GH cызығын жүргіземіз. Е нүктесі арқылы GHCD фигурасын бөлетін EFI сызығын жүргіземіз. Сонда FIDC трапециясы ABCD фигурасының үштен бір бөлігі. Міне оның суреті [97 – сурет].

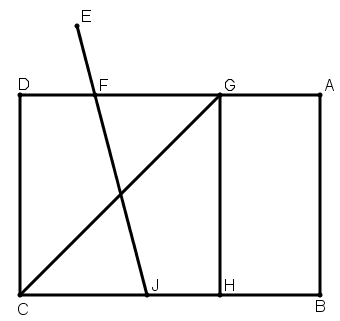
[97 – сурет].

 

[XVII] Егер ол  АВСD  трапециясынан, мысалы  белгіленген нүктеден Е нүктесінен өтетін сызықпен үштен бір, төрттен бір немесе басқа бір бөлігін бөлу керек десе, онда  AD сызығы ВС сызығы параллель, оның үштен бір бөлігі. ВС сызығының үштен бір бөлігі болып табылатын BG сызығын қоя тұрып, Е және G нүктелерін қосамыз. Сонда егер АD–ның АЕ және ВС–ның BG үштен бір бөлігі, онда EG сызығы АВСD трапециясының үштен бір бөлігін бөліп алады⁵¹. Міне оның суреті [98 – сурет]

 

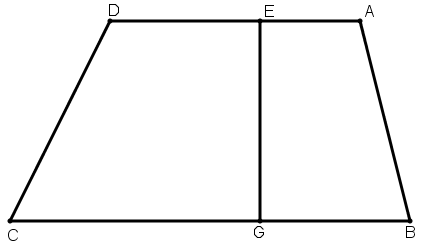
[98 – сурет].

 

[XVIII] Егер АЕ сызығы АD–ның үштен бір бөлігі болмаса, онда АD–ның үштен бір бөлігі болатын AG–ды қоя тұрамыз, және AG AE–ден қысқа болсын. Сол сияқты ВС–ның үштен бір бөлігі ВН–ты қоя тұрып, G және H нүктелерін қосамыз. GH–ты ортасынан  F нүктесімен бөлеміз. EF нүктелерін қосып оны I нүктесімен жалғастырып қосамыз. Онда EFI  сызығы ABCD трапециясын үшке бөледі, бұл – AEIB трапециясы болады. Міне оның суреті [99 – сурет].

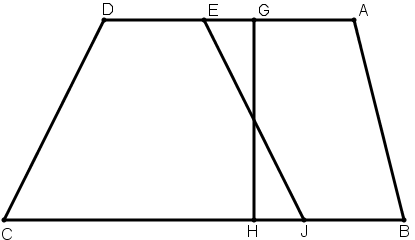
[99 – сурет].

                                                                                        

[XIX] Егер ол АВСD трапециясын, трапецияға тиісті емес, мысалы Е нүктесінен өтетін сызықпен қалай қақ бөледі десе, онда АВ сызығы G нүктесінде қақ бөлеміз, G нүктесі арқылы GD сызығына параллель GF сызығын жүргіземіз және AD сызығын Н нүктесімен қиылысқанша жүргіземіз [GF сызығымен]. HFCD параллелограмы шығады. Е нүктесі арқылы EIK сызығын жүргіземіз, ол HFCD фигурасын қақ бөледі. Онда EIK сызығы АВСD трапециясын қақ бөледі. Міне оның суреті [100 – сурет].

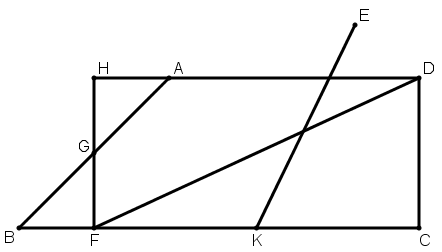
[100 – сурет].

 

[XX] Егер ол ABCD трапециясының қандай да бір бөлігін,  одан тысқары жатқан, мысалы Е нүктесі арқылы өтетін сызықпен қалай бөлуге болады десе, онда АВ–ны G нүктесінде қақ бөлеміз, ол нүкте  арқылы DC–ге параллель HG сызығын сызамыз, Е нүктесі арқылы HFCD параллелограмынан бөліп тұратын  EІK сызығын HFCD параллелограмынан қажетті үлесті бөлетін EJK сызығын сызамыз; сонда ABCD трапециясынан қажетті бөлікті аламыз. Міне оның суреті [101 – сурет].

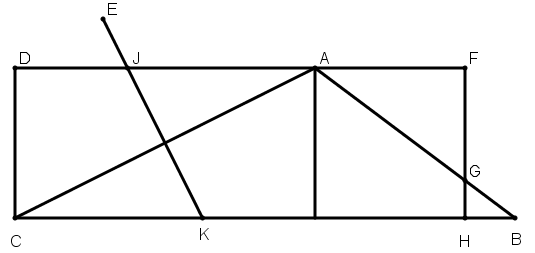
[101 – сурет].

 

[XXI] Егер ол ABCD трапециясының үштен бір бөлігін қалай бөліп алуға болады десе, онда АС мен BD–ні қосамыз. Олар Е нүктесінде қиылыссын. Егер BE сызығы BD–нің үштен бірі болса, онда ABCD фигурасынан үштен бір бөліктің бөлінгені; бұл–ABD үшбұрышы. Міне оның суреті [102 – сурет].

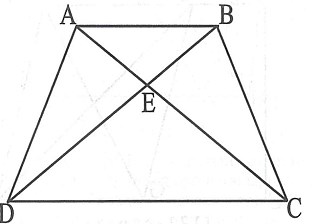
[102 – сурет]

 

[XXII] Егер BE BD–ның үштен біріне тең емес болса, онда CD–ны BD–ның үштен біріне тең болатындай етіп аламыз, G нүктесі арқылы  AC түзуіне паралель GH түзуін жүргіземіз және AH–ты қосамыз. Сонда ABCD фигурасынан үштен бірі бөлініп алынады. Міне оның суреті [103 – сурет].

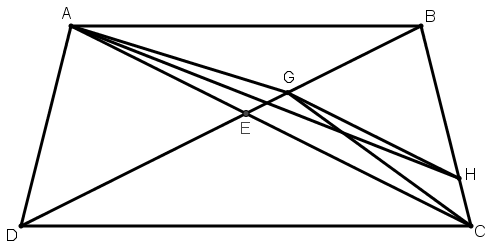
[103 – сурет].

 

[XXIII] Егер ол ABCD фигурасынан оның қабырғасында жатқан нүкте арқылы, мысалы, Е нүктесі арқылы өтетін сызықпен үштен бір бөлігін қалай бөлуге болады десе, онда ABCD пішінінен үштен бір бөлігін бөлетін В нүктесі арқылы BG сызығын сызамыз және EG мен ED сызықтарын сызамыз. Егер EG сызығы BD сызығына параллель, ал DC АЕВ сызығына параллель болса, онда ED сызығымен ABCD фигурасынан үштен бір бөлік бөлінді. Міне оның суреті [104 – сурет].

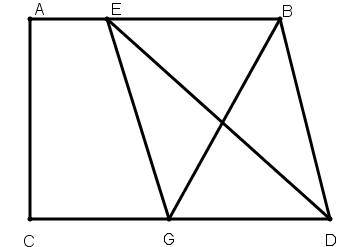
[104 – сурет].

 

[XXIV] Егер BD сызығы EG–га параллель болмаса, онда В нүктесі арқылы фигураның ішінде немесе одан тысқары орналасқан EG сызығына параллель ВН сызығын сызамыз. Алғашында ол сызық фигура ішінде болсын. Е–ні Н–пен қосамыз. Сонда ЕН сызығы ABCD фигурасынан үштен бір бөлігін бөледі. Міне оның суреті [105 – сурет].

 

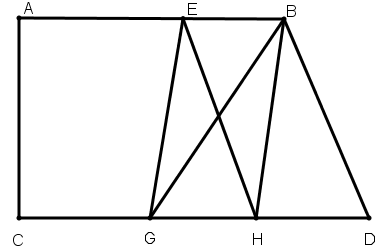
[105 – сурет].

 

[XXV] Егер ВН сызығы фигурадан тысқары орналасқан болса, онда ED–ні қосамыз, CD–ні Н–қа дейін созамыз, DE–ге параллель HF сызамыз және Е–ні Ғ–пен қосамыз. Сонда ЕҒ сызығы ABCD фигурасынан үштен бір бөлік бөледі. Міне оның суреті [106 – сурет].

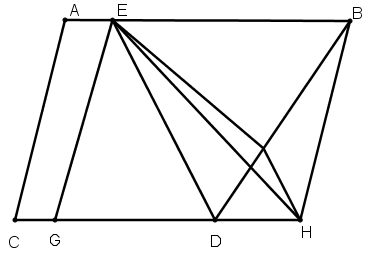
[106 – сурет].

 

[XXVI] Егер ол ABCD шаршысын суретте көрсетілген шаршыға тең болатындай етіп, оның әрбір қабырғасы ұзартылатын болып, қалай үлкейтуге болады – десе, онда DB сызығын өз бағытымен ВЕ–нің, BD–нің екі еселенген ұзындығына тең болатындай етіп Е нүктесіне дейін созамыз. DE сызығының бойына EGD жарты дөңгелегін сырттай сызамыз, АВ сызығын G нүктесіне дейін созып, квадраттың әрбір қабырғасына AG сызығының жартысына тең сызықтар өлшеп салып, шаршыны толықтырамыз; ABCD шаршысы өзіне тең шамаға ұлғаяды⁵². Міне оның суреті [107 – сурет].

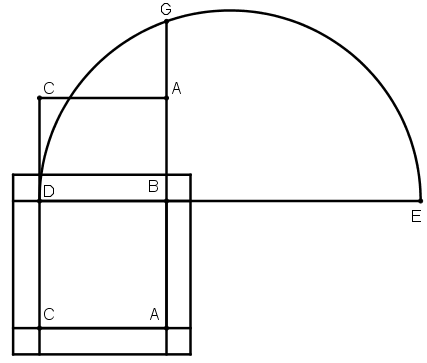
[107 – сурет].

 

Егер біз шаршыны бірнеше есе ұлғайтқымыз келсе, жоғарыдағыдағыдай орындаймыз: бұл жағдайда BE сызығын әлгі еселік санмен бірдей болатын BD сызығына тең етеміз.

[XXVII] Егер ол ABCD шаршысының ортасына суретте көрсетілгендей шаршының жартысына тең болатын шаршыны қалай салу керек десе, онда BD сызығынан мұның жартысына тең болатын BE сызығын өлшеп саламыз. DE сызығының бойына АВ–ні G нүктесінде қиятын DGE жарты дөңгелегін сырттай сызамыз да, AG сызығының жартысына тең ВН сызығын саламыз. А, В, С және D сызығының бұрыштарынан НВ сызығына тең сызықтарды өлшеп саламыз және де бөлу тұстарынан шаршының қабырғаларына параллель сызықтар сызамыз. Сонда ABCD шаршысының ортасында FJLK шаршысы пайда болады, бұл ABCD–ның жартысына тең болады. Міне оның суреті [108 – сурет].

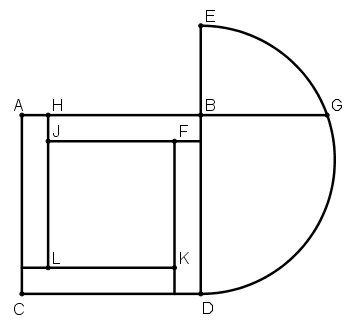
[108 – сурет].

 

[XXVIII] Егер ол ABC дөңгелегінің үштен бір немесе төрттен бір немесе басқа бөліктерін  параллель екі сызықпен қалай бөлуге болады десе, онда D нүктесін дөңгелектің центрі деп, дөңгелектің ішіне оның үштен бір бөлігіне тең болатын хорда сызамыз, бұл – АС сызығы болады, АС–ге параллель BD–ні сызамыз және В мен С–ні қосамыз. AC доғасын Е нүктесінде қақ бөлеміз де, Е нүктесі арқылы ВС–ге параллель EG сызығын сызамыз. Сонда дөңгелектің ішіндегі параллель екі сызық арасында орналасқан GBCE пішіні дөңгелектің үштен бір бөлігі болып табылады. Міне оның суреті [109 – сурет].

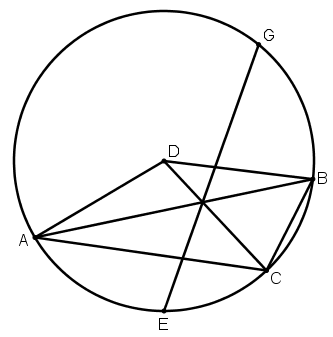
[109 – сурет].

 

[XXIX] Егер ол ABC секторын қалай қақ бөлуге болады десе, онда ВС доғасын D нүктесінде қақ бөлеміз де, А мен D–ні қосамыз, сонда, егер СА сызығы АВ–ға тең болса, онда ABC пішіні AD сызығымен қақ бөлінетін болады. Егер де АС сызығы АВ–ге тең болмаса, онда СВ сызығын Е нүктесінде қақ бөлеміз, AD сызығына параллель EG–ді сызамыз және де D мен G–ді қосамыз. Сонда ABCD пішіні DG сызығымен қақ бөлінетін болады. Міне оның суреті [110 – сурет].

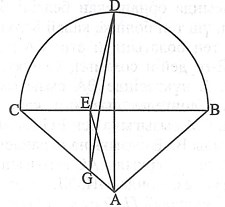
[110 – сурет].

 

[XXX] Із қалдыру туралы. Егер ол ABCD шаршысын ені DH–ке тең із қалдырып қалай қақ бөлуге болады десе, онда СА– ны бағыты бойынша МА сызығын СН–қа тең болатындай етіп М–ге дейін созамыз, ВА–ны оның бағыты бойынша L–ге дейін созамыз, дөңгелектің С ортасынан СМ аралығында ВА сызығын L нүктесінде қиятын сырттай дөңгелек сызамыз да, L–ді С–мен қосамыз. СН–қа тең LK–ны өлшеп саламыз, AL сызығына параллель KEG сызығын сызамыз және DB сызығына параллель HF–ті сызамыз. Сонда НЕ фигурасы ЕВ фигурасына тең болады⁵³. Міне оның суреті [111 – сурет].

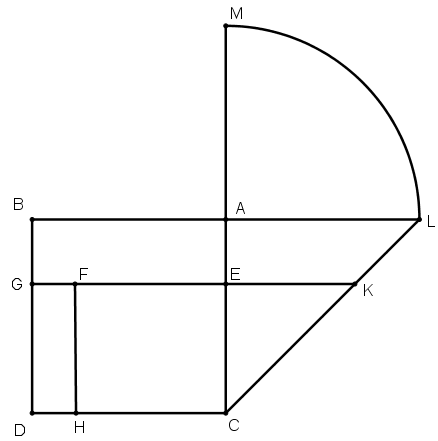
[111 – сурет].

 

[XXXI] Егер ол ABCD шаршысын CD қабырғасында екі тең кесінді арасында орналасқан белгілі бір ені MN болатын із қалдырылып, үш тең бөлікке қалай бөлуге болады десе, онда AJ сызығы СМ–ге тең болатындай етіп СА–ны J–ге дейін, ВА–ны бағыты бойынша Е–ге дейін созамыз, С нүктесін дөңгелектің центрі ретінде алып, Е нүктесінде ВА сызығымен қиылысатын CJ аралығында сырттай дөңгелек сызамыз және СЕ–ні қосамыз. СЕ сызығының бойына СМ сызығына тең EG сызығын өлшеп саламыз және G нүктесі арқылы ВАЕ сызығына параллель GHL сызығын сызамыз. М және N нүктелері арқылы АС сызығына параллель MF және NK сызықтарын сызамыз. Сонда МН, NL және AL пішіндері тең болады. Міне оның суреті [112 – сурет].

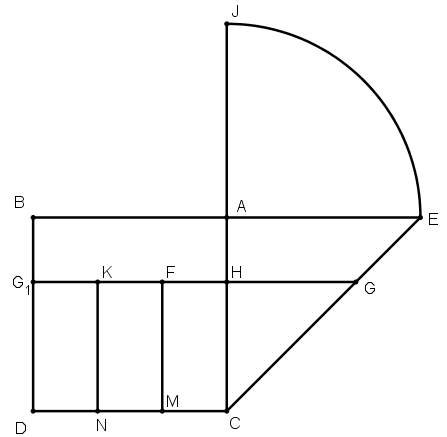
[112 – сурет].

 

[XXXII] Егер ол: АВС үшбұрышын белгілі енімен із қалдыра отырып және егер із ені – CD болса тең екі бөлікке бөлуге болады десе: онда CD –ны Е нүктесінде қақ бөлеміз, ВС–ға параллель EG мен DH–ты жүргіземіз, АС–ға параллель HF–ті жүргіземіз, G мен  F–ті қосамыз, НG –ға тең НК–ны аламыз,  GF–ге параллель KL–ді жүргіземіз, AL трапециясының жартысына тең келетін және АВС үшбұрышы сияқты NMG үшбұрышын тұрғызамыз. MN–ді О–ға дейін жалғастырамыз. Сонда АВС үшбұрышы екі бірдей бөлікке бөлінеді: ВМО үшбұрышы  және АХ трапециясы, олардың арасында ені CD–ге тең ХС із қалған. Міне оның суреті [113 – сурет].

 

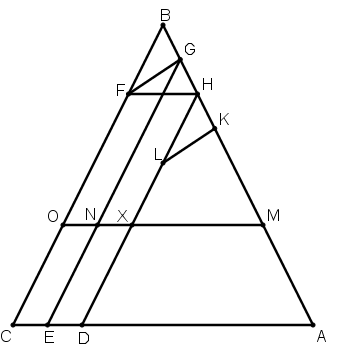
[113 – сурет].

 

[ХХХШ] Егер ол: ені ED–ге тең із қалдырылып, ABC үшбұрышын үштен бір, үштен екі бөлікке қалай бөлуге болады десе, онда CD–нің үштен бір бөлігіне тең СЕ–ні өлшеп саламыз, ВС сызығына параллель DH және EG–ні сызамыз, Н нүктесі арқылы АС сызығына параллель HF сызығын саламыз, СҒ–ті қосамыз және HG–ге тең НК–ні өлшеп саламыз. Одан кейін GF–ке параллель KL–ді сызамыз, AL трапециясының үштен бір бөлігіне тең және ABC үшбұрышына ұқсас GMN үшбұрышын саламыз және MN–ді О–ға дейін созамыз. Сонда ABC үшбұрышы үштен бір бөлікке және үштен екі бөлікке тең, сонымен қатар үштен бір бөлік ВМО үшбұрышына, ал үштен екі бөлігі АХ трапециясына тең. Міне оның суреті [114 – сурет].

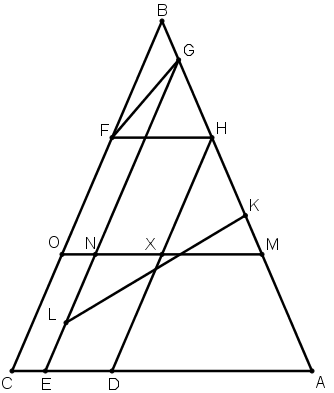
[114 – сурет].

 

[XXXIV] Егер ол: ABCD трапециясын ені ED–ге тең із қалдырып,  BC AD сызығына параллель болғанда қалай қақ бөлуге болады десе,  онда G нүктесінде DE–ні қақ бөлеміз, CD сызығына паралель GH және EF түзуін жүргіземіз, AB және GH сызықтарын M нүктесінде қиылысқанша созамыз және AF трапециясының жартысына тең және MAG үшбұрышы сияқты MLK үшбұрышын тұрғызамыз.  AD сызығына параллель KXLN жүргіземіз. NXED  ізі қалған теңдей екі XKAE және  NCBK трапециялары шығады. Міне оның суреті [115 – сурет].

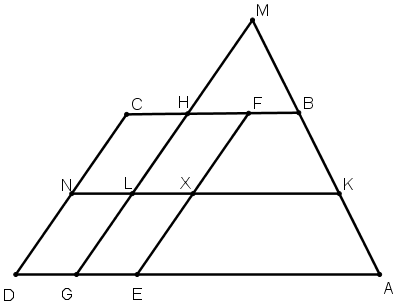
[115 – сурет].