мұралары
мұралары
арифметикалық негіздері

XI тарау. Бір градустык, хорданы анықтау туралы жәнеоларкылы басқа хордаларды құрастыру
Жетінші тарауда шеңбердің алтыдан бір және оннан бір, яғни шеңбердің он екіден бір бөлігіндей хордалардың айырымын, ал сегізінші тарауда жарты және жартының жартысын т.с.с. жарты градустық доғаның хордасына дейін және жарты градустық доғаның хордасынан ширек градустық доғаның хордасына дейін қалай анықтауға болатыны түсіндірілген болатын.
Осыларға сүйене отырып, ABC шеңберін алайық және төрт градустан бастап АВ сызығы алғашында жарты доғаның хордасы, ал АС сызығы - бір градус (32-сурет) доғаның хордасы болсын. Сонда АС хордасының АВ хордасына қатынасы АС доғаның АВ доғаға қатынасынан кіші; АС доғасы АВ доғасының үштен біріне тең. Сондықтан АС хордасы АВ хордасынан үштен бірге кіші. АВ хордасының үштен бірі – 1p2`49``52```.
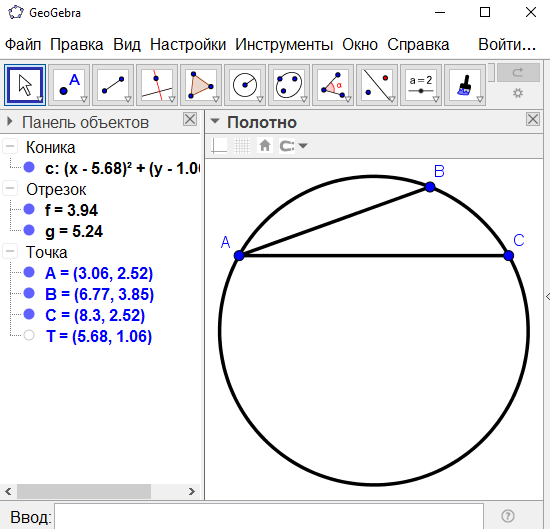
Сурет 32-Бір градустық хорданы анықтау
Дәл осылай осы шеңберде бір градустық доға - АВ сызығын және жарты градустық - АС сызығын сызамыз, сонда АС доғасы жарты доға АВ-ге теңжәне АС хордасы АВ жарты хордасынан кіші болады. Сол себепті АВ доғасы АС доғасының үштен екісінен үлкен, үштен екі доға 1 р 2' 49" 48"'.
Егер бір градустық бір хорда бір кезде кіші, ал басқа кезде заттардан үлкен болса, бұлардың айырымы аз болса, осы айырымды қақ бөліп кішісіне қосамыз. Сонда бір градустық хорда жуықтап алғанда 1р2'49"55"", ал оның толықтырушы хордасы 119°59'43"43"' табылады. Осыдан бір градустың синусы 1р2'49"43"", ал бір градустың косинусы 59Р59'27"7"".
Тоғызыншы тарауда екі доғаның хордаларының қосындысы түсіндірілген болатын, сондықтан, егер бір градустық хорда белгілі болса, онда екі градустық доға да белгілі болады; дәл осы сияқты егер бір және екі градустық хордалар белгілі болса, онда үш градустық хорда да белгілі болады; осылай егер бір және үш градустық хордалар белгілі болса, онда төрт градустық хорда да белгілі болады. Осылайша бір градустық доғаның хордасынан бастап жүз сексен градустық доғаның хордасын құрамыз. Егер синус анықталатын болса, онда тоқсан градусқа градустық доғаның хордасы анықталады. Біз бұларды кесте түрінде орналастырамыз. Міне, 6іздің дәлелдегіміз келгені.




.png)