IV тарау. Шеңбердің хордасының үштен бір бөлігінің шамасын анықтау туралы

АВС- шеңбер болсын, оның диаметрі - АС. Жартыдиаметрге тең ВС-ны жүргізейік; бұл шеңбердің алтыдан бірінің хордасы (25-сурет). АВ-ны жүргізейік. Мен АВ- шеңбердің үштен бірінің хордасы және ол белгілі деп тұжырымдаймын.

Осының дәлелдеуі. АВС бұрышы - тік, себебі ол жартылай шеңберге іштей сызылған, сондықтан АС-ның квадраты АВ мен ВС-ның квадраттарына тең; АС-ның квадраты белгілі, шеңбердің алтыдан бірінің хордасы болып табылатын ВС-ның квадраты да белгілі, сондықтан АС-ның квадратының қалдығы болып табылатын АВ-ның квадраты белгілі; осыдан оның түбірі де, яғни АВ хордасы белгілі. Бұл біздің дәлелдегіміз келгені.

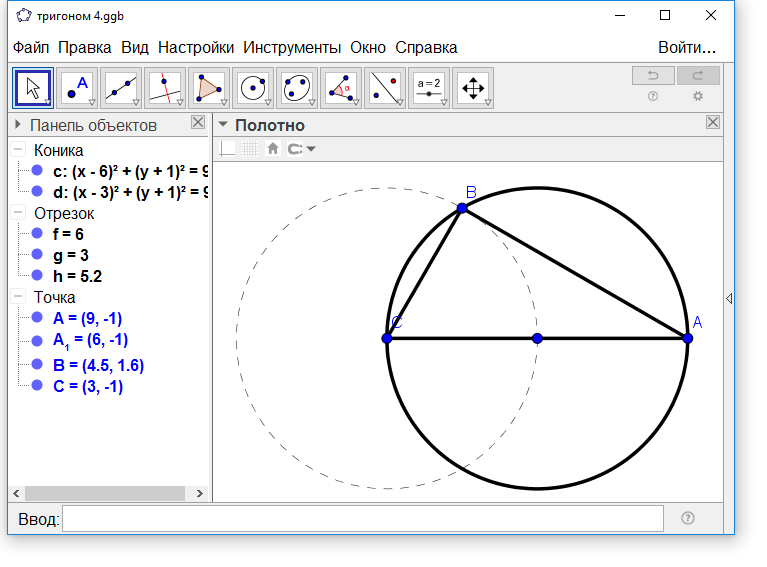
Сурет 25-Шеңбердің хордасының үштен бір бөлігі

Осыдан, шеңбер үштен бірінің хордасының квадраты жартыдиаметрдің үш квадратына тең, себебі диаметрдің квадраты жартыдиаметрдің төрт квадратына тең, ал ВС хордасы жартыдиаметрге тең; егер АС-дан ВС-ның квадратын алатын болсақ, онда АВ хордасының квадратына тең үш еселенген жартыдиаметрдің квадраты қалады.