мұралары
мұралары
арифметикалық негіздері

III тарау. Шеңбердің ширек хордасының шамаларын анықтау туралы
АВС- шеңбер болсын, Е- оның центрі, АС- диаметрі. ЕВ-ны тік бұрышпен жүргіземіз (24-сурет). А-мен В-ны, В-мен С-ны қосамыз. АВ және ВС доғаларының әрбірі шеңбер ширегіне тең, сондықтан АВ, ВС сызықтарының әрбірі ширек шеңбердің хордасы болады. Мен олар белгілі деп тұжырымдаймын.
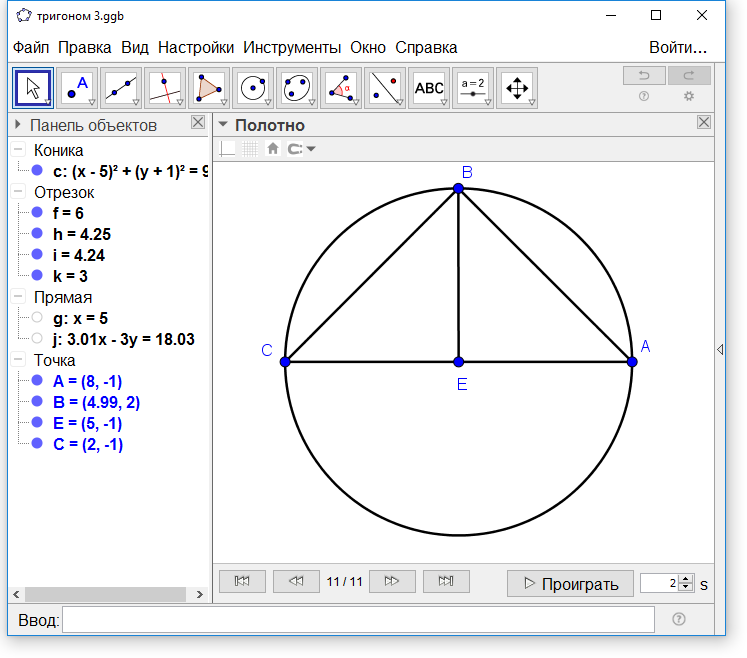
Сурет 24-Ширек хордасының шамаларын анықтау
Осының дәлелдеуі. АЕВ бұрышы тік болғандықтан, АВ-ның квадраты АЕ мен ЕВ-ның квадраттарына тең; бірақ АЕ мен ЕВ [сызықтарының] әрбірі - жартыдиаметр, сондықтан олардың квадраттарының суммасы белгілі, және осыдан, оның түбірі, яғни АВ хордасы белгілі. Бұл біздің дәлелдегіміз келгені.
Осыдан шеңбер ширегінің хордасының квадраты жартыдиаметрдің екі квадратына тең екендігі айқындалады. Диаметрдің квадраты жартыдиаметрдің төрт квадратына тең, себебі
АС-ның квадраты АВ мен ВС-ның квадраттарына тең және АВ мен ВС квадраттардың әрбірі АЕ-ның екі квадратына тең, сондықтан АС-ның квадраты АЕ-ның төрт квадратына тең. Бұл да сол суреттен белгілі.




.png)