Сфераларды бөлу туралы

[I] Егер ол сферада үлкен дөңгелекті қалай жүргізуге болады десе,  онда осында кез– келген С полюсті АВG дөңгелегін саламыз, ары қарай АВG дөңгелегін   А және В нүктелерінде қақ бөлеміз де  А,С,В және D нүктелері арқылы өтетін сферада дөңгелек саламыз. Бұл сферадағы үлкен дөңгелек  болады.  Міне оның суреті [137 – сурет].

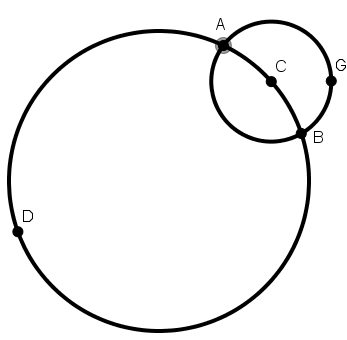
[137 – сурет].

 

[II] Егер ол сферада тік бұрышпен қиылысатын екі үлкен дөңгелекті қалай жүргізуге болады десе,  онда сферада үлкен дөңгелек жүргіземіз, мысалы ABCD дөңгелегі, және оны A,B,C,D нүктелері арқылы тең төрт бөлікке бөлеміз. Ары қарай А нүктесін полюс ретінде қабылдап,  [А–дан] B және D ара қашықтығында  дөңгелек саламыз. Бұл BED  дөңгелегі болады. ABCD және  BED екі үлкен дөңгелек тік бұрыш арқылы қиылысады. Міне оның суреті [138 – сурет].

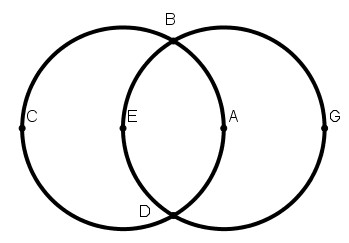
[138 – сурет].

 

[III] Егер ол сферада тік бұрышпен қиылысатын үш үлкен дөңгелек жүргіземіз десе, онда бұрынғыдай А және С нүктелерінде тік бұрышпен қиылысатын екі үлкен дөңгелек саламыз. Бұл тік бұрышпен қиылысатын ABCD және  BEDG дөңгелектері. Ары қарай   BCD доғасын С нүктесінде қақ бөлеміз, В нүктесін полюс етіп алып ВС қашықтықта СЕAG  дөңгелегін саламыз. Сонда бір бірімен тік бұрышпен⁵⁹  қиылысатын  ABCD, BEDG және CEAG үш дөңгелегін аламыз. Міне оның суреті [139 – сурет].

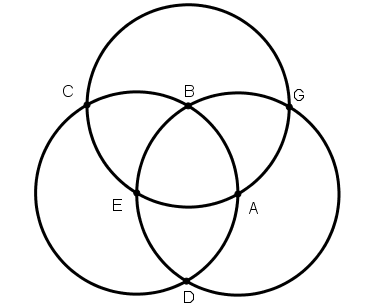
[139 – сурет].

 

  [IV] Егер ол сфераның екі нүктесі арқылы өтетін үлкен   дөңгелекті  қалай жүргізуге болады десе, онда осы нүктелердің әрбірін [бұл А және В нүктелері болсын]  полюс ретінде қабылдап үлкен дөңгелектің төрттен біріндей қашықтықта CDEB және CGEA дөңгелектерін саламыз.   Бұл дөңгелектер  С және Е нүктелерінде қиылысады. Әрі қарай бұл дөңгелектердің қиылысу орнын полюс ретінде қабылдаймыз және {осыдан} {берілген} нүктеге дейінгі қашықтықта дөңгелек тұрғызамыз, бұл үлкен дөңгелек болып саналатын АВН болсын. Міне оның суреті [140 – сурет].

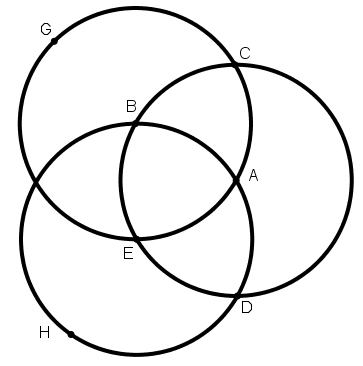
[140 – сурет].

 

[V] Тең қабырғалы үшбұрыш болатындай  сфераны теңдей төрт бөлікке бөлу туралы. Егер ол тең қабырғалы және тең бүйірлі үшбұрыш болатындай  сфераны қалай теңдей төрт бөлікке бөлу керек десе, онда үш дөңгелек жүргіземіз: бұл дөңгелектер ABCD, BEDG  және CEAG. Сонда сфераны теңдей сегіз үшбұрышқа бөлеміз; бұл үшбұрыштар ABE, AED, ADG, AGB, CBE, CED, CDG және CGB. Үшбұрыштардың біреуінің центрі және осы үшбұрыштың әр бұрышы арқылы үлкен дөңгелектер доғаларын жүргіземіз және оларды тиіп тұрған үшбұрыштардың центріне дейін жалғастырамыз. Егер біз әрбір үшбұрыш үшін осы центрден қалған екі бұрышқа дейін доғалар жүргізсек және оларды [тиіп тұрған] үшбұрыштардың центріне дейін жалғастырсақ, онда біз тең қабырғалы және тең бүйірлі үшбұрыш болатындай  сфераны теңдей төрт бөлікке бөлеміз: бұл үшбұрыштар IHF, IKH және FKH және  FIK⁶⁰.  Міне оның суреті [141 – сурет].

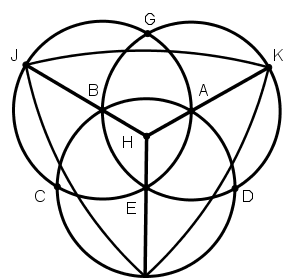
[141 – сурет].

 

  [VІ] Тең қабырғалы және тең бұрышты үшбұрыш болатындай  сфераны теңдей төрт бөлікке бөлудің басқа [тәсілі]. Егер ол тең қабырғалы және тең бұрышты теңдей үш үшбұрыш болатындай  сфераны қалай теңдей төрт бөлікке бөлу керек десе, егер сфераның диаметрі белгілі болса, онда егер сфераның диаметрі AB сызығына тең болса, AB сызығында жарты дөңгелек тұрғызамыз да AB–ның үштен біріне тең  AB–ны белгілейміз,  AB–ға перпендикульяр  CD  сызығын жүргіземіз. Ол жарты дөңгелекпен D нүктесінде қилысады. дөңгелектен кез– келген Е нүктесін белгілеп, оны полюс  ретінде қабылдап BD–қашықтықта FGH дөңгелегін сызамыз да,  G, H, F нүктелерінде теңдей үш бөлікке бөлеміз және полюс пен G, H, F нүктелерінің әрқайсысы арқылы I нүктесінде қиылысатын  үлкен дөңгелектің доғаларын, ал  әрбір екі G, H және F нүктелері арқылы үлкен дөңгелек доғаларын  жүргіземіз. Сонда тең қабырғалы және тең бүйірлі үшбұрыш болатындай  теңдей төрт бөлікке бөлінген сфера аламыз. Бұл IHF, IHG, FIG және GHF⁶¹үшбұрыштары.  Міне оның суреті [142 – сурет].

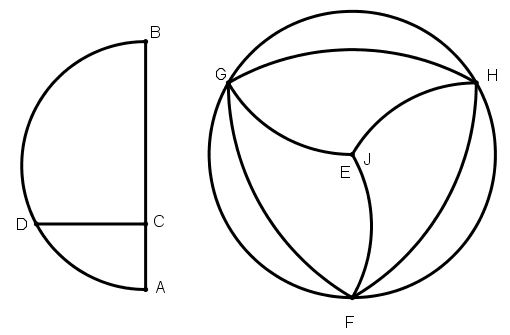
[142 – сурет].

 

  [VІІ] Тең қабырғалы және тең бұрышты төртбұрыш болатындай  сфераны теңдей алты бөлікке бөлу туралы. Егер біз осыны тұрғызғымыз келсе, онда тік бұрышпен қиылысатын үш үлкен дөңгелек тұрғызамыз. Ары қарай сферада өзіміз алған сегіз үшбұрыштың әрбір екеуінің ценрті арқылы үлкен дөңгелектер доғасын жүргіземіз. Сонда сфера тең қабырғалы және тең бүйірлі төртбұрыш болатындай  теңдей алты бөлікке бөлінеді және не салғымыз келсе, соны аламыз⁶². Міне оның суреті [143 – сурет].

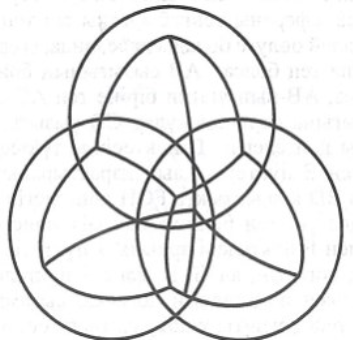
[143 – сурет].

 

  [VIII] Сфераны тең қабырғалы және тең бұрышты алты төртбұрышқа бөлудің келесі бір әдісі. Егер ол сфераны қалай тең қабырғалы және тең бұрышты алты төртбұрышқа бөлуге болады десе, егер сфераның диаметрі АВ кесіндісіне тең болса, онда АВ кесіндісі бойынан жарты дөңгелек сызамыз, АВ–ның үштен біріне тең болатын АС–ны белгілейміз, С нүктесінен АС ға перпендикуляр СD–ны тұрғызып, А мен D нүктелерін қосамыз, сфераға Е және G нүктелерінде тік бұрышпен қиылысатын екі дөңгелекті саламыз, әрбір Е және G нүктелерін полюс ретінде қабылдап АD қашықтықта H, F, I, К, L, Μ, Ν және X нүктелерін белгілейміз, осы нүктелердің әрқайсысынан үлкен дөңгелек жүргіземіз, яғни төрт доға H, F, I және К нүктелерінің және L, Μ, Ν, X нүктелерінен арасынан жүргіземіз.

Сонда сфера алты тең қабырғалы және тең бұрышты төртбұрышқа бөлінеді⁶³. Міне оның суреті [144 – сурет].

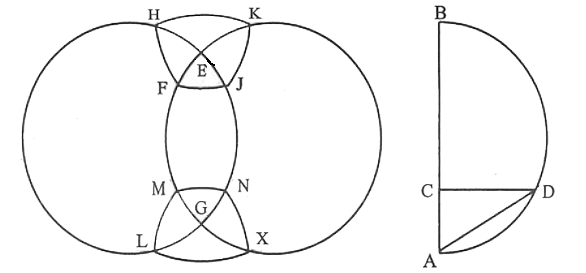
[144 – сурет].

 

  [ІХ] Тең қабырғалы және тең бұрышты үшбұрыш болатындай  сфераны теңдей жиырма бөлікке бөлу туралы. Егер ол тең қабырғалы және тең бұрышты үшбұрыш болатындай сфераны қалай теңдей жиырма бөлікке бөлуге болады десе, онда полюсы H және G нүктелері болатын сферада үлкен ABCD дөңгелегін тұрғызамыз. Бұл дөңгелекті теңдей он бөлікке бөлеміз; Бұл бөліктер AB, BC, CD, DE, EF, FI, IK, KL, LM  және MA. A және B нүктелерін полюс терінде қабылдап, BC доғасы қашықтығында Н жағында Z нүктесінде қиылысатын екі дөңгелек сызамыз. Содан соң B және C нүктелерін полюс терінде қабылдап, BC доғасы қашықтығында Q жағында G нүктесінде қиылысатын екі дөңгелек сызамыз. Үлкен дөңгелектің он бөлігінің әрбірінде, он бөлікке бөлінген,   Н жағында Z нүктесінде және G жағында Q нүктесінде қиылысатын дөңгелектер сызамыз. Бізде Z–пен белгіленетін Н полюсі жағынан бес нүкте және Q–мен белгіленетін Н полюсі жағынан бес нүкте пайда болады. Осы нүктелердің әрбір екеуін, яғни Z және Q–ді үлкен дөңгелектің доғаларымен қосамыз. Төбелері Z және Q болатын, ал табандары  QQ және ZZ сызықтары болатын он үшбұрыш пайда болады. Ары қарай әрбір Z нүктесі мен H полюсі және әрбір Q нүктесі мен G полюсі арқылы үлкен дөңгелек доғаларын жүргіземіз. Төбелері H нүктесінде болатын бес үшбұрыш және төбелері G нүктесінде болатын бес үшбұрыш пайда болады. Осындай әдіспен сфераны теңдей тең қабырғалы және тең бұрышты жиырма үшбұрышқа бөлеміз⁶⁴. Міне оның суреті [145 – сурет].

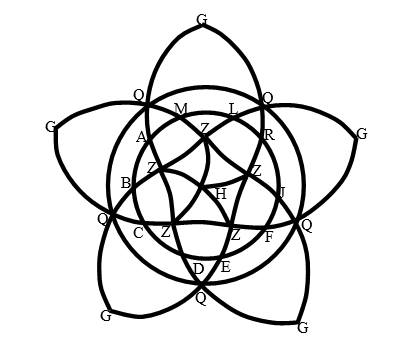
[145 – сурет].

 

  [Х] Осы салудың басқа әдісі. Егер біз тең қабырғалы және тең бұрышты үшбұрыш болатындай  сфераны теңдей жиырма бөлікке бөлгіміз келсе және сфераның диаметрі AB сызығына тең болса, онда AB сызығының бойында ABC жарты дөңгелегін тұрғызамыз, AB–ның бестен біріне тең BD–ны белгілейміз, DB сызығына перпендикуляр DC тұрғызамыз,  B нүктесін центр ретінде қабылдаймыз және BC қашықтықта CEG дөңгелегін саламыз. CEG дөңгелегінің бестен біріне тең CE доғасын белгілейміз. Сферада кез–келген H нүктесін белгілеп, оны полюс ретінде қабылдаймыз және CE қашықтықта сферада дөңгелек тұрғызамыз. Дөңгелекті F нүктесінде теңдей бес бөлікке бөлеміз, әрбір екі осындай нүктелер арқылы үлкен дөңгелек доғаларын жүргіземіз және  әрбір осы нүктелер мен полюс арқылы дәл сондай үлкен дөңгелек доғаларын жүргіземіз. Сферада төбелері H нүктесінде және табандары FF болатын тең қабырғалы және тең бұрышты бес үшбұрыш аламыз. Ары қарай F нүктесінің әрбірін полюс ретінде аламыз және I нүктесінде қиылысатын, алынған қашықтықта дөңгелектер тұрғызамыз.  Содан соң әрбір екі F нүктесі және әрбір екі I нүктесі арқылы үлкен дөңгелек доғаларын жүргіземіз. Сонда тең қабырғалы және тең бұрышты он үшбұрыш аламыз. Содан соң әрбір екі I нүктесін полюс ретінде аламыз және сондай қашықтықта K нүктесінде қиылысатын дөңгелектер сызамыз. Содан соң әрбір I нүктесіне және әрбір K нүктесіне үлкен дөңгелек доғаларын тұрғызамыз. Сонда тең қабырғалы және тең бұрышты бес үшбұрыш аламыз. Сәйкесінше, сфераның жоғарғы бетін тең қабырғалы және тең бұрышты үшбұрыш болатындай жиырма бөлікке бөлеміз⁶⁵.  Міне оның суреті [146 – сурет].

 

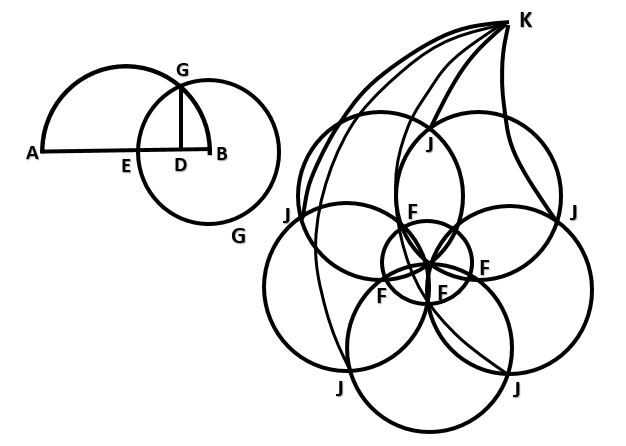
[146 – сурет].

 

Бұл кітапты бітірудің кезі келді. Мұхаммед пен оның ұрпағы үшін дұға және екі дүниенің билеушісі Аллаға шексіз алғыс! Осы жұмыс ғалым Мухаммед Әбу Насыр ибн  Мухаммед  ибн Узлағ ибн Тархан әл Фәрәбидің қолымен үш жүз жиырма бірінші жылы он бірінші раджабта аяқталды.  Біздерге ақыл сыйлаушының даңқы шексіз арта берсін!