мұралары
мұралары
арифметикалық негіздері

ӘОЖ 37:514:004.738.1 (574)
Рахимжанов Е.Е., Жаксылыков А.Е., Умбетбаев К.У.
О РАЗРАБОТКЕ ЭЛЕКТРОННЫХ ПОСОБИЙ ПО ГЕОМЕТРИЧЕСКИМ НАСЛЕДИЯМ АЛЬ-ФАРАБИ И ОБРАЗОВАТЕЛЬНОГО ПОРТАЛА
Казахский национальный педагогический университет имени Абая, Казахстан, Алматы
В статье представлены общие видения по созданию образовательного портала по математическому наследию аль-Фараби. Проанализированы ведущие образовательные ресурсы, их структура для улушения функциональности образовательного портала. Приведены технологии и платформы, используемые для создания портала. А также приведен пример построения анимации на языке javaScript как обучающий элемент.
Ключевые слова: аль-Фараби, образовательный портал, электронные средства обучения
Мақалада әл-Фарабидің математикалық мұрасы бойынша білім беру порталын жасаудың жалпы көріністері ұсынылған. Жетекші білім беру ресурстары, олардың құрылымына талдау жасалған. Портал жасау үшін қолданылатын технологиялар мен платформалар берілген.
Кілттік создер: әл-Фараби, білім беру порталы, электрондық оқыту құралдары
Common views of creating educational portal on mathematical heritage of al-Farabi are given in the article. Leading educational resourses, their structure are analyzed. Technologies and platforms used for creating the portal are given.
Keywords: al-Farabi, educational portal, e-learning tools
Цели создания портала
Используя достижения информационных технологий показать пути эффективного использования математических наследий аль-Фараби в современном математическом образовании. Разработать учебно-методическое пособие, электронные средства обучения с помощью информационно-коммуникационных технологий, предназначенные для обучения геометрическим построениям по алгоритмам, предлагаемым в математическом трактате аль-Фараби [1].
Создавая портал по математическим наследиям аль-Фараби, нелишним было бы взглянуть на опыт других разработчиков для улушения функциональности образовательного портала. Интересен опыт, в первую очередь, ведущих образовательных ресурсов [2]. Все эти ресурсы можно условно поделить на 2 категории:
1) предоставляющие доступ к многочисленным материалам (текст, видео и пр.) на различные темы;
2) сайты, ориентированные на одну тематику.
В качестве примера к 1-ой категории можно отнести следующие ресурсы:
- Coursera (www.coursera.org) - бесплатные курсы Стэнфордского Университета.
- Edx (www.edx.org) - онлайн-курсы Гарвардского Университета. Онлайн-курсы и лекции от одного из престижнейших вузов. Среди разработчиков ПО широко получила известность благодаря фундаментальным курсам по программированию.
Если проанализировать структуру этих сайтов, то можно отметить следующее:
- Контент этих сайтов выложен в виде лекций в текстовой форме или в виде видео;
- Так как количество тем затрагиваемых на таких сайтах велико, имеется поиск по ключевым словам, деление на категории. Также имеется система рейтингов (оценивание) курсов для того чтобы из множества доступных курсов выводить пользователям по порядку наиболее популярные из них.
- Нередко встречаются на подобных сайтах системы проверки знаний.
В качестве примера ко 2-ой категории можно отнести следующие ресурсы:
- https://developer.mozilla.org/ru - предоставляет информацию об открытых веб-технологиях
- http://learn.javascript.ru - обучающий ресурс по javaScript
В отличии от вышеперечисленных ресурсов, преподнесение информации больше ориентирована на одну конкретную тематику. Навигация и структура подобных сайтов рассчитана на хорошее усвоение материала одной темы. В отличии от вышеперечисленных ресурсов, где располагаются образовательные материалы различных тематик, в данном случае сайт полностью адаптируется под одну тему, используя все имеющиеся ресурсы, предоставляемые платформой, на которой функционирует портал. В частности, в случае нашего портала «Математическое наследие Аль-Фараби», используется технологии HTML svg, canvas для визуализации геометрических построений, для интерактивного взаимодействия с пользователями сайта.
Проанализируем в качестве примера learn.javascript.ru.
В данном ресурсе, посвященному изучению языка javaScript, учебный материал разбит на основной и дополнительный, навигация осуществляется с помощью левой фиксированной панели и дополнительных стрелок. Примеры уроков возможно запускать в браузере пользователей (так как это javaScript), благодаря чему экономится время пользователей на запуск программ примеров. Для каждого урока имеется возможность оставлять пользователям комментарии.
Для портала аль-Фараби на наш взгляд оптимальным будет создание сайта, включающего функционал сайтов как первой, так и второй категории.
Исходя из анализа вышеприведенных нами были определены примерная структура образовательного портала по математическим наследиям аль-Фараби.
Структура портала
В разработке структура портала (рис.1), состоящая из трех частей как одно целое, но отличающиеся технологией построения, дизайном на двух языках – казахском и русском и частично на английском:
- Биография Аль Фараби, труды исследователей о наследиях Аль Фараби т.д. Другие материалы образовательно-исследовательского характера. (Восточный (арабский) оттенок дизайна свойственный Казахстану начинается с этого раздела и, по возможности, присутствует везде );
- Материалы, связанные с мультимедийными представлениями математических объектов и ходом доказательств, а также методиками и технологиями обучения и т.д. Это - основная часть образовательного портала, отражающая нашу текущую научно-исследовательскую работу в основном. На наш взглад, с точки зрения графического оформления максимально простое, но наиболее функциональное;
- Блоги, форумы т.д. Возможно, они интегрируются с вышеперечисленным разделом как одно целое. Или отдельно с обучениями.
Дизайн портала – адаптивный, рассчитанный в первую очередь на мобильные устройства.
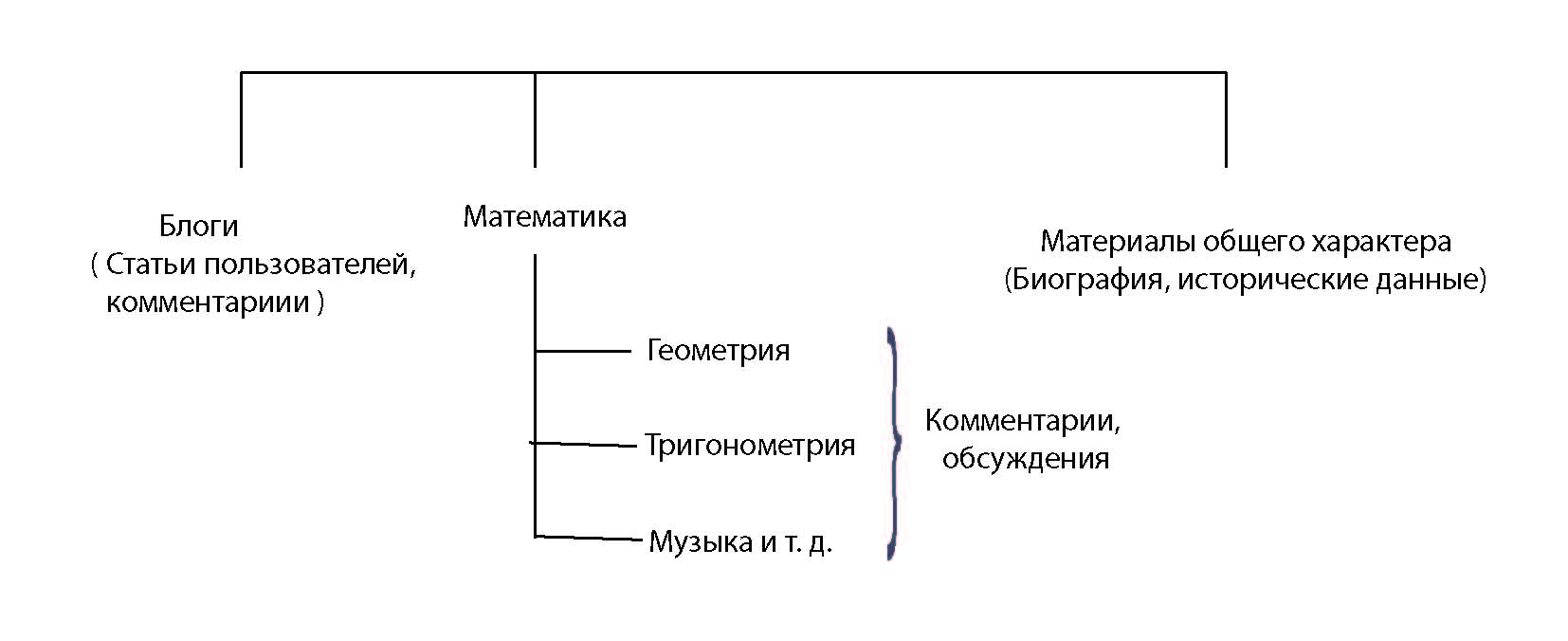
Рисунок 1. Примерная структура образовательного портала.
Нами создается портал, в котором содержаться мультимедийные, обучающие материалы, блоги, комментарии, статьи в тесной взаимосвязи друг с другом как единое целое а не как набор разрозненных модулей, материалов, связанных с наследиями выдающимся нашим предком аль-Фараби. Для этого мы начали с создания библиотеки для программирования анимаций геометрических построений. По мере его усовершенствования в планах создание библиотеки, который позволял бы пользователям рисовать на сцене геометрические фигуры, вводить формулы и т.д. В последующем это позволит использовать ее для вставки геометрических фигур и формул в комментариях, обсуждениях а также использовать как основной модуль в простых компьютерных играх. В планах реализация возможности масштабирования сцены, в котором будут использоваться своя независимая система координат, возможность перемещения по этой сцене движением мыши или пальцев. Это позволит создавать на сцене геометрические фигуры, которые будут хорошо отображаться на устройствах с разным разрешения экрана (смартфоны, планшеты). В качестве примера можно привести программу GeoGebra (рис. 2).
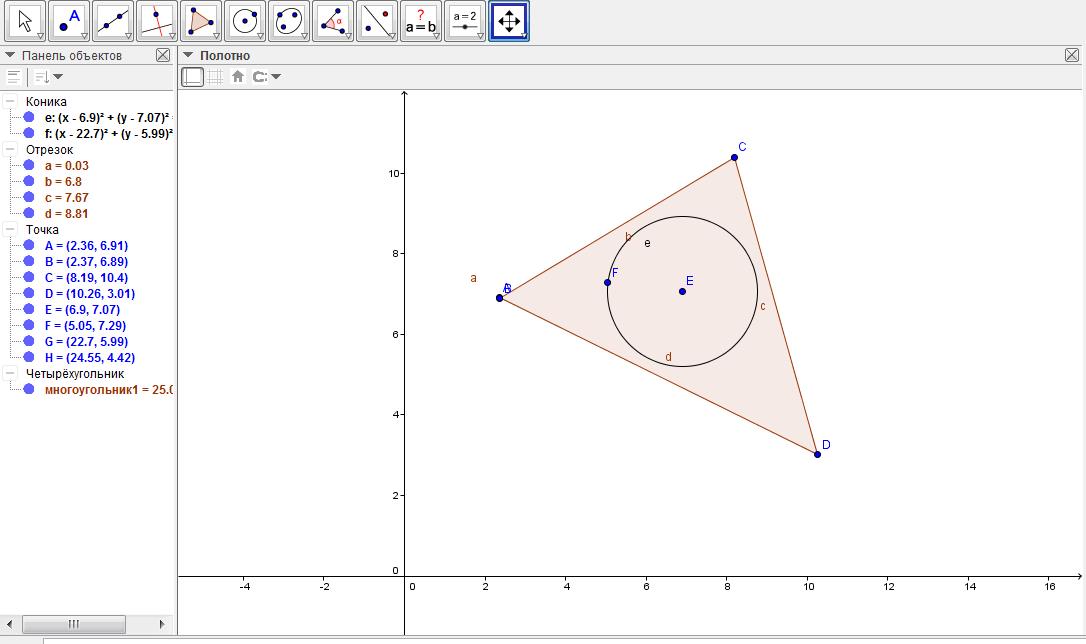
Рисунок 2. Скриншот экрана GeoGebra. В GeoGebra используется своя система координат и возможность перемещения, масштабирования сцены.
Помимо возможности вставлять формулы и геометрические фигуры пользователями сайта в планах реализация функции поиска по формулам по всему порталу.
Реализация этих и других возможностей позволит более гибче подходить к построению функциональной части образовательного портала по математическим наследиям аль-Фараби.
Для реализации подобной функциональности образовательного портала нами были выбраны соответствующие платформы и технологии.
Платформы и технологии:
В качестве веб платформы используется PHP YII2 Framework. На клиентской стороне для отображения анимаций используется HTML5: svg, canvas и JavaScript. Выбор в пользу HTML5 пал не случайно, так как HTML5 поддерживается практически всеми современными платформами (linux, Windows, Apple iOS, Android и пр.), и это дает возможность отображать весь сайт на мобильных устройствах не урезая функционал.
Пример анимации геометрических построений с использованием библиотеки на javaScript и svg.
var stage = new MAAF.Stage(); // объект сцены
var f1 = function(){
MAAF.pointB=stage.point();
MAAF.pointB.setCoord({coord: {x: 450, y: 300}, label: 'B'});
MAAF.pointA=stage.point();
MAAF.pointA.setCoord({coord: {x: 250, y: 300}, label: 'A'});
MAAF.pointA.draw();
return MAAF.pointB.draw();
}
var f2 = function(){
MAAF.lineAB = stage.line();
MAAF.lineAB.setPoints({p1:MAAF.pointA,p2:MAAF.pointB});
return MAAF.lineAB.draw();
};
var f4 = function(){
return stage.divider.changeSolution({p1:MAAF.pointA, p2:MAAF.pointB});
};
var f5 = function(){
MAAF.cr1 = stage.circle();
MAAF.cr1.setCenter(MAAF.pointB);
MAAF.cr1.setRadius(stage.divider.solution);
return MAAF.cr1.draw();
};
Вот рисунок этого (рис, 3).
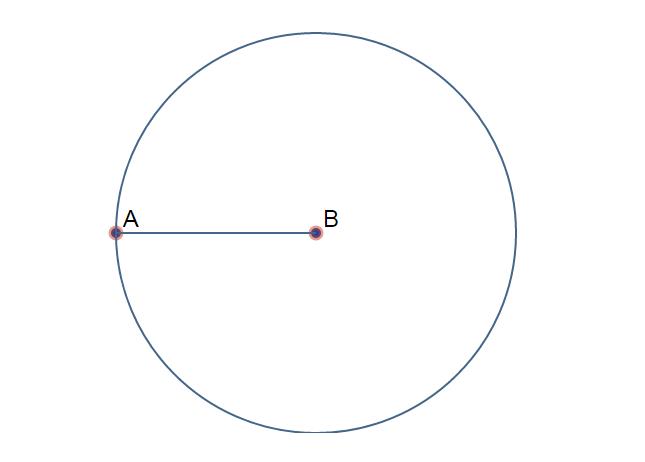
Рисунок 3. Построение круга, испльзуя библиотеку.
Некоторые полученные результаты по поставленным целям данного проекта были апробированы и обсуждены в нескольких международных конференциях и получили положительные отзывы слушателей.
Эти полученные результаты были изложены в Институте математики Академии наук РК, были обсуждены во 2-ом Международном Аль-Фараби форуме в виде электронного образовательного ресурса (рис 4.) [3].
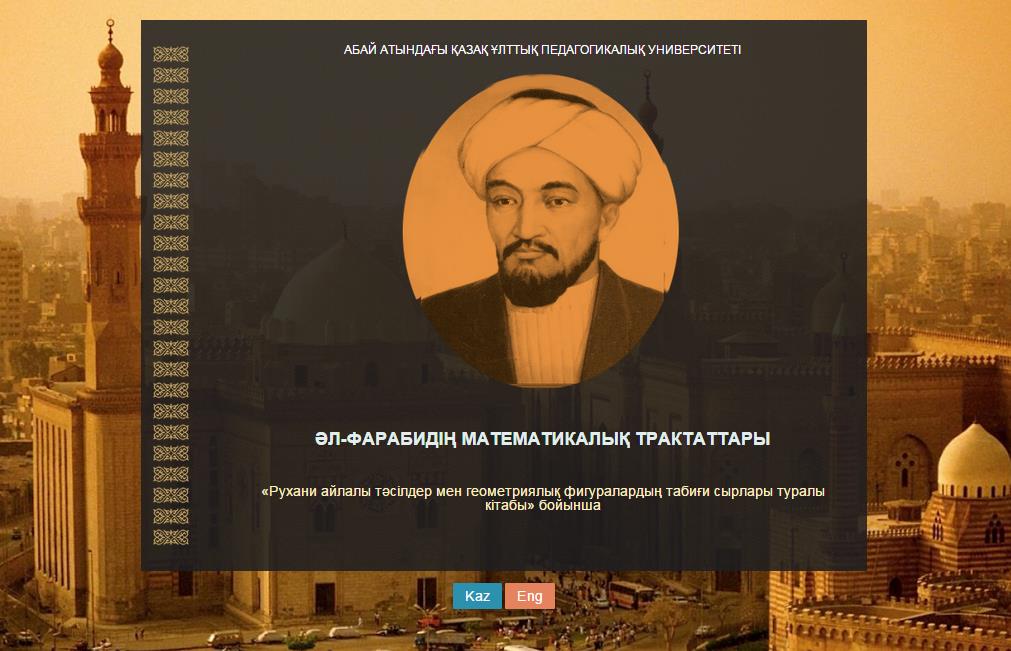
Рисунок 4. Электронное средство обучения по геометрическим построениям аль-Фараби
Список литературы
1. Аль-Фараби, Математические трактаты. – Алма-Ата, 1972.
2. http://habrahabr.ru/company/mailru/blog/235165/
3. Бидайбеков Е.Ы., Камалова Г.Б., Бостанов Б.Ғ., Джанабердиева С.А. Әл-Фарабидің математикалық мұралары заманауи білім беру аясында // ВЕСТНИК КазНУ, Серия философия. Серия культурология. Серия политология, №2/1 (51),Алматы, «Қазақ университеті», 2015, С 443-447.




.png)