Кейбір фигураларға іштей басқа фигураларды салу туралы

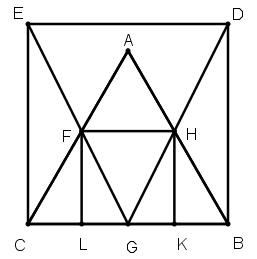
[I] Теңқабырғалы төртбұрышқа іштей үшбұрыш салу туралы. Егер ол теңқабырғалы төртбұрышқа іштей теңқабырғалы үшбұрышты қалай салу керек десе, онда ABCD шаршысын тұрғызамыз, DC сызығын Е нүктесіне дейін созамыз және CE–ні CD–ға тең қыламыз. ED сызығына жарты дөңгелек тұрғызамыз, D нүктесін центр ретінде алып DC қашықтықта G нүктесін белгілейміз. Ары қарай E нүктесін центр ретінде қабылдаймыз және EG қашықтықта H нүктесін белгілеп, DH–қа тең AF тұрғызып, B–мен F–ті, B–мен H–ты, F–пен H–ты қосамыз. ABCD шаршысына іштей  сызылған BFH теңқабырғалы үшбұрышын аламыз. Міне оның суреті [49 – сурет].

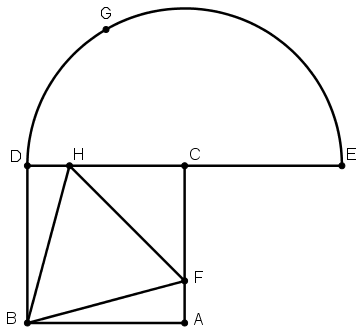
[49 – сурет].

 

[IІ] Теңқабырғалы төртбұрышқа іштей үшбұрыш салудың екінші әдісі. Егер қаласақ, BD сызығында  BDE теңқабырғалы үшбұрышын тұрғызамыз, EBD бұрышын BG сызығымен қақ бөлеміз, AF сызығын  DH сызығына тең қыламыз, BH, BF және FH сызықтарын жүргіземіз, ABCD шаршысына іштей  сызылған теңқабырғалы және теңбұрышты BFH үшбұрышын аламыз. Міне оның суреті [50 – сурет].

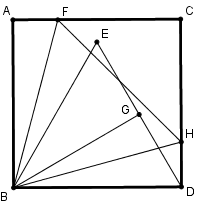
[50 – сурет].

 

[IІІ] Теңқабырғалы төртбұрышқа іштей үшбұрыш салудың үшінші әдісі. Егер қаласақ, әрбір AD және BC сызықтарын E және G нүктелерінде қақ бөлеміз, EG –ні қосамыз,  A нүктесін центр ретінде аламыз және AB қашықтықта BH доғасын сызамыз. Екі еселенген GH сызығына тең  CF және AI сызықтарын саламыз. BI, BF және FI сызықтарын жүргіземіз; ABCD шаршысына іштей  сызылған теңқабырғалы BFI үшбұрышы пайда болады. Міне оның суреті [51 – сурет].

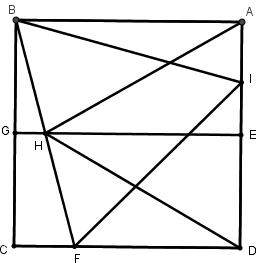
[51 – сурет].

 

[IV] Теңқабырғалы төртбұрышқа іштей үшбұрыш салудың төртінші әдісі. Шаршы салып, әрбір AD және BC сызықтарын E және H нүктелерінде қақ бөлеміз, EH–ты қосамыз,  B нүктесін центр ретінде аламыз және BC қашықтықта G нүктесін белгілейміз, EH сызығын GF сызығы GH сызығына тең болатындай, оның бағытында F нүктесіне дейін созамыз,  BF–ті қосамыз, ол AD сызығын K нүктесінде қияды. AK–ға тең CI–ді салып, BK, BI және IK сызықтарын жүргіземіз.  ABCD шаршысына іштей  сызылған теңқабырғалы BKI үшбұрышын аламыз. Міне оның суреті [52 – сурет].

[52 – сурет].

 

[V] Теңқабырғалы төртбұрышқа іштей үшбұрыш салудың бесінші әдісі. Егер біз осыны салғымыз келсе, ABCD шаршысына сырттай дөңгелек сызамыз, оның центрі Е, BD диаметрін сызамыз, D нүктесін центр ретінде аламыз және DE қашықтықта H және G нүктелерін белгілейміз, BG және BH сызықтарын, F және I нүктелерінде қиылысатын  AD және DC сызықтарын жүргіземіз және FI–ді қосамыз.  ABCD шаршысына іштей  сызылған теңқабырғалы BFI үшбұрышын аламыз. Міне оның суреті [53 – сурет].

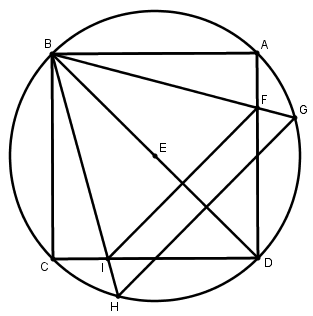
[53 – сурет].

 

[VI] Шаршыға сырттай сызылған үшбұрыш салу туралы. Егер ол ABCD шаршысына сырттай теңқабырғалы үшбұрышты қалай салу керек десе, онда AB сызығына теңқабырғалы  ABE үшбұрышын тұрғызамыз, EA, EB сызықтарын олардың бағытында созамыз, сондай-ақ    CD сызығын EA, EB сызықтарының жалғасымен G және H нүктелерінде қиылысқанға дейін созамыз. Сонда ABCD шаршысына сырттай  сызылған теңқабырғалы EGH үшбұрышын аламыз. Міне оның суреті [54 – сурет].

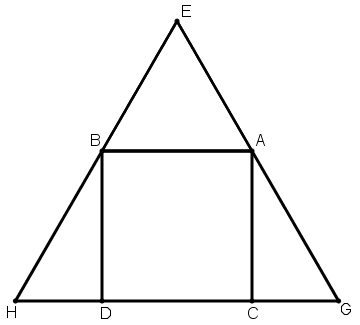
[54 – сурет].

 

[VIІ] Үшбұрышқа сырттай сызылған шаршыны салу туралы. Егер ол теңқабырғалы үшбұрышқа сырттай теңқабырғалы және теңбұрышты төртбұрышты қалай салу керек десе, онда ABC теңқабырғалы  үшбұрышын тұрғызамыз, AC қабырғасын D нүктесінде қақ бөлеміз, BD сызығын E–ге дейін созамыз, DE сызығын AD–ға тең қылып аламыз, E мен A–ны, E мен C–ны қосамыз, EA және EH сызықтарына B нүктесінен BG және BH перпендикулярларын түсіреміз. Теңқабырғалы үшбұрышқа сырттай сызылған BGEH теңқабырғалы және теңбұрышты төртбұрышын аламыз. Міне оның суреті [55 – сурет].

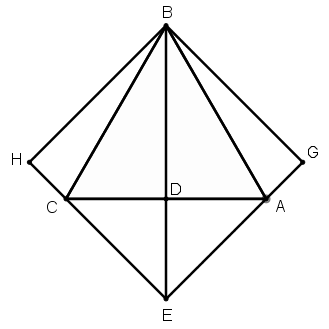
[55 – сурет].

 

[VIІІ] Теңқабырғалы емес үшбұрышқа сырттай шаршы салу туралы. Егер ол қабырғалары әр түрлі ABC үшбұрышына сырттай теңқабырғалы және теңбұрышты төртбұрышты қалай салу керек десе, онда С нүктесінен CA сызығына CD перпендикулярын түсіреміз, оны осы сызыққа тең етіп, D–мен B–ны қосамыз және DB–ны оның бағытында созамыз, CE–ға С нүктесінен CG перпендикулярын жүргіземіз, A нүктесінен CE–ға параллель сызық жүргіземіз, бұл HA сызығы. Қабырғалары әр түрлі ABC үшбұрышына сырттай теңқабырғалы және теңбұрышты HGCE төртбұрышын аламыз. Міне оның суреті [56 – сурет].

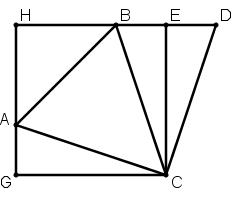
[56 – сурет].

 

[ІX] Үшбұрышқа сырттай сызылған шаршыны салудың екінші тәсілі. Егер ол қабырғалары әр түрлі ABC үшбұрышына сырттай теңқабырғалы және теңбұрышты шаршыны қалай салу керек десе, онда С нүктесінен CA сызығына CD перпендикулярын түсіреміз, оны осы сызыққа тең етіп, D– мен B–ны қосамыз және DB–ны оның бағытында созамыз, CE–ға С нүктесінен CG перпендикулярын жүргіземіз, A нүктесінен CE–ға параллель сызық жүргіземіз, бұл HA сызығы. Қабырғалары әр түрлі ABC үшбұрышына сырттай теңқабырғалы және теңбұрышты HGCE төртбұрышын аламыз. Міне оның суреті [57 – сурет].

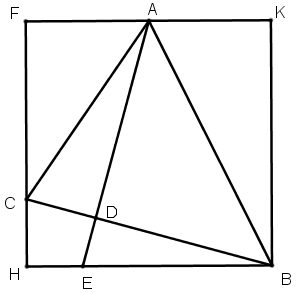
[57 – сурет].

 

[X] Үшбұрышқа сырттай сызылған шаршыны салудың үшінші тәсілі. Егер қаласақ, АВ қабырғасына тең қылып, А нүктесінен АВ сызығына AD перпендикулярын түсіреміз. АВС үшбұрышына тең ADE үшбұрышын тұрғызамыз. Сонда DE  BC–ға тең, ал AE  AC–ға тең. ЕВ қосамыз және С нүктесінен ЕВ сызығында СН перпендикулярын түсіреміз, ал А нүктесінен ЕВ және СН сызықтарында AF және AG перпендикулярларын түсіреміз. Сонда AGHF– шаршы болады. Міне оның суреті [58 – сурет].

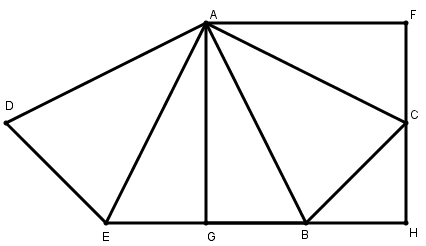
[58 – сурет].

 

[XІ] Үшбұрышқа іштей сызылған шаршыны салу туралы. Егер ол ABC үшбұрышына іштей теңқабырғалы және теңбұрышты шаршыны қалай салу керек десе, онда В нүктесінен ВС сызығына тең BD перпендикулярын тұрғызамыз және AD–мен қосамыз;  AD сызығы BC–мен Е нүктесінде қиылысады. Е нүктесінен ЕВ сызығына EG перпендикулярын тұрғызамыз, ол АВ сызығымен G нүктесінде қиылысады. G нүктесінен ВС сызығына параллель GH сызығын жүргіземіз және  H нүктесінен ВC сызығына HF перпендикулярын түсіреміз. Сонда ABC үшбұрышына іштей сызылған теңқабырғалы және теңбұрышты EGHF төртбұрышы пайда болады. Міне оның суреті [59 – сурет].

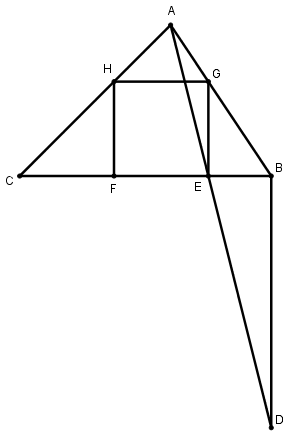
[59 – сурет].

 

[XІІ] Үшбұрышқа іштей сызылған шаршыны салудың екінші әдісі. ВС сызығына тең болатындай В нүктесінен BD перпендикулярын түсіреміз. А нүктесінен АЕ перпендикулярын түсіреміз, D мен Е–ны қосамыз, DE АВ сызығымен G нүктесінде қиылысады;  G нүктесінен ВС сызығына параллель болатын GH сызығын жүргіземіз және ВС сызығына GF және HI перпендикулярларын түсіреміз, сонда ABC үшбұрышына іштей сызылған теңқабырғалы және теңбұрышты GHIF төртбұрышы аламыз. Міне оның суреті [60 – сурет].

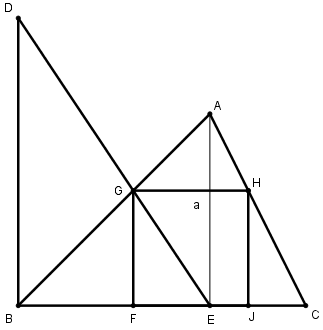
[60 – сурет].

 

[XІІІ] Теңқабырғалы үшбұрышқа іштей сызылған шаршыны салу туралы. Егер қаласақ ВС–да BDEC шаршысын тұрғызамыз,  G нүктесінде ВС сызығын қақ бөлеміз, DG және EG сызықтарын жүргіземіз, олар АВ және АС сызықтарымен H және F нүктелерінде қиылысады, H–ты F–пен қосамыз. Одан HK және FL перпендикулярларын түсіреміз, сонда ABC үшбұрышына іштей сызылған шаршы аламыз. Міне оның суреті [61 және 62–суреттер].

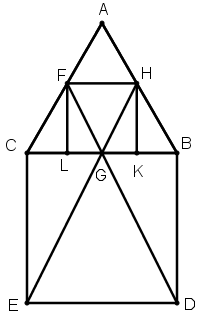
[61 – сурет].

 

[62 – сурет].

 

[XІV] Қабырғалары әр түрлі үшбұрышқа іштей теңқабырғалы үшбұрыш салу туралы. Егер ол бір қабырғасы ВС сызығына параллель қабырғалары әр түрлі АВС үшбұрышына іштей теңқабырғалы үшбұрышты қалай тұрғызамыз десе, онда ВС сызығында BDC теңқабырғалы үшбұрышын тұрғызамыз, AI және DE перпендикулярларын тұрғызамыз, В нүктесінен BC–ға BG перпендикулярын түсіреміз, BH сызығын AI сызығына тең етеміз, ал HG сызығын DE перпендикулярына тең етіп аламыз. С–мен G–ді қосып, H нүктесінен GC сызығына параллель HF сызығын жүргіземіз, сонда BF сызығы бір қабырғасы ВС сызығына параллель және қарсы жатқан бұрыштың төбесі BC–да жататын АВС үшбұрышына іштей сызылған үшбұрыштың қабырғасы. 

Сондықтан егер біз  ABC үшбұрышында BC–ға параллель және BF–ға тең LN сызығын жүргізіп, L нүктесін центр ретінде қабылдаймыз және LN қашықтықта ВС сызығынан М нүктесін белгілесек, онда ABC үшбұрышына  іштей сызылған теңқабырғалы LMN үшбұрышын аламыз. Міне оның суреті [63 – сурет].

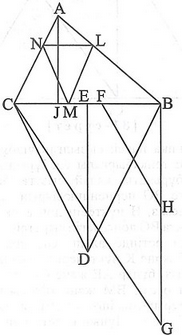
[63 – сурет].

 

[XV] Қабырғалары әр түрлі үшбұрышқа сырттай теңқабырғалы үшбұрыш салу туралы. Егер ол қабырғалары әр түрлі АВС үшбұрышына сырттай теңқабырғалы үшбұрышты қалай саламыз десе, онда ВС сызығына параллель сызық жүргіземіз, ВС сызығында қабырғалары әр түрлі BDC үшбұрышын тұрғызамыз, DB және DC сызықтарын өз бағыттарында созамыз да, А нүктесінен ВС сызығына параллель және DB мен DC сызықтарын E және G нүктелерінде қиятын GAE сызығын жүргіземіз. Сонда теңқабырғалы DEG үшбұрышын аламыз. Міне оның суреті [64 – сурет].

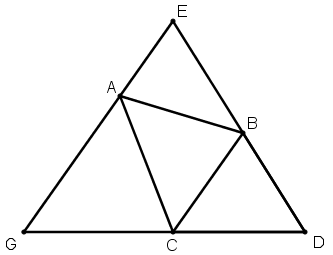
[64 – сурет].

 

[XVI] Бесбұрышқа іштей үшбұрыш салу туралы. Егер ол теңқабырғалы АВСDE бесбұрышына іштей теңқабырғалы үшбұрышты қалай саламыз десе, онда В нүктесінен DE–ге BG перпендикулярын тұрғызамыз, оны H нүктесінде қақ бөлеміз, H нүктесін центр ретінде қабылдап HB қашықтықта BG дөңгелегін сызамыз. G нүктесін центр ретінде қабылдаймыз және GH қашықтықта дөңгелектің бойынан F және K нүктелерін белгілейміз. BK және KF сызықтарын жүргіземіз, олар AE және CD сызықтарын M және N нүктелерінде қияды, BM, BN және MN сызықтарын жүргіземіз. ABCDE бесбұрышына іштей сызылған теңқабырғалы BMN үшбұрышы пайда болады. Міне оның суреті [65 – сурет].

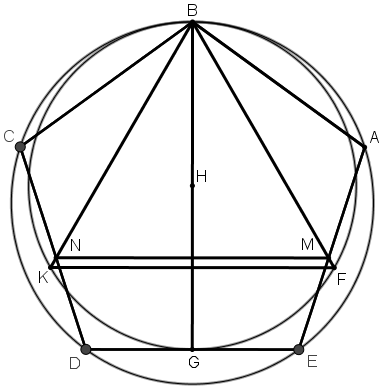
[65 – сурет].

 

[XVIІ] Бесбұрышқа сырттай сызылған үшбұрыш салу туралы. Егер ол теңқабырғалы АВСDE бесбұрышына сырттай теңқабырғалы және теңбұрышты үшбұрышты қалай саламыз десе, онда

Бесбұрышқа іштей теңқабырғалы үшбұрыш саламыз, бұл BGH үшбұрышы, А және С нүктелерінен BG және BH сызықтарына параллель FL және FK екі түзу сызықтарын жүргіземіз, DE сызығын оның екі бағытымен L және K нүктелеріне дейін созамыз. ABCDE бесбұрышына сырттай сызылған теңқабырғалы FLK үшбұрышын алдық. Міне оның суреті [66 – сурет].

[66 – сурет].

 

[XVIIІ] Бесбұрышқа іштей шаршы салу туралы. Егер ол теңқабырғалы және теңбұрышты АВСDE бесбұрышына іштей теңқабырғалы және теңбұрышты төртбұрышты қалай саламыз десе, онда С нүктесінен АЕ сызығына CG перпендикулярын түсіреміз, оны H нүктесінде қақ бөлеміз де, ол арқылы АЕ сызығына параллель FHK сызығын жүргіземіз және C мен F, C мен K,  K мен G, G мен F нүктелерін сызықтармен қосамыз. ABCDE бесбұрышына іштей сызылған теңқабырғалы және теңбұрышты CFGK төртбұрышын аламыз. Міне оның суреті [67 – сурет].

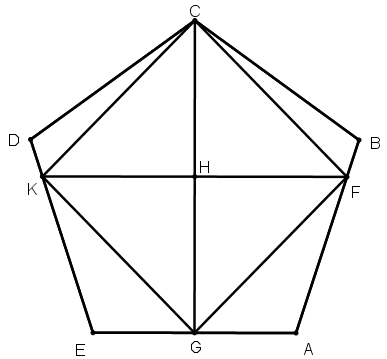
[67 – сурет].

 

[XІX] Бесбұрышқа сырттай шаршы салу туралы. Егер ол теңқабырғалы АВСDE бесбұрышына сырттай теңқабырғалы және теңбұрышты төртбұрышты қалай саламыз десе, онда АЕ сызығын G нүктесінде қақ бөлеміз де, СЕ сызығына тең болатындай GH перпендикулярын тұрғызамыз, H пен E–ні, H–пен A–ны қосамыз да, өз бағыттарында жалғастырып сызамыз, B және D нүктелерінен HF және HL сызықтарына BF және DL перпендикулярларын түсіреміз де, оларды K нүктесіне дейін өз бағыттарында созамыз, сонда ABCDE бесбұрышына сырттай сызылған теңқабырғалы және теңбұрышты FKLH төртбұрышын аламыз. Міне оның суреті [68 – сурет].

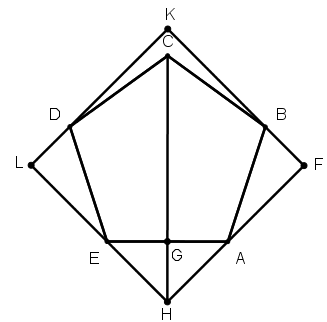
[68 – сурет].

 

[XX] Шаршыға іштей сызылған бесбұрыш салу туралы. Егер ол АВСD шаршысының диагоналында іштей E бұрышты қалаған шамадағы EGHFI бесбұрышына ұқсас теңқабырғалы және теңбұрышты бесбұрышты қалай саламыз десе, онда қалаған шамадағы KLMNX теңқабырғалы бесбұрышын тұрғызамыз және оның маңайына шаршы тұрғызамыз. Оның қабырғаларының бірі– ZQ болсын. ZO сызығын жүргіземіз, AB қабырғасына тең болатындай QP аламыз, P нүктесінен ZO сызығына параллель PG сызығын жүргіземіз, ал R нүктесінен MN қабырғасының  ортасы мен Q нүктесі арқылы өтетін сызық жүргіземіз. АС қосамыз, QR сызығына тең CS белгілейміз, АС сызығына перпендикуляр HSF түруін жүргіземіз. Содан соң H және F нүктелерін центр етіп алып HF қашықтықта AB және AD сызықтарының бойынан G және I нүктелерін белгілейміз. G және I нүктелерін центр етіп алып GH қашықтықта E нүктесін белгілейміз де, HG, GE, EI және IE сызықтарын жүргізіп ABCD шаршысына іштей сызылған EGHFI теңқабырғалы және тең бұрышты бесбұрышын аламыз⁴⁸. Міне оның суреті [69 – сурет].

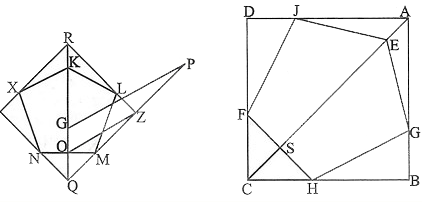
[69 – сурет].

 

[XXI] Шаршыға іштей сызылған сегізбұрыш салу туралы. Егер ол теңқабырғалы және теңбұрышты сегізбұрышты қалай саламыз десе, онда ABCD  шаршысын тұрғызамыз, Е нүктесінде қиылысатын диаметрлерін жүргіземіз, Е нүктесін центр етіп алып, шаршының қабырғасының жартысына тең қашықтықта G нүктесін белгілейміз,  G нүктесін центр ретінде алып, D және G нүктелері қашықтығында H пен F нүктелерін белгілейміз, шаршының қабырғаларының әрбір бұрышынан DF және DH–қа тең сызықтар белгілейміз. Бұл MA, AL, BN, BX, CK, CI сызықтары. HF, IK, LM және NX сызықтарын қосамыз. IKLMNXHF теңқабырғалы және теңбұрышты сегіз бұрышты пайда болды. Міне оның суреті [70 – сурет].

[70 – сурет].

 

[XXIІ] Шаршыға іштей сызылған сегізбұрыш салудың басқа әдісі. Егер қаласақ циркульдің ашасымен шаршы диагоналінің жартысындай яғни AE қашықтықта шаршының әрбір бұрышынан M, N, X, H, F, I, K және L нүктелерін белгілейміз де, LM, NX, HF және IK сызықтарын жүргіземіз.  Теңқабырғалы және теңбұрышты LMNXHFIK сегізбұрышты пайда болады. Міне оның суреті [71 – сурет].

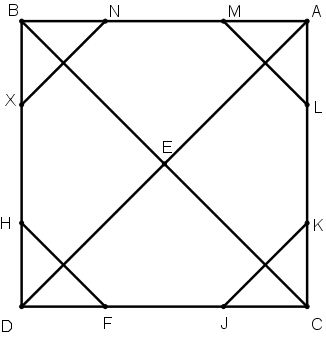
[71 – сурет].

 

[XXIІІ] Сегізбұрышқа сырттай сызылған шаршы салу туралы. Егер ол теңқабырғалы ABCDEGHF сегізбұрышына сырттай шаршыны қалай саламыз десе, онда AB, CD, EG, HF сызықтарын I, K, L, M нүктелерінде қиылысқанша созамыз. Сонда ABCDEGHF сегізбұрышына сырттай сызылған теңқабырғалы және теңбұрышты IKLM төртбұрышын аламыз. Міне оның суреті [72 – сурет].

 

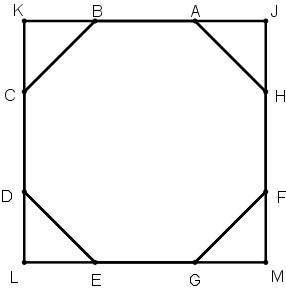
[72 – сурет].