Original text

 Rationale for training

 Visualization

[I] Егер ол сегментті толық дөңгелекке дейін қалай толықтыру керек десе, онда AВС сегментін саламыз да, В нүктесінде қақ бөлеміз. AВ және ВС сызықтарын жүргізіп, AВ мен ВС сызықтарындағы А және С нүктелерінің әрқайсысына ВСD және BAD  тік бұрышынтарын тұрғызамыз. ВD сызығын жүргізіп, оны Е нүктесінде қақ бөлеміз. Сонда E нүктесі ABC⁷ доғасының центрі болып табылады. Міне оның суреті [2 – сурет].

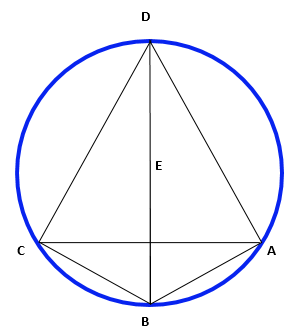
[2 – сурет].

[II] Егер ол центрі D нүктесі болатын ВС дөңгелегіне А нүктесінен қалай жанама жүргізуге болады десе, онда AD сызығын жүргіземіз. Ол ВС дөңгелегін В нүктесінде қияды. D центрінен DА қашықтықта AE дөңгелегін салайық. В нүктесінде АВЕ тік бұрышын тұрғызып, ВС дөңгелегін С нүктесінде қиятын ЕD сызығын жүргіземіз. А – мен С – ны қосамыз. Сонда АС ВС⁸ дөңгелегіне жүргізілген жанама болып табылады. Міне оның суреті [3 – сурет].

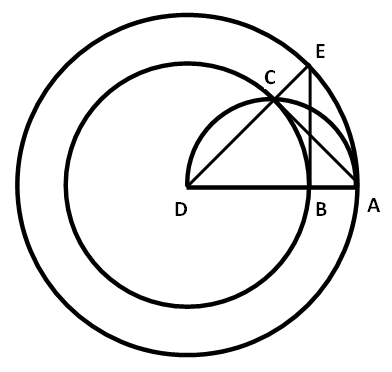
[3 – сурет].

[IIІ] Егер ол жанаманы қолөнершінің тәсілі бойынша сал десе, онда сызғышты ВС сызығына орналастырып циркульді бір шамаға ашамыз; Егер оның бір ұшы сызғыш бойымен қозғалатын болса, онда екінші ұшы А нүктесі арқылы өтіп, ВС⁹–ға параллель сызықты береді. Міне оның суреті [4 – сурет].

 

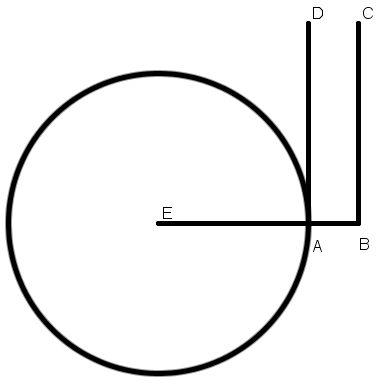
[4 – сурет].

 

[IV] Егер ол: А нүктесінен ABC дөңгелегінің шеңберіне жанаманы қалай жүргізеді десе, онда А нүктесін дөңгелектің центрі D нүктесімен қосамыз, демек А мен D–ны [AD сызығымен] қосамыз. А нүктесінде AD сызығының бойымен DAE тікбұрышын тұрғызамыз. Сонда АЕ сызығы – ABC дөңгелегіне жанама болады¹⁰. Міне оның суреті [5 – сурет].

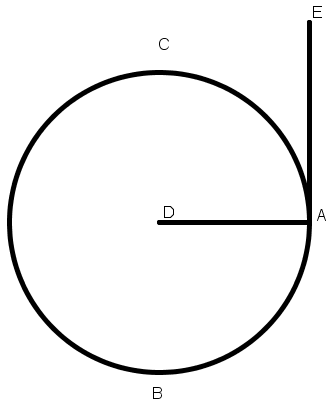
[5 – сурет].

[V] Егер ол АВС үшбұрышының АВ және АС сызықтарының арасына ВС–ға параллель болатын және егер ВС сызығы D сызығынан кіші болған жағдайда берілген D сызығына тең сызық сал десе, онда ВС сызығын оның бағытында [ВЕ D–ға тең болатындай Е нүктесіне дейін] созып, ал [егер ВС D сызығынан үлкен болса] D–ға тең ВЕ сызығын ВС сызығына саламыз. Е нүктесінен АВ сызығына параллель сызық жүргіземіз. Ол АС–ны G нүктесінде қиып өтеді. G нүктесінен ВС сызығына параллель сызық жүргіземіз; Бұл АВ–мен қиылысатын GH сызығы. Сонда GH D сызығана тең және ВС¹¹ сызығына параллель.  Міне оның суреті [6 – сурет].

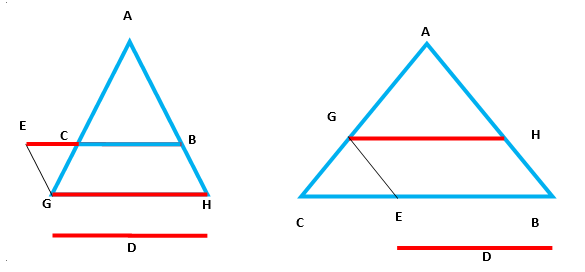
[6 – сурет].

 

[VI] Егер ол АВС үшбұрышының АВ және АС сызықтарының арасына ВС сызығына параллель, мысалы АВ сызығында ол қиып алатын кесіндіге тең, яғни ЕВ сызығына тең DE сызығын салу керек болса, онда АСВ бұрышын BD сызығымен қақ бөлеміз де D нүктесінен ВС–ға параллель DE сызығын жүргіземіз. Сонда DE сызығы ЕВ¹² сызығына тең. Міне оның суреті [7 – сурет].

[7 – сурет].

 

[VII] Егер ол АВС үшбұрышында, мысалы, ВС сызығына параллель және ВЕ мен F сызықтарына тең DE сызығын сал десе, онда ВС сызығына  F сызығына тең BG сызығын салып, G нүктесі арқылы АВ–ға параллель GH сызығын жүргізіп, HGC бұрышын қақ бөлетін GD сызығын [G нүктесі арқылы] жүргіземіз де D нүктесінен ВС сызығына параллель DE сызығын жүргіземіз. Сонда DE сызығы  ВЕ және F¹³ сызықтарына тең. Міне оның суреті [8 – сурет].

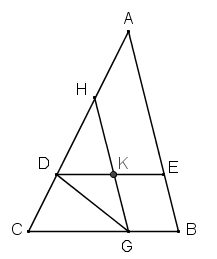
[8 – сурет].

 

[VIII] Басқа үшбұрышқа тең үшбұрышты салу туралы.  Егер ол қабырғалары басқа үшбұрыштың қабырғалырына тең үшбұрышты сал десе [мысалы АВС], онда DE түзу сызығын жүргіземіз де, АВ сызығына тең DG,  BC сызығына тең GH және СА тең HF сызығын  саламыз. G нүктесін центр ретінде қабылдап GD қашықтығында дөңгелек бөлігін келтірейік, сол сияқты H нүктесін центр ретінде қабылдап HF қашықтығында дөңгелек бөлігін келтіреміз. Бірінші бөлігі [екінші бөлігін] I нүктесінде қиып өтеді. Ары қарай GI және ІH сызықтарын жүргізейік. Онда GIH үшбұрышының қабырғалары АВС¹⁴ үшбұрышының қабырғаларына тең. Міне оның суреті [9 – сурет].

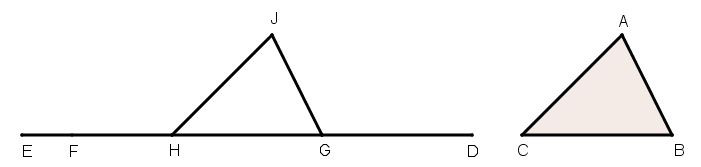
[9 – сурет].

 

[IХ] Бұрышты тең үш бөлікке бөлу туралы. Егер ол АВС бұрышын тең үш бөлікке бөл десе, онда АВС бұрышы тік бұрышты болса, ВС сызығында тең қабырғалы DBC үшбұрышын тұрғызамыз. Сонда ABD бұрышы тік бұрыштың үштен бір бөлігі. DBC бұрышын қақ бөлеміз¹⁵.  Міне оның суреті [10 – сурет].

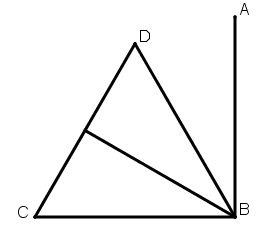
[10 – сурет].

 

[Х] Егер бұрыш тік бұрыштан кіші болса, онда В нүктесін центр ретінде қабылдап ВА қашықтықта DAС дөңгелегін келтіреміз. BD ны ВС–ға тік бұрыш бойынша қойып, СВ–ны дөңгелекпен қиылысқанша Е нүктесіне созамыз. Сызғышты А нүктесіне әкеліп оны CDE дөңгелегінің шеңбері бойынша DB перпендикуляры және DE доғасының арасында жатқан HF сызығы DB сызығына тең болғанша қозғайтын боламыз, бұл жағдайда сызғыш А нүктесінен таймайды. Ары қарай EF доғасына тең EK доғасын саламыз да KB жүргізіп L нүктесіне дейінгі бағытта жалғаймыз. Онда LBC бұрышы АВС бұрышының үштен бірі болады. Әрі қарай ABL бұрышын қақ бөлеміз¹⁶. Міне оның суреті [11 – сурет].

 

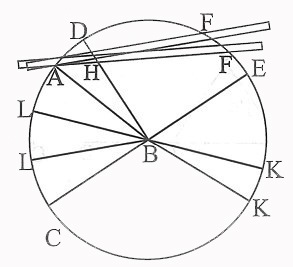
[11 – сурет].

 

[ХІ] Бұрышты тең үшке бөлудің басқа тәсілі.  АВС сүйір бұрышын тұрғызайық та және егер біз оны тең үш бөлікке бөлгіміз келсе, А нүктесінен AH перпендикулярын [ВС сызығына нүктеден түсіреміз]. В нүктесіне сызғышты әкеліп, AD мен AH сызықтарының арасына орналасқан сызық екі еселенген АВ болғанша қозғайтын боламыз. Бұл мысалы DEB сызығы, демек DE сызығы екі еселенген АВ сызығы болып табылады. Ендеше DBC бұрышы АВС¹⁷ бұрышының үштен бір бөлігі. Міне оның суреті [12 – сурет].

.

 

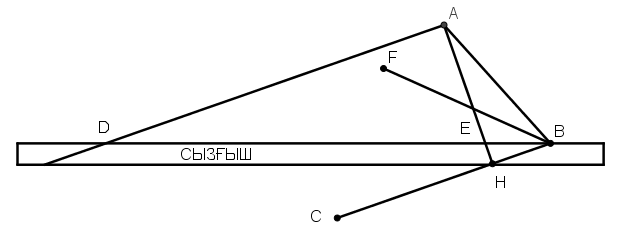
[12 – сурет].

 

[ХІІ] Доғаны тең үш бөлікке бөлу туралы. Егер ол ABD доғасын тең үш бөлікке бөлу керек десе, онда осы доға орналасқан дөңгелектің центрін табамыз. Бұл Е нүктесі болсын. А мен Е–ні, Е мен D–ны қосып, ABCD доғасын В мен С нүктелерінде қиып өтетін ЕВ және ЕС сызықтарымен AED бұрышын үш тең бөлікке бөлеміз. Сонда ABCD доғасы үш тең бөлікке АВ, ВС және СD¹⁸ доғаларына бөлінетін болады. Міне оның суреті [13 – сурет].

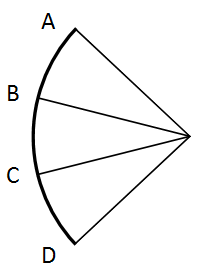
[13 – сурет].

 

[ХІІІ] Екі еселенген басқа үйге немесе шарға тең немесе басқа қатынаста алынған үй немесе шар салу туралы. Егер ол ұзындығы, ені, биіктігі өзара тең екі еселенген басқа үй болып табылатын квадрат үйді салу керек болса немесе басқа екі еселенген болып келген шарды салу, немесе қақ бөліп немесе басқа бір қатынастарда болып табылатын шарды қалай салу керек десе, онда үй ұзындығына және шар диаметріне тең АВ сызығын тұрғызамыз, екі еселенген  тік бұрыш бойынша АВ сызығына АС сызығын салып, DABC жазық фигурасын толықтырамыз. AD мен ВС диагоналдарын жүргіземіз. Олар F нүктесінде қақ бөлінеді. Олардың бағытында DC мен DB сызықтарын созамыз. Cызғыштың шетін А нүктесіне қоямыз да оны GC және EB  сызықтары бойынша [ол оларды Е және G нүктелерінде қиылысқанша] GF пен FE тең болатындай болғанша қозғайтын боламыз.  Сонда үйдің ұзындығы немесе шардың диаметрі ВЕ¹⁹ сызығы болады.  Міне оның суреті [14 – сурет].

 

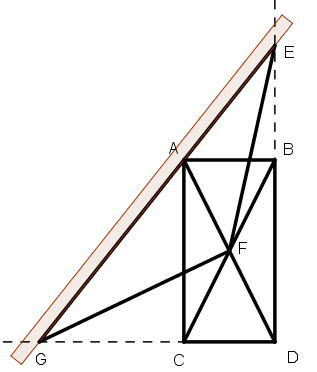
[14 – сурет].

 

[ХІV] Өртегіш айна жасау туралы. Егер біз күн сәулелерінің көмегімен бір қашықтықтан затты өртейтін айнаны жасағымыз келсе, онда алдымен айнаны айқындайтын (лекало) даяр үлгісін жасайық. Ол үшін  дөңгелек салайық, оның жарты диаметрі өртегіміз келетін заттың ара қашықтығының шамасына тең. Бұл АВС дөңгелегі болсын. Оның ADC диаметрін жүргізейік. DC сызығына С  нүктесінен бірнеше тең кесінділер салайық. Бұл кесінділер кіші болған сайын даяр үлгі жақсырақ және дәл болады. Бұл кесінділер CF, FH, HG, GE және ED болсын. D нүктесі арқылы [CD–ға] тік бұрыш бойынша E, G, H және F сызықтарын жүргізейік те оларды екі жағына да B, I, K, L және М нүктелеріне дейін созайық. C мен В, С мен I, С мен K, С мен L, С мен М нүктелерін қосайық. CM сызығына тең FN сызығын, CL–ге тең HX, CK–ға тең GO, CI–ге тең EP және СВ–ға тең DS сызығын салайық. C, N, X, O, P және S нүктелерін қосайық та осы сызық бойынша даяр үлгісін (лекало) жасайық. Сосын металдан, мысалы темірден, қоладан, мыстан немесе цинктен айна дайындайық та,  егер мүмкін болса оны ысып жалтыратайық. Егер айна қисық болып шықса, оны даяр үлгісі бойынша даяр үлгіні айнаға С нүктесі даяр үлгінің ортасына дәл келетіндей айнаның даяр үлгімен беттесуіне қол жеткізетіндей етіп даяр үлгіні айнаға беттестіріп түзетеміз. Сонда үлкен өртегіш күші²⁰ бар өртегіш айнаны аламыз. Міне оның суреті [15 – сурет].

 

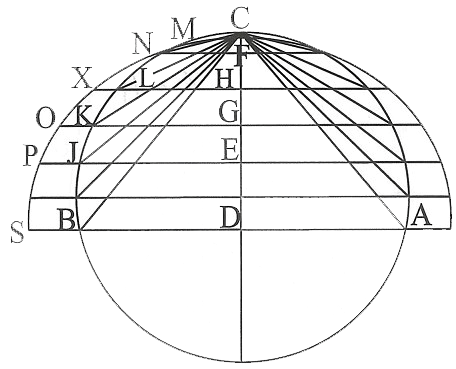
[15 – сурет].

 

[ХV] Өртегіш айна жасаудың екінші тәсілі.  Егер оны біз жасағымыз келсе, онда кез келген қашықтықты [оның жартысы АВ сызығы болсын] аламыз да, оны С нүтесіне дейінгі оның бағытына созамыз. В нүктесіне ВС–ға перпендикуляр DB сызығын қарама–қарсы екі жағына да орнатайық та, ВС сызығына өзара тең кіші сызықтарды BE, EG, GH және HC салайық. F нүктесінде АЕ–ні қақ бөліп, F центрінен FA  қашықтықта дөңгелек сызайық. Ол BD сызығын I нүктелерінде қияды. I нүктелерінен AC сызықтарына параллель IL сызықтарын жүргізейік те  Е нүктесінен BD сызығына параллель сызықты L нүктелеріне дейін жүргізейік. Сосын AG сызығын М нүктесінде қақ бөліп, М нүктесінен  МА қашықтықта дөңгелек сызамыз. Ол BD сызығын N нүктелерінде қияды. N нүктелерінен АС сызығына параллель NX сызықтарын Х нүктесіне дейін жүргіземіз. Сосын АН сызығын О нүктесінде қақ бөліп, О центрінен ОА қашықтықта дөңгелек сызамыз. Ол BD сызығын Р нүктелерінде қияды. Р нүктелерінен ВС–ға параллель Z нүктелеріне дейін сызықтар жүргізейік. B, L, X және Z нүктелерін сызықпен қосып, даяр үлгі аламыз. Егер біз даяр үлгіні тексеретін болсақ, оны В нүктесін айнаның ортасына орналастырамыз. Сонымен біз үлкен өртегіш күші бар өртегіш айна аламыз²¹.  Міне оның суреті [16 – сурет].

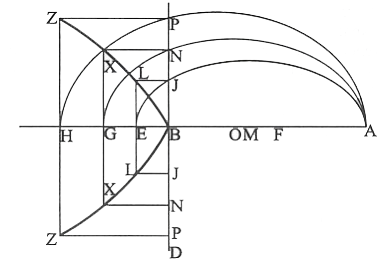
[16 – сурет].