Салу алгоритмі: Егер ол ABC үшбұрышына іштей қалай дөңгелек сызу керек десе

1.     В нүктесін центр етіп алып, АВ және ВС сызықтарында D және E [нүктелерін] белгілейміз.

2.     Осы [нүктелердің] әрқайсысын центр етіп қабылдап, G нүктесінде қиылысатын екі дөңгелек [тұрғызамыз]

3.     BG сызығын жүргіземіз.

4.     С нүктесін центр етіп аламыз және  АС және СВ сызықтарының бойынан H және F [нүктелерін] белгілейміз

5.     H және F нүктелерін центр етіп алып, I нүктесінде қиылысатын екі дөңгелек [тұрғызамыз]

6.     I және С-ны қосамыз.

7.     CI сызығы BG сызығымен K нүктесінде қиылысады.  

АВС⁴⁷ үшбұрышына іштей сызылған дөңгелектің центрі K-нүктесін аламыз.

 

 

 

 

 

 

 

 

 

 

 

 

 

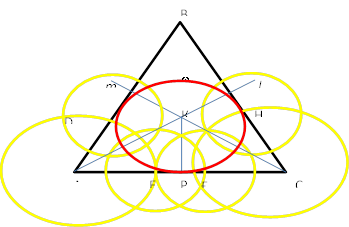Математикалық негіздеу: Берілген үшбұрыш тең қабырғалы болғандықтан, оның биссектриссаларының қиылысу нүктесі (үшбұрыштың тамаша нүктесі) биіктіктердің де, медианалардың да, орта перпендикулярларының да қиылысу нүктесі болып табылады.

Биссектрисалардың қиылысу нүктелерінен үшбұрыштың қабырғаларына жүргізілген биіктіктер өзара тең, сондықтан да бұл биіктіктер іштей сызылған шеңбердің радиусы болып табылады. Қабырғалардың барлығы шеңберге жанама, ал олар әр қашанда радиусқа перпендикуляр.

Талдау немесе басқа шешімнің бар болуы: Үшбұрыш тең қабырғалы болғандықтан, оның медианаларын немесе орта перпендикулярларын немесе биіктіктерінде жүргізу арқылы іштей сызылған шеңбердің центрін табуға болады.  

 

 [II] Осындай әдіспен басқа да тең қабырғалы және тең бұрышты фигураларға іштей дөңгелек сызуға болады: оның екі бұрышын қақ бөлеміз. Сызықтардың қиылысуы үшбұрышқа [төртбұрышқы, бесбұрышқы және т.с.с] іштей сызылған дөңгелектің центрін береді.