Салу алгоритмі (әл-Фараби бойынша):

1) Шеңб₁(A, r₁=AB);

2) Шеңб₂(B, r₁=AB);

3) Шеңб₁Окр₂=D и E;

4) DE;

5) Шеңб₃(A, r₂=AC);

6) Шеңб₄(C, r₂=AC);

7) Шеңб₃Шеңб₄=G и H;

8) GH;

9) DEGH=F

10) Шеңб₅(F, r₃=FA=FB=FC) – іздлініп отырған шеңбер;

11)  Шеңб_5.

Математикалық негіздеу: салу бойынша  және , бұдан: F –  үшбұрышының қабырғаларының орта перпендикуларларының қиылысу нүктесі және сырттай сызылған шеңбердің радиусы, дәлелдеу қажет болғаны да осы.

 

[ІІ] Үшбұрышқа сырттай сызылған дөңгелекті тұрғызудың екінші тәсілі. А және С нүктелерінен АВ және ВС сызықтарына AD және DC  перпендикулярларын тұрғызамыз; олар D нүктесінде қиылысады; BD жүргіземіз және оны Е нүктесінде қақ бөлеміз; Сонда Е - А, В және С нүктелері арқылы өтетін ізделінді дөңгелектің центрі⁴³. Міне оның суреті [75 - сурет].

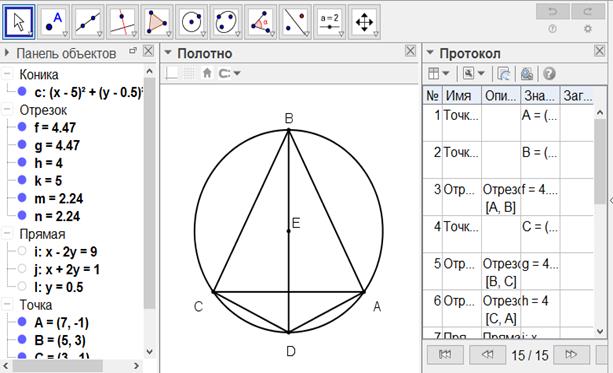
[75 - сурет]

Үшбұрышқа сырттай сызылған дөңгелекті тұрғызу (сурет 2).

Салу алгоритмі (әл-Фараби бойынша):

1) ; 2) ; 3) ; 4) BD;

5) ; 6) Окр(E, r=EA=EB=EC) – ізделініп отырған шеңбер.

Математикалық негіздеу: салу бойынша   және , яғни, іштей сызылған тікбұрыштар диаметрге тіреледі. Диаметрдің ортасы болатын E нүктесі – ізделініп отырған шеңбердің центрі. Ал, AE кесіндісі  – тікбұрышты үшбұрышының медианасы  –  сырттай сызылған шеңбердің радиусы болып табылады, дәлелдеу қажет болғаны да осы.

 

[ІІІ] Шаршыға сырттай сызылған дөңгелек жайлы. Егер ол ABCD шаршысына сырттай дөңгелекті қалай     сызу керек десе, он  да Е нүктесінде қиылысатын AC және BD диагональдарын жүргіземіз. Е - А, В, С және D⁴⁴ нүктелері арқылы өтетін дөңгелектің центрі. Міне оның суреті [76 - сурет].

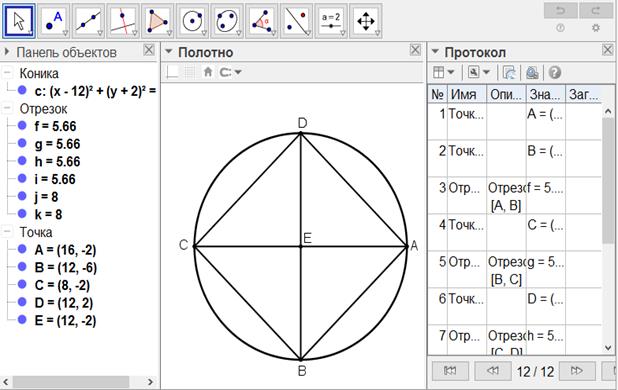
[76 - сурет]

Салу (әл-Фараби бойынша):

1) ;

2) ;

3) ;

4) E – ізделініп отырған шеңбер центрі;

5) Шеңб(E, r=EA=EB=EC=ED) – ізделініп отырған шеңбер.

Математикалық негіздеу: салу бойынша шаршы диаметрлері қиылысады. Шаршы диаметрінің қасиеті бойынша – диаметр қақ бөлінеді және сырттай сызылған шеңбердің центрімен. Ал,  кесінділері – шаршыға сырттай сызылған шеңбердің радиустары болып табылады, дәлелдеу қажет болғаны да осы.

 

[ІV] Бесбұрышқа сырттай сызылған дөңгелекті тұрғызу жайлы. Егер ол ABCDE бесбұрышына сырттай дөңгелекті қалай тұрғызамыз десе, онда А және В нүктелерін центр етіп алып, G және Н нүктесінлерінде қиылысатындай екі дөңгелек тұрғызамыз да, GH сызығын жүргіземіз. Ары қарай дәл осындай  А және Е нүктелерін центр етіп алып, I және K нүктелерінде қиылысатындай екі дөңгелек тұрғызамыз. GH сызығымен L нүктесінде қиылысатындай IK [сызығын]  жүргіземіз. Сонда L - А, В, С, D, E⁴⁵ нүктелері арқылы өтетін дөңгелектің центрі. Міне оның суреті [77 - сурет].

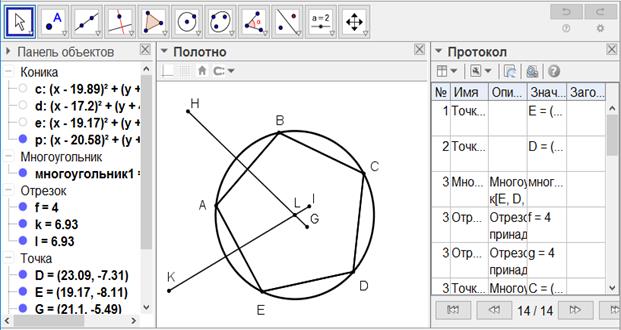
[77 - сурет]

Салу (әл-Фараби бойынша):

1) Шеңб₁(A,);

2) Шеңб₂(B, );

3) Шеңб₁Шеңб₂=G и H;

4) GH;

5) Шеңб₃(A, );

6) Шеңб₄(E, );

7) Шеңб₃ Шеңб₄=J және K;

8) JK;

9) GHJK=L

10) A, B, C, D, E Шеңб₅(L, r₃=LA=LB=LC=LD=LE) – ізделініп отырған шеңбер; 11)  Шеңб₅ – ізделініп отырған шеңбер.

Математикалық негіздеу: салу бойынша  және  – тең теңбүйірлі үшбұрыштар, яғни, . Сол тәрізді дәлелдейміз: , сонымен  -  нүктесімен бірдей қашықтықта жатыр. Бұдан Шеңб₅ дұрыс бесбұрышқа сырттай сызылған шеңбер болып табылады, дәлелдеу қажет болғаны да осы.

 

[V] Алтыбұрышқа сырттай сызылған дөңгелекті тұрғызу жайлы. Егер ол ABCDEG алтыбұрышына сырттай дөңгелекті қалай тұрғызамыз десе, онда А және В нүктелерінің әрқайсысын центр етіп алып, АВ қашықтықта Н нүктесінде қиылысатындай екі дөңгелек тұрғызамыз. Сонда H - А, В, С, D, E, G⁴⁶ нүктелері арқылы өтетін дөңгелектің центрі. Міне оның суреті [78- сурет].

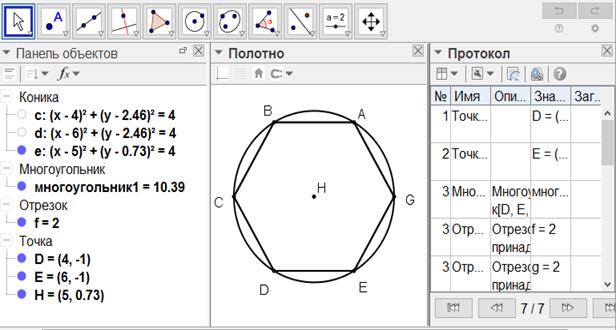
[78-сурет]

Салу (әл-Фараби бойынша):

1) Шеңб₁(A,);

2) Шеңб₂(B, );

 3) Шеңб₁Шеңб₂=H – дұрыс алтыбұрышқа сырттай сызылған шеңбер центрі; 10) A, B, C, D, E, G Шеңб₃(H, r₃=HA=HB=HC=HD=HE=HG) – ізделініп отырған шеңбер; 11)  Шеңб₃ – ізделініп отырған шеңбер.

Математикалық негіздеу: салу бойынша

  – теңбүйірлі үшбұрыштар, яғни . Сондықтан ,G - нүктесінен бірдей қашықтықта жатыр. Бұдан, Шеңб₃ дұрыс алтыбұрышқа сырттай сызылған шеңбер болып табылады, является описанной окружностью около правильного шестиугольника, дәлелдеу қажет болғаны да осы.

 

[VІ] Егер [теңқабырғалы] көпқабырғалы және көпбұрышты фигура берілсе, онда оған сырттай дөңгелек салу үшін жоғарыда бесбұрышқа сырттай дөңгелек салғанымыздай, қабырғаларын қақ бөліп, перпендикулярлар тұрғызамыз. Бұл тұрғызылымның  бесбұрышқа сырттай дөңгелек салудан еш айырмашылығы жоқ, қабырға саны көп немесе аз [фигуралар үшін].