Салу (аль-Фараби бойынша):

1) |;

2) ;

3) ;

4) 5)  6) ; 7)  – ізделініп отырған үшбұрыш.

Математикалық негіздеу: Доға  яғни, салу бойынша  (үш қабырғасы бойынша). Бұл үшбұрыштардың қабырғалары салу бойынша радиустарға тең. Бұдан В : және   екені анық.

Демек, , . Іргелес бұрыш . Сәкесінше   екенін табамыз. Яғни, орталық бұрыштарға тірелетін доғалар:  және іштей сызылған бұрыштар . Демек,  - дұрыс, яғни дәлелдеу қажет болғаны да осы.

Зерттеу: Берілген шеңберге мұндай үшбұрыштарды шексіз көп  іштей салуға болды, яғни олардың барлығы  өзара тең болады, олай болса есептің жалғыз шешімі бар.

 

[ІІ] Шеңберге сырттай сызылған үшбұрышты салу. Егер біз дөңгелекке сырттай сызылған теңқабырғалы үшбұрышты салғымыз келсе, онда оның ішіне теңқабырғалы АВС үшбұрышын сызамыз да, А, В және С нүктелерінің әрқайсысынан G, H және F нүктелерінде кездескенге дейін жанама сызықтар жүргіземіз. Сонда теңқабырғалы HGF35 үшбұрышын аламыз. Міне оның суреті [60 - сурет].

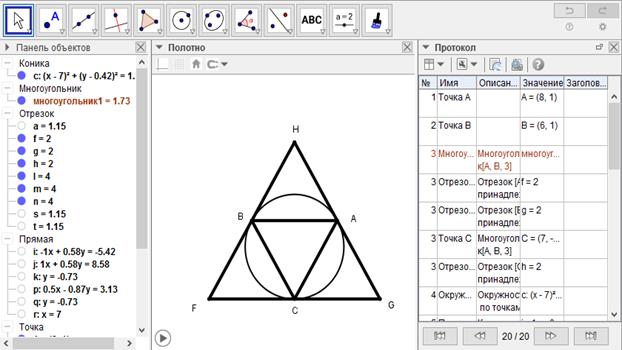
[60 - сурет].

Салу: Егер біз дөңгелекке сырттай сызылған теңқабырғалы үшбұрышты салғымыз келсе, онда

1.     Теңқабырғалы АВС үшбұрышын саламыз

2.     А, В және С нүктелерінің әрқайсысынан G, H және F нүктелерінде кездескенге дейін жанама сызықтар жүргіземіз.

Сонда теңқабырғалы HGF35 үшбұрышын аламыз

Математикалық негіздеу: қабырғалары салу бойынша радиустарына перпендикуляр. А центр сонымен қатар  бұл А үшбұрыштың қабырғасы,  салу бойынша шеңберге жанама болып табылады. Кесіндінің бір нүктесінен жүргізілген жанама қасиеті бойынша: . Тік бұрышты үшбұрыш теңдеуінен:  (екі катеті бойынша) бұдан олардың қабырғаларының теңдігі шығады: . Яғни,  дұрыс және сырттай сызылған, дәлелдеу қажет болып отырғаны да осы.

 

[ІІІ] Шеңберге іштей сызылған шаршыны салу. Егер ол дөңгелекке іштей сызылған теңқабырғалы және тең бұрышты төртбұрышты қалай салу керек десе, онда AB[C]D дөңгелегін тұрғызып, оның ішіне тік бұрыш бойынша қиылысатын АС және ВD диаметрлерін саламыз да AB, BC, CD және DA сызықтарын жүргіземіз. Сонда теңқабырғалы және тең бұрышты ABCD36 төртбұрышын аламыз. Міне оның суреті [61 - сурет].

 

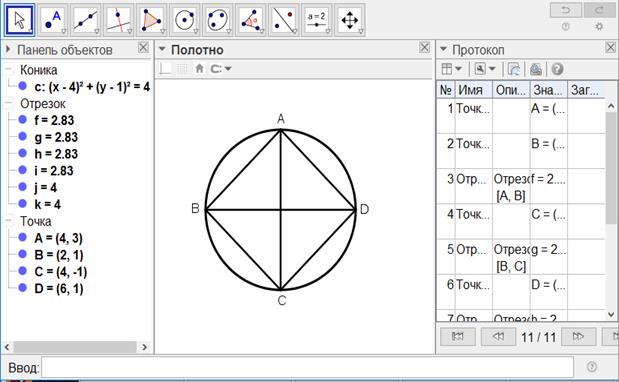
[61 - сурет]

Салу алгоритмі:

1.     AB[C]D дөңгелегін тұрғызамыз.

2.     Оның ішіне тік бұрыш бойынша қиылысатын АС және ВD диаметрлерін саламыз да AB, BC, CD және DA сызықтарын жүргіземіз.

Сонда теңқабырғалы және тең бұрышты ABCD36 төртбұрышын аламыз.

Математикалық негіздеу: салу бойынша  және  шеңбердің радиусына тең. Тікбұрышты үшбұрыштар теңдеуінен:  (екі катеті бойынша) бұдан олардың қабырғаларының теңдеуі: . Яғни, мұндай ромб шаршы болып табылады, дәлелдеу қажет болып отырғаны да осы.

 

[ІV] Егер ол ABCD дөңгелегінің жарты диаметріне тең циркуль ашасын пайдаланып, теңқабырғалы және тең бұрышты төртбұрышты дөңгелекке іштей қалай салу керек десе, онда АС диаметрін жүргіземіз. А нүктесін центр ретінде қабылдап циркуль ашасымен Е және G нүктелерін белгілейік те, Е мен G-ді қосайық. С нүктесін центр ретінде қабылдап АЕ қашықтықта H пен F-ті белгілейміз де H пен F-ті қосамыз. KG және IF сызықтарын жүргізейік, олар М нүктесінде қиылысады. М нүктесімен центрді қосып осы сызықты оның В мен D нүктелеріне дейінгі бағытында созайық. AB, BC, CD және DA сызықтарын жүргіземіз. Теңқабырғалы және тең бұрышты ABCD37 төртбұрышы шығады. Міне оның суреті [62- сурет].

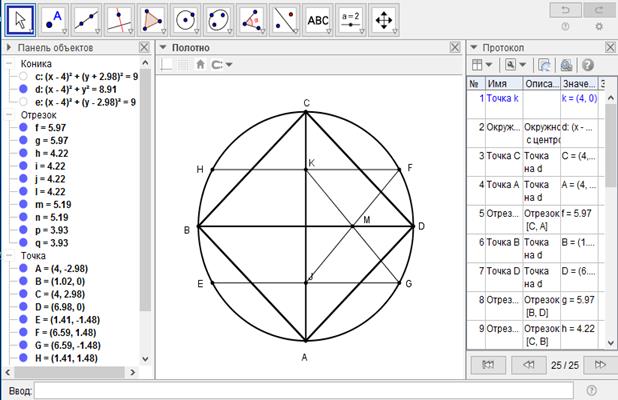
[62- сурет].

 

Берілген: R - шеңбердің радиусы. Шарт: салу барысында циркуль ашасын өзгертпеу керек.

Салу алгоритмі (аль-Фараби бойынша): циркуль ашасы туралы шартты ескеріп:

O                                   C

 

1) Шеңб1. (A; R=OC=OA);

2) Шеңб1Окр.=E   и G;  3) EG ; 4) Шеңб.2 (С; R=OC=OA);

5) Шеңб 2Окр.=H   и  F; 6) ; 7) ; 8); 9) OM  Шеңб. = B   және  D; 10) AB; 11)BC; 12) CD; 13) AD; 14) ABCD – ізделініп отырған шаршы (62-сурет).

Математикалық негіздеу: салуымыз бойынша AGFCHE дұрыс алты бұрыш болып шығады. Бұдан KFGJ тіктөртбұрыш екені көрініп тұр. Ал тіктөртбұрыштың диагональдары қиылысу нүктесінде қақ бөлінеді. Олай болса AC мен BD тік бұрышпен қиылысады. Яғни ABCD шаршы екені көрініп тұр.

 

[V] Егер қаласаңыз А және С нүктелерін центр ретінде қабылдап, Е, G, H және F нүктелерін белгілейік. АС сызығын I және К нүктелерінде қиып өтетін EG және HF сызықтарын жүргізейік. Центрлері осы нүктелер болатын циркульдің ашасындай қашықтықта L және М нүктелерінде қиып өтетін екі дөңгелек сызайық. L және М-ді өзара қосайық та [LM]-ді В мен D нүктелеріне дейін созайық. AB, BC, CD және DA сызықтарын жүргізейік. Теңқабырғалы және тең бұрышты ABCD төртбұрышын аламыз. Міне оның суреті [63 - сурет].

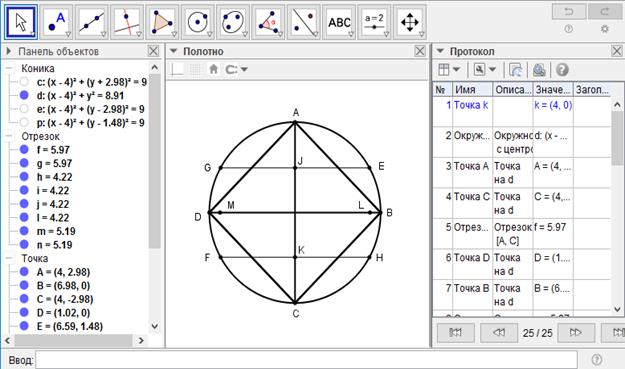
[63 - сурет]

Бұл IV-ні салудың басқа тәсілі (шарт бойынша іштей сызылған төртбұрыш)  (2-шешімі).

Салу (аль-Фараби бойынша): циркуль ашасы туралы шартты ескеріп, алдымен циркуль ашасын берілген кесіндіге тең етіп аламыз.

1) Шеңб. (O; R=OC=OA);

2) Шеңб1. (A; R);

3) Шеңб1Шеңб.=E  және  G; 3) EG ;

4) Шеңб.2 (С; R);

5) Шеңб.2 Шеңб.=H  және F;

6) ;

7) ;

8) Шеңб.3 (J; R);

9) Шеңб.4 (K; R);

10) Шеңб.3 Шеңб.4=M  және  L; 11) ML;

12) LM  Шеңб. = B  және  D; 13) AB;

14) BC; 15) CD; 16) AD;

17) ABCD – ізделініп отырған шаршы.

Математикалық негіздеу: Бұл жерде де алдыңғы есепке сүйенсек болады. Мұнда ML арқылы өтетін сызық AC сызығын тік бұрышпен қақ бөледі. Ал бұл сызықтың шеңбермен қиылысқан нүктелері шаршының төбелері болып табылады.

 

[VІ] Егер қаласаңыз Е, G, H және F нүктелерін центр ретінде қабылдап, I және К нүктелерінде қилысатын дөңгелектер салайық. IК сызығын жүргізейік, ол дөңгелекті В және D нүктелерінде қиып өтеді. Теңқабырғалы және тең бұрышты ABCD төртбұрышын аламыз. Міне оның суреті [64 - сурет].

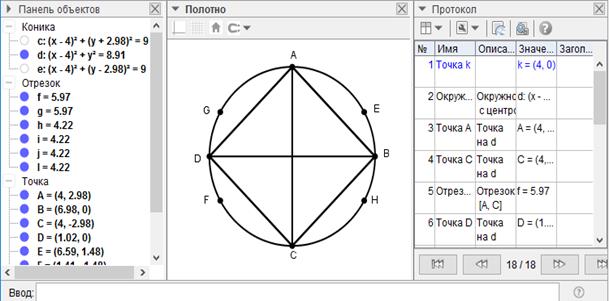
[64 - сурет]

Бұл IV-ті салудың басқа тәсілі (3-тәсіл).

Салу алгоритмі (аль-Фараби бойынша):

1) Шеңб. (O; R=OC=OA)|AC – диагональ;

2) Алдыңғы есептегідей нүктелерді белгілейміз: G, E, H, F;

3) Шеңб.1 (E; R);

4) Шеңб.2 (H; R);

5) Шеңб.1  Шеңб.2=J;

7) Шеңб.3 (G; R);

8) Шеңб.4 (F; R);

9) Шеңб.3  Шеңб.4=K;

10) JK;

11) JK Шеңб.= B және D;

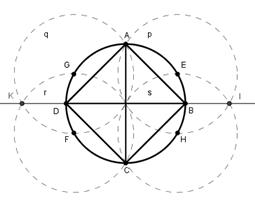12) ABCD – ізделініп отырған шаршы.

 

Математикалық негіздеу: Бұл жерде де алдыңғы есепке сүйенсек болады. Мұнда KI арқылы өтетін сызық AC сызығын тік бұрышпен қақ бөледі. Ал бұл сызықтың шеңбермен қиылысқан нүктелері шаршының төбелері болып табылады.

 

[VІІ] Егер қаласаңыз А, F және C, G нүктелерін қосайық. А, F және C, G нүктелерін қосатын сызықтар М нүктесінде қиылысады. Оны центрмен қосып ол сызықты B мен D нүктелеріне дейін созайық. Міне оның суреті [65 - сурет].

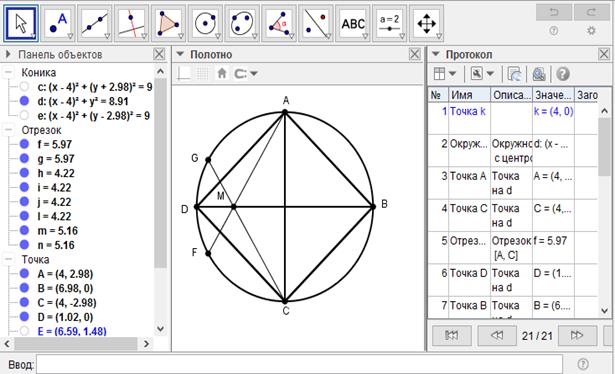
[65-сурет]

Бұл IV-ті салудың басқа тәсілі (4-тәсіл)

Салу алгоритмі (аль-Фараби бойынша):

1) Шеңб. (O; R=OC=OA)|AC – диагональ;

2) Алдыңғы есептегідей нүктелерді белгілейміз: G, E, H, F;

3) AF; 4) CG; 5) AFCG= M; 6) OM;

7) OM Шеңб.= B және D;

8) ABCD – ізделініп отырған шаршы.

Математикалық негіздеу: Бұл жерде де алдыңғы есепке сүйенсек болады. Мұнда M нүктесі мен центр арқылы өтетін сызық AC сызығын тік бұрышпен қақ бөледі. Ал бұл сызықтың шеңбермен қиылысқан нүктелері шаршының төбелері болып табылады.

 

[VІІІ] Шеңберге іштей сызылған бесбұрышты салу. Егер ол ABCD дөңгелегіне іштей сызылған тең қабырғалы және тең бұрышты бесбұрышты қалай салу керек десе, онда D нүктесін центр ретінде алып, онда ADC диаметрін жүргіземіз де D нүктесіне  DB перпендикулярын орнатамыз. AD-ны Е нүктесінде қақ бөліп Е нүктесін центр ретінде алып, ЕВ қашықтықта G нүктесін белгілейік те, В нүктесін центр ретінде алып, ВG қашықтықта F нүктесін белгілейік. Сонда дөңгелектің бестен бір бөлігі BF доғасын аламыз. IF, IK, KH және HB доғаларын BF доғасына тең ете жүргізіп, FB, BH, HK, KI, IF сызықтарын сызамыз. Сонда тең қабырғалы және тең бұрышты BFIKH38 бесбұрышын аламыз. Міне оның суреті [66 - сурет].

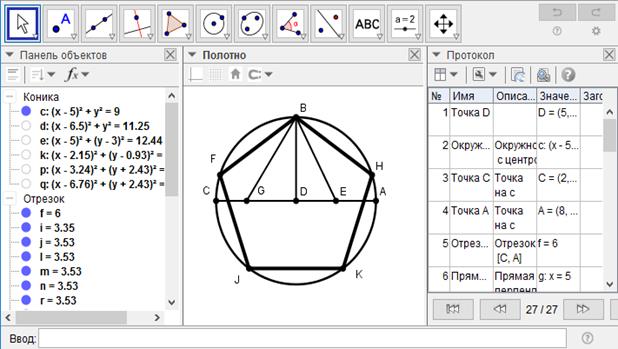
[66 - сурет]

 

Шеңберге іштей сызылған бесбұрышты салу.

Талдау. D нүктесі центрі және радиусы BD шеңберде  болғанда, бесбұрыш іштей сызылған делік. Есепте дұрыс бесбұрыштың қабырғаларын анықтау үшін тағы да екі шеңбер салу керек.

Салу алгоритмі (Әл-Фараби бойынша):

1) Шеңб. (D; ) |;

2) ;

3)  және ;

4) Шеңб.1 (E; r1=EB);

5) Шеңб.1AC= G;

6) Шеңб.2 (B; r2=BG);

7) Шеңб.2Окр.=F және K;

8)  - бесбұрыштың ізделініп отырған қабырғасы және ;

9) радиус -ті өзгертпей басқа қабырғаларын саламыз.

10) BFNMK – ізделініп отырған дұрыс бесбұрыш.

Мұнда: Шеңб. – шеңбер (дөңгелек жағша ішінде: центрі және радиусы, ал индексінде шеңберлерді послу реті көрсетілген).

Математикалық негіздеу: шеңберге сырттай сызылған дұрыс көпбұрыштың радиусын табудың жалпы формуласын білеміз

,

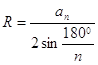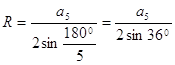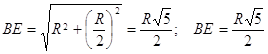бұдан: . Берілген шеңбердің радиусы  болсын, онда  , бұдан: ,   немесе   (1). Салу бойынша  және . Тікбұрышты -ден гипотенуза . Салу бойынша радиус ретінде:  Кесінділерді өлшеу қаситі бойынша: . Тікбұрышты -дан гипотенуза: .

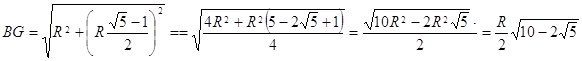Салу бойынша радиус ретінде: .

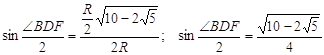Енді дәлелдеу керек:   (2). Теңқабырғалы үшбұрышын қарастырамыз, мұнда  сырттай сызылған шеңбердің . Косинустар теоремасы бойынша:  немесе                    (3).

Ендеше, (1) және (3) тең сол жақтары бар, бұдан, олардың оң жақтары да тең: . Дәлелдеу қажет болып отырғаны да осы, (2)-ні қараңыз.

Зерттеу: 1) шеңбер радиусын еркін таңдап алуға болады, онда бұл тәсілмен шексіз көп бесбұрыштар салуға болады. Бұл бесбұрыштар өзара тең (бұру қасиеті бойынша – қозғалысты түрлендіру), сондықтан берілген есептің жалғыз шешімі бар деп айту қабылданған.

 

[IX] Егер ол ABC дөңгелегіне іштей тең қабырғалы және тең бұрышты бесбұрышын егер D - дөңгелек центрі болса және  ашасы жарты диаметрге тең циркулмен қалай салу керек десе,  онда DA сызығына AB сызығына бесбұрыш салу кезінде салынған үшбұрышты  салайық. Бұл ADG  үшбұрышы болсын, ол ABC дөңгелегін C нүктесінде қияды. ABC доғасын B, H, E және C нүктелерінде төрт тең бөлікке бөліп, AC, CE, EH, HB және BA сызықтарын жүргізейік. Сонда тең қабырғалы және тең бұрышты ACEHBA39 бесбұрышын аламыз. Міне оның суреті [67 - сурет].

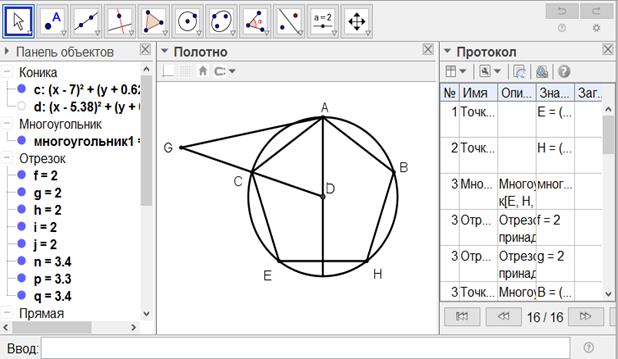
[67 - сурет]

 

Салу алгоритмі (Әл-Фараби бойынша):

1.      , мұнда ;

2.     Шеңб.1(A, r=AE);

3.     Шеңб.2(D, r=AE);

4.     Шеңб.1 Шеңб.2=G;

5.     GD Шеңб.=C;

6.     AC – бесбұрыш қабырғасы;

7.     Шеңб.4(C, r1=AC) Шеңб.=F;

8.     Шеңб.4(F, r1=AC) Шеңб.=H;

9.     Шеңб.4(H, r1=AC) Шеңб.=B;

10.           ACFHBA – ізделініп отырған дұрыс бесбұрыш.

 

[X] Шеңберге іштей салынған бесбұрышты салудың басқа жолы. DA сызығына DA сызығына тең AE перпендикулярын тұрғызып, DA сызығын G нүктесінде қақ бөлейік, GE жүргізіп, AD сызығына тең GH сызығын салайық, оны F нүктесінде қақ бөліп, DA-ны I нүктесінде қиятын FI перпендикулярын тұрғызайық. I нүктесін центр ретінде қабылдап, DA қашықтықта M және L белгілейік. Сонда ML доғасы - дөңгелектің бестен бірі. Міне оның суреті [68 - сурет].

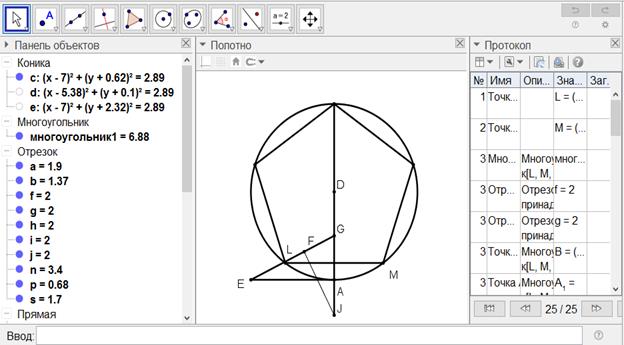
[68-сурет]

 

Шеңберге іштей салынған бесбұрышты салудың басқа жолы (IX-ды салудың (2-тәсіл))

Салу алгоритмі (аль-Фараби бойынша):

1) Шеңб.(D; r = DC=DA);

2) G | DG=GA;

3) Шеңб.1(G; r =DA);

4) Шеңб.Окр.1=H;

5) GH;

6);

7) ;

8) ;

9) ;

10) Шеңб.2(I; r=FI);

11) Шеңб. Шеңб.2=L және M;

12) LM – дұрыс бесбұрыштың қабырғасы.

 13) Шеңб.3(M; r3=LM);

14) Шеңб. Шеңб.3=B;

15) Шеңб.4(B; r3=LM);

16) Шеңб. Шеңб.4=C;

17) Шеңб.5(C; r3=LM);

18) Шеңб. Шеңб.5=N;

19) Шеңб.6(N; r3=LM);

20) Шеңб. Шеңб.6=L;

21) LMBCN – ізделініп отырған дұрыс бесбұрыш.

 

  [XІ] Шеңберге іштей сызылған алтыбұрышты салу. Егер ол дөңгелекке іштей сызылған тең қабырғалы және тең бұрышты  алтыбұрышты қалай салу керек десе, онда A және C нүктелерінің әрқайсысын центр ретінде алып, AC диаметрін жүргізіп, диаметрдің жартысына тең қашықтықта B және H, E және G белгілейік. AB, BE, EG, CG, GH және HA сызықтарын жүргізейік. Тең қабырғалы және тең бұрышты ABECGH40 алтыбұрышын аламыз. Міне оның суреті [69-сурет].

 

 

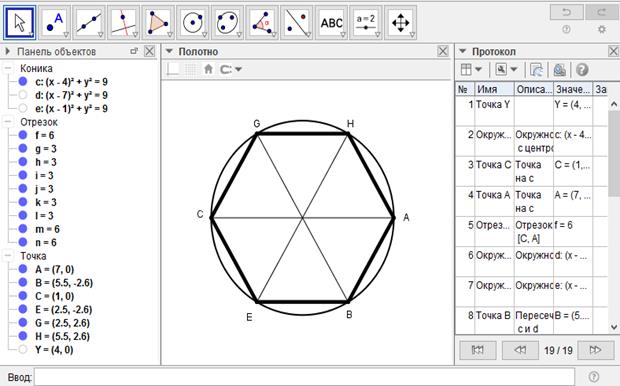
[69- сурет]

 

Салу алгоритмі (аль-Фараби бойынша):

1) Шеңб.(D; r =AD=DC);

2) Шеңб.1(C; r =AD);

3) Шеңб.Окр.1=B и H;

4) Шеңб.2(A; r =AD);

5) Шеңб.Окр.2=E және G; 12) AEBCHG – ізделініп отырған дұрыс алтыбұрыш.

Математикалық негіздеу: дұрыс үшбұрыштар үш қабырғасы бойынша тең (қабырғаласы бір шеңбердің радиустары болып табылады):

, бұдан, әр алты үшбұрыштың орталық бұрыштары тең . Ендеше, .

Салу бойынша . Дұрыс алтыбұрышқа сырттай сызылған шеңбер радиусының формуласы бойынша: .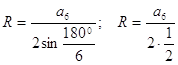

Бұдан: , Дәлелдеу қажет болып отырғаны да осы.

 

[XІІ] Шеңберге іштей сызылған жетібұрышты салу. Егер ол дөңгелекке іштей сызылған тең қабырғалы және тең бұрышты жетібұрышты қалай салу керек десе, онда ADC диаметрін жүргіземіз де, AD, яғни жарты диаметр қашықтықта B және E белгілеп, BE жүргізейік, ол AC сызығын G нүктесінде қияды. B нүктесін центр ретінде қабылдап, BG қашықтықта H нүктесін белгілейік. Сонда BH доғасы - дөңгелектің дәл емес, жуық жетіден бірі. Сондықтан, егер ABCE дөңгелегін BH доғасына тең бөліктерге бөліп, бөлу орындарын өз ара қоссақ, онда тең қабырғалы және тең бұрышты FBHIKLM41 жетібұрышын аламыз. Міне оның суреті [70-сурет].

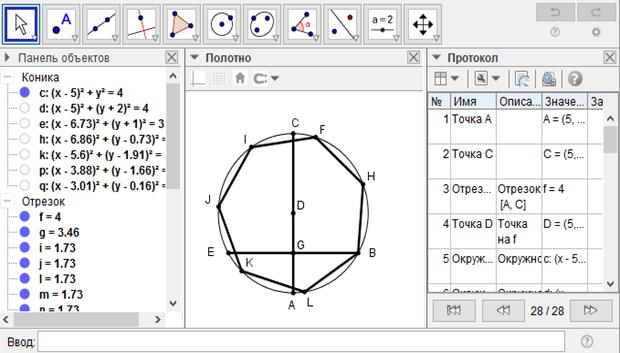
[70 - сурет]

 

Шешуі: Гаусс теоремасы бойынша, циркуль және сызғыштың көмегімен дұрыс n бұрышты салу үшін, n санының келесі түрде болғаны қажет және жеткілікті:  (1) – жай сандар, келсі түрде жазылады:  – . Егер  онда , егер   онда  және егер,  онда  және т.т.с.с. Бұдан, 3-, 5-, 17- дұрыс көпбұрыштар салуға болады, ал, 7, 9, 11, 13, 14 сандары сандарын көрсетілген түрде ұсыну мүмкін емес. Яғни, дұрыс 7-, 9-, 11-, 13-, 14-бұрыштық және осындай басқаларын циркуль мен сызғыш көмегімеен салу мүмкін емес.                                     

Жуықтап салу (Әл-Фараби бойынша): 1) Шеңб.(D; r =AD);

2) G | GA=GD;

3) Шеңб.1(A; r =AD);

4) Шеңб. Шеңб.1=B және E.;

5) Шеңб.2 (B; r1 = GB);

6) Шеңб.  Шеңб.2 = H;

7) BH – ізделініп отырған жуық дұрыс жетібұрыштың қабырғасы;

8) BHCMKIN – – ізделініп отырған жуық дұрыс жетібұрыш.

Мұнда: Шеңб. – шеңбер (дөңгелек жақша ішінде: центр және радиус, ал индексінде шеңберлерді салу реті көрсетілген).

Математикалық негіздеу: DA=DB=R болсын, онда салу бойынша . Тікбұрышты -тан,  Пифагор теоремасы бойынша: . Салу бойынша екінші шеңбердің радиусы ретінде: . 1) әл-Фараби айтуынша бұл жетібұрыштың қабырғаларының жуық мәнін анықтайды, яғни   (1) – салу бойынша. 2) дұрыс жетібұрышқа сырттай сызылған радиус формуласы бойынша келесіні аламыз: 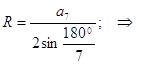 (2). Дәлелдейміз, жетібұрыштың қабырғалары салу бойынша және формула бойынша бір-бірінен айырмашылығы аз.:  немесе    . Абсолютті және салыстырмалы ауытқуы, сәйкесінше:  және . Жоғарыда айтылған салыстыруларды ескеріп, мұндай жетібұрышты аз абсолююті және салыстырмалы ауытқумен салуға болады. Яғни, шеңбер радиусын еркін  таңдауымызға болады, онда бұл тәрізді шексіз көп жетібұрыш салуға болады. Бұл жетібұрыштар бір біріне тең.

Бұдан, есептің жалғыз шешімі бар.

Мұнда: Шеңб. – шеңбер (дөңгелек жақша ішінде: центр және радиус, ал индексінде шеңберлерді салу реті көрсетілген).

 

[XIІІ] Шеңберге іштей сызылған сегізбұрышты салу. Егер ол дөңгелекке іштей сызылған тең қабырғалы және тең бұрышты  сегізбұрышты қалай салу керек десе, онда оған тең қабырғалы және тең бұрышты  төртбұрышты іштей саламыз да, әр доғаны қақ бөліп, бөлу орындарын жаңа нүктелерде түзу сызықтармен қосамыз. Тең қабырғалы тең бұрышты да сегізбұрыш аламыз. Міне оның суреті [71 - сурет].

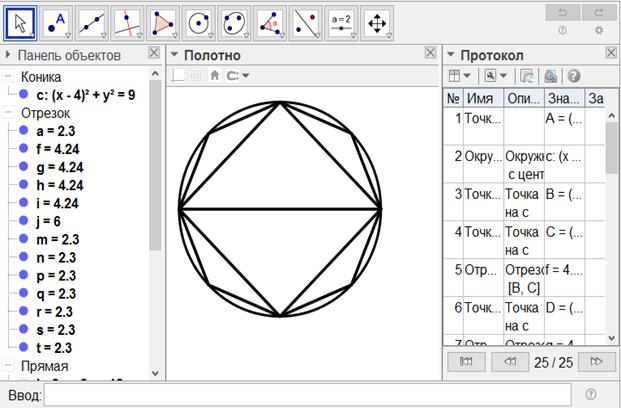
[71 - сурет]

 

Салу алгоритмі (Әл Фәрәби бойынша):

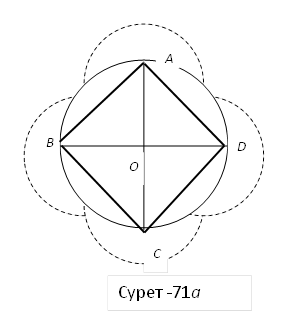
1) Шеңберге іштей төртбұрыш саламыз (сурет 13-а);

2)  AB, BC, CD жне  DA доғаларын қақ бөлеміз  және и бөлу нүтелері белгілейміз;

3)  AB доғасының ортасын E  нүктесімен белгілейміз;

4) доғасның ортасын G  нүктесімен белгілейміз;

5) CD доғасының ортасын H  нүктесімен белгілейміз;

6) AD доғасының ортасын   I  нүктесімен белгілейміз;

7) Кесінділермен нүктелерді қосамыз: A, E, B, G, C, H, D, I;

8) AEBGCHDI – ізделініп отырған іштей сызылған дұрыс сегізбұрыш.

 

 

 

 

 

 

 

 

 

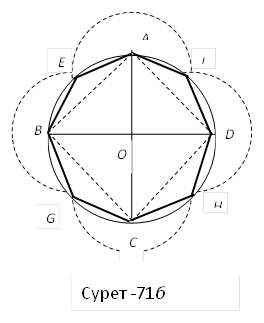
Математикалық негіздеу: салу бойынша барлық төбелер бір шеңберге тиісті. Сонымен қатар, теңқабырғалы үшбұрыштар үш қабырғасы бойынша тең (әр екі қабырғасы бір шеңбердің радиусы, ал үшінші қабырғалары салу бойынша тең):

 , бұдан, олардың төбелері бір шеңберде жатыр, ал AEBGCHDI – фигурасы, ізделініп отырған іштей сызылған сегізбұрыш, дәлелдеу қажет болып отырғаны да осы.

 

[XIV] Шеңберге іштей сызылған тоғызбұрышты салу. Егер ол дөңгелекке іштей сызылған [тең қабырғалы және тең бұрышты] тоғызбұрышты қалай салу керек десе,  дөңгелекке  тең қабырғалы   үшбұрышты іштей  салып, әр доғаны тең үш бөлікке бөлеміз де, бөлу орындарын түзу сызықтармен қосамыз.  Тең қабырғалы [тең бұрышты да] тоғызбұрыш аламыз. Міне оның суреті [72 - сурет].

 

[72 - сурет]

Задача 14-а. Покажем, несколько других построений, установленные другими ученными позже аль-Фараби.

1. Метод построения правильного вписанного девятиугольника комментатора и переводчика Евклида: Мордухай-Болтовского [2, с.: 364.]. Построим угол в  отдельно (рисунок 14-в) и построим:

 (рисунок 14-г).

4.Построим биссектрису OI угла

5. Построим: AI, IH и HC – стороны правильного девятиугольника;

6. Раствором циркуля равным AI построим другие стороны девятиугольника;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

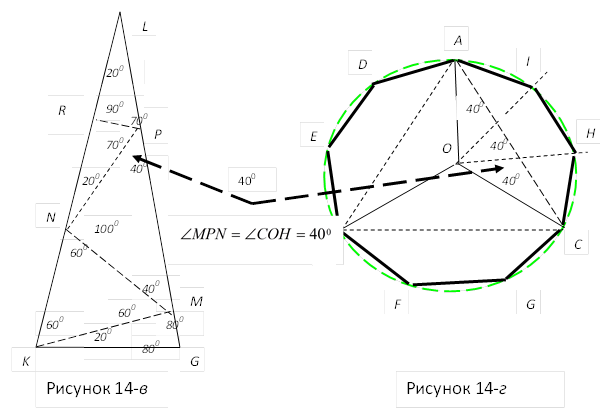
ADEBFGCHI – искомый приближенно правильный вписанный девятиугольник.

Так как построения угла в , тоже сводится к трисекцию угла в , это простроение тоже является приближенным.

Здесь заметим, теорему Лежандра: если правильный многоугольник существует, то существует и окружность проходящий через все его вершины.

Добавим, что из этого следует, что если окружность существует, то существуют и все правильные многоугольники имеющие вершины на окружности.

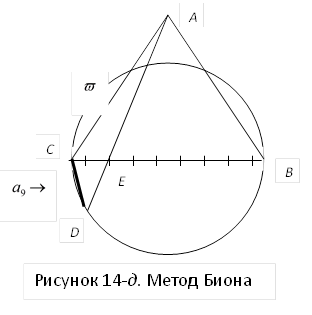Задача-14-б. 2. Прием Биона [2, с.: 364 ]. Если число стороны многоугольника представимо в виде: , где  и , то можно найти сторону вписанного правильного многоугольника следующим образом (рисунок 14-д).

1. Построить CB – диагональ окружности ;

2. Разделить диагональ на n равных частей с помощью теоремы Фалеса.

3.Построить равносторонний трегольник на диаметре.

4. Отметить вторую точку E деления в диаметре;

5. Соединить точку E с вершиной треугольника – A и продолжить прямую AE до пересечения с окружностью , обозначит точку пересечения, через букву D.

6. Соединить C и D, тогда CD – сторона правильного n-угольника.

На рисунке 14-д показано построение стороны правильного вписанного девятиугольника, т. к. девятиугольник удовлетворяет условию Дюрера: .. . нного никаоны правильного лжить до пересечения с окружностью, обозначит точку пересечения.

Задача 14-в. Метод Дюрера: «Рыбьи пузырь» (рисунок 14-е, 14-ж и 14-з)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

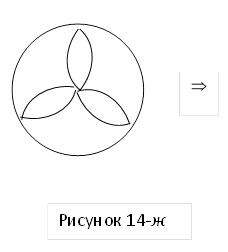
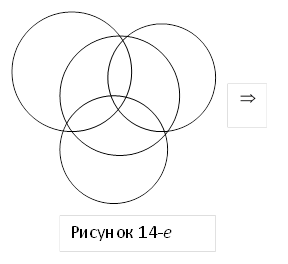
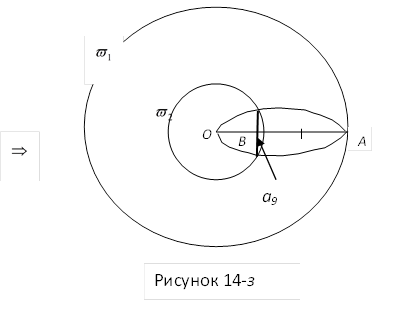
Здесь: фигура ОА – лист «рыбьего пузыря», ,  – отрезок равный стороне правильного девятиугольника. вписанного в окружность .

 

[XV] Шеңберге іштей салынған онбұрышты салу. Егер ол дөңгелекке іштей салынған онбұрышты қалай салу керек десе, онда егер қаласақ, оған іштей бесбұрыш салып, доғаның әрқайсысын қақ бөлеміз [де, бөлу нүктелерін сызықтармен қосамыз], іштей сызылған онбұрыш шығады. Егер қаласақ, алдыңғы салынғанға ұқсас іштей бесбұрыш саламыз да, сосын бұрынғыдай DG сызығын [саламыз]. Бұл онбұрыштың хордасы. Шеңберді DG сызығына тең бөліктерге бөлейік те, бөлу орындарын өзара түзу сызықтармен қосайық. Дөңгелекке іштей салынған тең қабырғалы [тең бұрышты да] онбұрыш42 шығады. Міне оның суреті [73 - сурет].

 

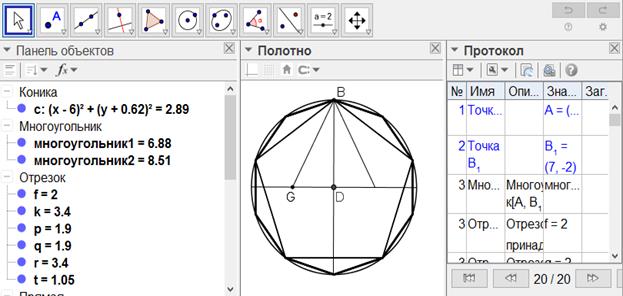
[73 - сурет]

Салу алгоритмі: Шеңберге іштей салынған онбұрышты салу. Егер ол дөңгелекке іштей салынған онбұрышты қалай салу керек десе, онда егер қаласақ,

1.     Оған іштей бесбұрыш саламыз

2.     Доғаның әрқайсысын қақ бөлеміз

3.     Бөлу нүктелерін сызықтармен қосамыз

4.     Іштей сызылған онбұрыш шығады.

5.     Егер қаласақ, алдыңғы салынғанға ұқсас іштей бесбұрыш саламыз да, сосын бұрынғыдай DG сызығын [саламыз].

6.     Бұл онбұрыштың хордасы. Шеңберді DG сызығына тең бөліктерге бөлейік те, бөлу орындарын өзара түзу сызықтармен қосайық. Дөңгелекке іштей салынған тең қабырғалы [тең бұрышты да] онбұрыш42 шығады.

Салу (аль-Фараби бойынша): 1) BFIKM – іштей сызылған дұрыс бесбұрыш.

2) Диаметрлер:; D-шеңбердің центрі (D; R=AD=DC)

1) ;

2) Шеңб1.(E; R=EB);

3) Шеңб.1AC=G;

4) Шеңб2.(B; R=BG);

5) Шеңб.Шеңб.2=F;

6) BF – BFIKM  іштей сызылған дұрыс бесбұрышының қабырғасы;

7) DG – іштей сызылған дұрыс онбұрышының қабырғасы;

8) Шеңб3.(B; R=DG);

9) Шеңб.Шеңб.3=P;

10) Шеңб4.(F; R=DG);

11) Шеңб.Шеңб.4=H;

12) Шеңб5.(I; R=DG);

13) Шеңб.Шеңб.5=J;

14) Шеңб6.(K; R=DG);

15) Шеңб.Шеңб.6=L;

16) Шеңб7.(M; R=DG);

17) Шеңб.Шеңб.7=N;

18) Соединяем вершины вписанного правильного пятиугольника и найданные точки:

P, H, J,L, N;

19) BPFHIJKLMN – искомый вписанный правильный десятиугольник.

Математикалық негіздеу: Зная общую формулу нахождения радиуса описанной окружности около правильных многоугольниковДұрыс көпбұрыштарға сырттай сызылған шеңбердің радусы 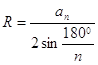 болатыны бізге белгілі. Олай болса: 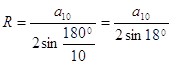. Мұнда болсын, сонда  ондай болса ,

  или  (1).

, ал есептің шарты бойынша . Тік бұрышты үшбұрышынан гипотенуза  . Салу бойынша радиус:  тең. Кесінділерді өлшеу қасиеті бойынша: . Салу бойынша . Бұл (1) формуладағы іштей сызылған дұрыс онбұрыштың қабырғасы, яғни:   (2) екенін дәлелдейік.

Теңбүйірлі үшбұрышын қарастырайық, мұнда шеңбердің радиусы . Косинустар теоремасына сүйенсек:

 немесе

 

          (3)

Алынған (3) өрнектің сол жақ бөлігі (1) өрнектің сол жақ бөлігімен сәйкес келеді.

Сәйкесінше оң жақ бөліктері де өзара тең: