Салудың алгоритмі:

1.     A және В нүктелерін центр етіп алып, АВ қашықтықта шеңберлер жүргіземіз.

2.  Бұл шеңберлер С нүктесінде қилысады.

3.  С нүктесін А және В нүктелерімен СА және СВ түзу сызықтармен қосамыз.

Сонда АВС үшбұрышы тең қабырғалы болып табылады.

Математикалық негіздеу: Тікбұрышты үшбұрышқа сырттай сызылған шеңбердің ценрі гипотенузаның  қақ ортасында жатады.

 

[ІІ] Шаршы салу туралы. Егер ол АВ сызығына тең қабырғалы [және тең бұрышты] төртбұрышты қалай тұрғызамыз десе, онда А мен В нүктелерінің әрқайсысына перпендикуляр өзара тең АВ сызықтарын орнатамыз. Ол - АС мен ВD сызықтары. С мен D-ны қосып  тең қабырғалы [және тең бұрышты] ABCD²³ төртбұрышын аламыз. Міне оның суреті [49 - сурет].

[49 - сурет]

Салудың алгоритмі:

1.  А және В төбелеріне АВ-ға тең болатындай АС және BD перпендикулярларын тұрғызамыз.

2.   С және D нүктелерін қосып, ABCD тең қабырғалы (және тең бұрышты) төртбұрышын саламыз.

Сонда АВСD төртбұрышы тең қабырғалы (және тең бұрышты)  болып табылады.

Математикалық негіздеу: Шеңберге жүргізілген жанама радиусқа перпендикуляр болады.

 

[ІІІ] Бесбұрышты салу туралы. Егер ол АВ сызығында тең қабырғалы бесбұрышты қалай тұрғызайық десе, онда В нүктесіне АВ-ға тең ВС перпендикулярын орнатамыз. АВ [сызығын] D нүктесінде қақ бөліп, D нүктесін центрі ретінде DC қашықтықта CE доғасын сызамыз да, АВ сызығын Е нүктесіне дейін созамыз. Сосын А мен В нүктелерінің әрқайсысын центрі ретінде алып АЕ қашықтықта доғалар сызамыз. Олар G нүктесінде қиылысады. AG және BG  сызықтарын жүргізейік. ABG үшбұрышын - бесбұрыштың үшбұрышын аламыз. Бұл көптеген салуларда қажет болады. Содан соң А мен G нүктелерін центрлер ретінде алып, АВ қашықтықта доғалар сызамыз. Олар Н нүктесінде қиылысады. Сосын центрлері ретінде В мен G нүктелерінен F нүктесінде қиылысатын доғалар сызамыз.  AH, HG, GF және FB сызықтарын жүргізіп, тең қабырғалы, тең бұрышты ABFGH²⁴ бесбұрышын аламыз. Міне оның суреті [50 - сурет].

 

[50 - сурет]

Салудың алгоритмі:

Егер ол АВ сызығында тең қабырғалы бесбұрышты қалай тұрғызайық десе, онда

1.     В нүктесіне АВ-ға тең ВС перпендикулярын орнатамыз.

2.     АВ [сызығын] D нүктесінде қақ бөлеміз

3.     D нүктесін центрі ретінде алып, DC қашықтықта CE доғасын сызамыз

4.     АВ сызығын Е нүктесіне дейін созамыз.

5.     А мен В нүктелерінің әрқайсысын центрі ретінде алып АЕ қашықтықта доғалар сызамыз.

6.     Олар G нүктесінде қиылысады. AG және BG  сызықтарын жүргіземіз. Сонда ABG үшбұрышын - бесбұрыштың үшбұрышын аламыз. Бұл көптеген салуларда қажет болады.

7.     Содан соң А мен G нүктелерін центрлер ретінде алып, АВ қашықтықта доғалар сызамыз.

8.     Олар Н нүктесінде қиылысады. Сосын центрлері ретінде В мен G нүктелерінен F нүктесінде қиылысатын доғалар сызамыз.

9.     AH, HG, GF және FB сызықтарын жүргізіп, тең қабырғалы, тең бұрышты ABFGH²⁴ бесбұрышын аламыз.

Математикалық негіздеу:  Дұрыс бесбұрыштың диагональдарының ұзындығы   екендігі белгілі. Ал, берілген алгоритм бойынша AB қабырғасын -ға тең деп алсақ,     Яғни берілген алгоритм бойынша сызылған бесбұрыш дұрыс бесбұрыш болып табылады.

 

[IV] Егер ол АВ сызығына тең циркуль ашасымен ғана, оның күйі өзгермейтіндей етіп  АВ сызығына тең қабырғалы бесбұрыш тұрғыз десе, онда АВ сызығына оған перпендикуляр АВ сызығына тең ВС сызығын орнатамыз.  АВ сызығын D нүктесінде қақ бөліп, С-мен қосамыз да D нүктесін центр ретінде алып, АВ қашықтықта DC сызығында I нүктесін белгілейміз, DI-ді K нүктесінде қақ бөліп, АВ сызығын Е нүктесінде қиып өтетін K нүктесіне KE перпендикулярын тұрғызамыз. Ары қарай  А мен Е нүктелерінің әрқайсысынан центрлері ретінде АВ қашықтықта доғалар сызамыз. Олар М нүктесінде қиылысады. ВМ-ді жүргізіп, оны G-ға дейін оның бағытында созамыз да, MG-ді АВ сызығына тең етеміз. А мен G -ді қосамыз. А мен G-ді центрлер ретінде қабылдап, АВ қашықтықта Н нүктесін белгілейік. B мен G нүктелерін центрлер ретінде қабылдап, АВ қашықтықта А нүктесін белгілейік. AH, HG, GF және FB сызықтарын жүргізейік. Тең қабырғалы AFBGH²⁵ бесбұрышы шығады. Міне оның суреті [51-сурет].

[51 - сурет]

Салудың алгоритмі:

1.     АВ сызығына оған перпендикуляр АВ сызығына тең ВС сызығын орнатамыз. 

2.     АВ сызығын D нүктесінде қақ бөліп, С-мен қосамыз да D нүктесін центр ретінде алып, АВ қашықтықта DC сызығында I нүктесін белгілейміз

3.     DI-ді K нүктесінде қақ бөліп, АВ сызығын Е нүктесінде қиып өтетін K нүктесіне KE перпендикулярын тұрғызамыз.

4.     А мен Е нүктелерінің әрқайсысынан центрлері ретінде АВ қашықтықта доғалар сызамыз. Олар М нүктесінде қиылысады.

5.     ВМ-ді жүргізіп, оны G-ға дейін оның бағытында созамыз да, MG-ді АВ сызығына тең етеміз.

6.     А мен G -ді қосамыз.

7.     А мен G-ді центрлер ретінде қабылдап, АВ қашықтықта Н нүктесін белгілейік.

8.      B мен G нүктелерін центрлер ретінде қабылдап, АВ қашықтықта А нүктесін белгілейік. AH, HG, GF және FB сызықтарын жүргіземіз.

Сонда тең қабырғалы AFBGH²⁵ бесбұрышы шығады

Математикалық негіздеу: Дұрыс бесбұрыштың диагональдарының ұзындығы   екендігі белгілі. Ал, берілген алгоритм бойынша AB қабырғасын -ға тең деп алсақ,     Яғни берілген алгоритм бойынша сызылған бесбұрыш дұрыс бесбұрыш болып табылады.

 

[V] Алты бұрышты салу туралы. Егер ол АВ сызығына тең қабырғалы және [тең бұрышты] алты бұрыш тұрғыз десе, онда ол үшін тең қабырғалы АВС үшбұрышын тұрғызамыз. АС мен ВС сызықтарын олардың бағыттарында Е мен G нүктелеріне дейін созайық. ВС-да тағы бір тең қабырғалы ВСD үшбұрышын тұрғызайық. DC сызығын оның бағытында Н нүктесіне дейін созып, СЕ, CG және СН сызықтарын СА сызығына тең етеміз де, DE, EG, GH және НА сызықтарын жүргіземіз. Тең қабырғалы және тең бұрышты ABDEGH²⁶ алты бұрышы шығады. Міне оның суреті [52 - сурет].

[52 - сурет]

 

Салудың алгоритмі:

1-қадам. AB  кесіндісі арқылы дұрыс ABC үшбұрышын саламыз.

2-қадам. C нүктесі арқылы AC мен BC кесінділерін бір бағытта AB кесіндісінің ұзындығына тең ұзындыққа созамыз.

3-қадам. Созылған кесінділердің ұштарын D және E деп белгілеп, оларды қосамыз.

4 -қадам. AC  кесіндісі арқылы дұрыс ACG үшбұрышын саламыз.

5-қадам. C нүктесі арқылы CG кесіндісін  AB кесіндісінің ұзындығына тең ұзындыққа созып, оның ұшын K деп аламыз.

6-қадам. G мен D-ны, E мен K-ны және K мен B-ны қосамыз.

 

Математикалық негіздеу: Дұрыс алтыбұрыштың ішкі бұрышы 120⁰ тең болады. Салынған алтыбұрыштың қабырғаларының теңдігі, AGC, GCD, DEC, ECK және KCB үшбұрыштарының өзара тең дұрыс үшбұрыш болатындығынан шығады. Ал, дұрыс үшбұрыштың ішкі бұрышы 60⁰-қа тең болғандықтан, салынған алтыбұрыштың әрбір ішкі бұрышы 120⁰-қа тең екендігі шығып тұр. Яғни берілген алгоритм бойынша сызылған алтыбұрыш дұрыс алтыбұрыш болып табылады.

 

[VI] Жеті бұрышты салу туралы. Егер ол АВ сызығына тең қабырғалы жеті бұрышты тұрғыз десе, онда ВС сызығын АВ сызығына тең етіп, АС сызығына тең қабырғалы DАС үшбұрышын тұрғызамыз да бесінші тарауда көрсетілгендей АВС үшбұрышына сырттай дөңгелек сызамыз. Онда АВ сызығына тең АЕ сызығын-хорданы жүргізіп G нүктесінде АЕ-ні қақ бөлеміз, GH перпендикулярын орнатып, оны дөңгелек шеңберіне дейін созамыз. АВ-ны F нүктесінде қақ бөліп, оған GH перпендикулярына тең FI перпендикулярын тұрғызайық. А, В және I нүктелері арқылы ABI дөңгелегін жүргізіп [оған] АВ доғасына тең АК, KL, LI, IM, MN және NB доғаларын саламыз. АК, KL, LI, IM, MN және NB сызықтарын жүргізейік; бұл тең қабырғалы және тең бұрышты жеті бұрыш²⁷. Міне оның суреті [53 - сурет].

 

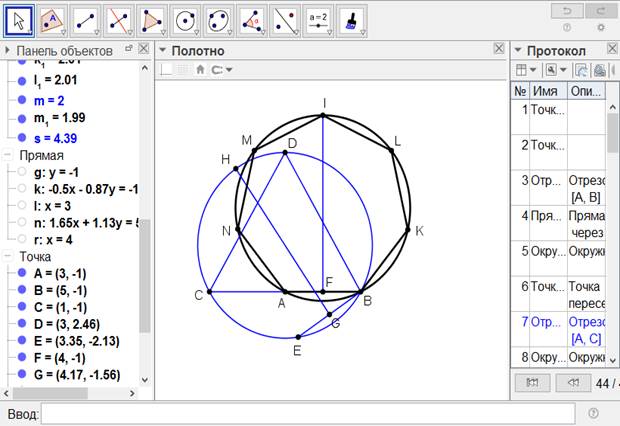
[53 - сурет]

 

Салудың алгоритмі:

1-қадам. АВ кесіндісін АВ =AC болатындай C нүктесіне созамыз.

2-қадам.   CB кесіндісі арқылы дұрыс (дұрыс үшбұрыш салу алгоритмін пайдаланып)  BCD үшбұрышын саламыз

3-қадам.  сырттай w1 шеңберін саламыз

4-қадам. B нүктесінен BE=AB болатындай  w1  шеңберіне BЕ хордасын саламыз және оның қақ ортасын G деп аламыз.

5-қадам. G нүктесінен BE хордасына перпендикуляр кесінді жүргізіп, оның w1 шеңберімен қыйылысу нуктесін H деп аламыз.

6-қадам.АВ кесіндісінің центрін F деп алып, ол нүктеден AB-ға ұзындығы GH кесіндісіне тең болатындай FI перпендикулярын саламыз.

7-қадам. А, В және I нүктелері арқылы w2 шеңберін сызамыз.

8-қадам.  w2 шеңберіне B нүктесінен бастап, ұзындығы AB кесіндісінің ұзындығына тең болатын, BK, KL, LI, IM, MN және NA хордаларын сызамыз.

 

Математикалық негіздеу: AB=BE, GH=FI, HG мен EB перпендикуляр, ал FI мен AB перпендикуляр және AF, FB, EG,GB кесінділері өзара тең болғандықтан w1 шеңбері мен w2 шеңберінің радиустері тең екендігі шығады. Алдымен w1 шеңберінің радиусын анықтап алайық. w1 шеңбері BCD дұрыс үшбұрышына сырттай сызылған шеңбер болғандықтан, оның радиусы дұрыс үшбұрышқа сырттай сызылған шеңбердің радиусының формуласына сәйкес төмендегідей болады;

                           R_w1=BC/                           (2.6)

AB кесіндісін бірлік кесінді деп алатын болсақ, BC=2AB=2, сонда шығатыны:

                            R_w1=2/                              (2.7)

 Келесі кезекте қабырғасы бірлік кесінді деп алынған дұрыс жетібұрыш бар деп алып, оған сырттай сызылған шеңбердің радиусын анықтайық. Қабырғасы a болатын дұрыс n бұрышқа сырттай сызылған шеңбердің радиусының формуласы төмендегідей болады:

                        R=                                 (2.8)  

Сонда, қабырғасы бірлік кесінді болатын, дұрыс жетібұрышқа сырттай сызылған шеңбердің радиусының мәні:

                         R=                                  (2.9)

 

   Берілген алгоритм бойынша сызылған жетібұрыш дұрыс жетібұрыш болып табылады, егер (7.2) теңдігі анықталған радиус пен (7.4) теңдігі анықталған радиустың мәндері бірдей болса. Ал бұл аталған мәндер sin(/4  шамасына тең болса ғана өзара тең болып табылады. Енді бұл аталған мәндердің әртүрлі дәлдікпен алынған сан мәндерін салыстыру кестесін келтірейік.

 

 

sin(/4  шамаларының әртүрлі дәлдіктегі мәндері

 

=10-1 /4≈0.433035714285714 sin(π/7)(π/7)≈0.433732732495189 (sin(π/7)-/4)≈0.000697018209475   e=10-2 /4≈0.433012702503682 sin(π/7)≈0.433884464751980 (sin(π/7)-/4)≈0.000871762248298   e=10-3 /4≈0.433012702503682 sin(π/7)≈0.433884464751980 (sin(π/7)-/4)≈0.000871762248298   e=10-4 /4≈0.433012702503682 sin(π/7)≈0.433883737085629 (sin(π/7)-/4)≈0.000871034581947   e=10-5 /4≈0.433012701892219 sin(π/7)≈0.433883737085629 (sin(π/7)-/4)≈0.000871035193410   e=10-6 /4≈0.433012701892219 sin(π/7)≈0.433883737085629 (sin(π/7)-/4)≈0.000871035193410

e=10-7 /4≈0.433012701892219 sin(π/7)≈0.433883739121281 (sin(π/7)-/4)≈0.000871037229061   e=10-8 /4≈0.433012701892219 sin(π/7)≈0.433883739121281 (sin(π/7)-koren)≈0.000871037229061   e=10-9 /4≈0.433012701892219 sin(π/7)≈0.433883739117553 (sin(π/7)-/4)≈0.000871037225334   e=10-10 /4≈0.433012701892219 sin(π/7)≈0.433883739117553 (sin(π/7)-koren)≈0.000871037225334

 

[VIІ] Сегіз бұрышты салу туралы. Егер ол АВ сызығына тең қабырғалы сегіз бұрышты қалай тұрғызу керек десе, онда АВ-ны оның бағытында С мен D нүктелеріне дейін созып А мен В нүктелерінің әрқайсысы үшін тікбұрыштың жартысына тең ЕАС және GBD бұрыштарын саламыз. АЕ және BG сызықтарының әрқайсысын АВ сызығына тең етіп алып Е мен G нүктелерінің әрқайсысынан DC сызығына ЕС және GD перпендикулярын түсіреміз де CHKD шаршысын толықтырамыз. HI, HF, KL және KM сызықтарының әрқайсысын СЕ сызығына тең етіп алып I және F,  L және M-ді қосамыз. Тең қабырғалы ABGMLFIE²⁸ сегіз бұрышы шығады. Міне оның суреті [54 - сурет].

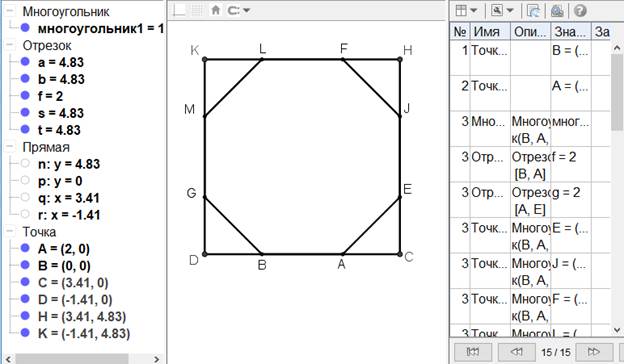
[54 сурет].

 

Салудың алгоритмі:

Егер ол АВ сызығына тең қабырғалы сегіз бұрышты қалай тұрғызу керек десе, онда

1.     АВ-ны оның бағытында С мен D нүктелеріне дейін созамыз.

2.     А мен В нүктелерінің әрқайсысы үшін тікбұрыштың жартысына тең ЕАС және GBD бұрыштарын саламыз.

3.     АЕ және BG сызықтарының әрқайсысын АВ сызығына тең етіп аламыз.

4.     Е мен G нүктелерінің әрқайсысынан DC сызығына ЕС және GD перпендикулярын түсіреміз.

5.     CHKD шаршысын толықтырамыз.

6.     HI, HF, KL және KM сызықтарының әрқайсысын СЕ сызығына тең етіп аламыз.

7.     I және F,  L және M-ді қосамыз. Сонда тең қабырғалы ABGMLFIE²⁸ сегіз бұрышы шығады.

Математикалық негіздеме:

<DBC=45⁰, <EAC=45⁰;

AB=EA, CD=AB;

<DCH=90⁰, <KDC=90⁰;

HI=CE, HF=CE, KL=CE және KM= СЕ болғандықтан MG=GB=BA=AE=EJ=JF=FL=LM, ал  <EAB=<ABG=<BGM=<GML=<MLF=<LFJ=<FGE=<JEA=135⁰, яғни бұл дұрыс сегізбұрыш болып табылады.

 

 

[VIІІ] Егер ол АВ сызығына тең циркуль ашасымен ғана, оның күйі өзгермейтіндей етіп,  АВ сызығына тең қабырғалы сегіз бұрыш тұрғыз десе, онда АВ сызығына тең қабырғалы және тең бұрышты ABCD төртбұрышын тұрғызып, СА және BD сызықтарын жүргіземіз де, олардың бағыттарында Е және G нүктелеріне дейін созамыз. АЕ мен BG сызықтарының әрқайсысын АВ сызығына тең етіп алып EG-ны қосамыз, EG сызығына АВ сызығына тең [EI және GM] перпендикулярларын орнатамыз да M және I-ді қосамыз. ЕІ мен GM сызықтарының әрқайсысын олардың бағыттарында К және Н нүктелеріне дейін созамыз да, IMK және MIH бұрыштарының әрқайсысын MLF сызықтарымен қақ бөлеміз. ML және ІF сызықтарының әрқайсысын АВ сызығына тең етіп алып FL-ді қосайық.  Тең қабырғалы тең бұрышты ABGMLFIE²⁹ сегіз бұрышы шығады. Міне оның суреті [55 - сурет].

[55 сурет].

Салудың алгоритмі: Егер ол АВ сызығына тең циркуль ашасымен ғана, оның күйі өзгермейтіндей етіп,  АВ сызығына тең қабырғалы сегіз бұрыш тұрғыз десе, онда

1.     АВ сызығына тең қабырғалы және тең бұрышты ABCD төртбұрышын тұрғызамыз

2.     СА және BD сызықтарын жүргіземіз де, олардың бағыттарында Е және G нүктелеріне дейін созамыз.

3.     АЕ мен BG сызықтарының әрқайсысын АВ сызығына тең етіп алып EG-ны қосамыз

4.     EG сызығына АВ сызығына тең [EI және GM] перпендикулярларын орнатамыз

5.     M және I-ді қосамыз.

6.     ЕІ мен GM сызықтарының әрқайсысын олардың бағыттарында К және Н нүктелеріне дейін созамыз

7.     IMK және MIH бұрыштарының әрқайсысын MLF сызықтарымен қақ бөлеміз.

8.     ML және ІF сызықтарының әрқайсысын АВ сызығына тең етіп алып FL-ді қосамыз. Сонда тең қабырғалы тең бұрышты ABGMLFIE²⁹ сегіз бұрышы шығады.

Математикалық негіздеме: Салынған сегізбұрыштың қабырғаларының ұзындықтарының теңдігі, берілген алгоритмнің қадамдарынан айқын көрініп тұр. Енді бұл сегізбұрыштың ішкі бұрыштарының әр қайсысы 135⁰-қа тең екендігін дәлелдеуіміз керек.

ABCD дұрыс төртбұрыш болғандықтан:

<BAC=45⁰, <ABD=45⁰

Бұдан шығатыны:

<EAB=180⁰-45⁰=135⁰,  <GBA=180⁰-45⁰=135⁰

AB мен EG кесінділері параллел болғандықтан:

<AEG=<BAC=45⁰, <BGE=<ABD=45⁰

Бұдан шығатыны:

<IEA=90⁰+45⁰=135⁰,  <MGB=90⁰+45⁰=135⁰

FIM және HMI бұрыштары тік бұрышты қақ бөлетіндіктен:

<FIE=90⁰+45⁰=135⁰,  <LMG=90⁰+45⁰=135⁰

Яғни берілген алгоритм бойынша сызылған сегізбұрыш дұрыс сегізбұрыш болып табылады.

 

[IX] Тоғызбұрышты салу туралы. Егер ол АВ сызығына тең қабырғалы және тең бұрышты тоғыз бұрыш тұрғызу керек десе, онда центрі G нүктесі болатын кез келген өлшемді  CDE дөңгелегін сызып, ондағы С нүктесін белгілеп оны центр ретінде қабылдайық та дөңгелектен жарты диаметрлік қашықтықта Е мен D нүктелерін белгілейік. DE доғасын тең үш бөлікке бөлейік. Сондай доғаның бірі EH болсын. EG, EH және HG сызықтарын жүргізіп, EG мен HG сызықтарының арасында АВ сызығына тең және ЕН сызығына параллель FI сызығын саламыз. А мен В нүктелерін центр ретінде қабылдап FG қашықтықта К нүктесінде қиылысатын дөңгелектер сызайық. К нүктесін центр ретінде қабылдап KА қашықтықта ABL дөңгелегін сызамыз. ABL доғасын тең сегіз бөлікке бөліп, олардың бөліну нүктелерін хордалармен қосайық. АВ³⁰ сызығында тең қабырғалы және тең бұрышты тоғыз бұрыш шығады. Міне оның суреті [56 - сурет].

                      

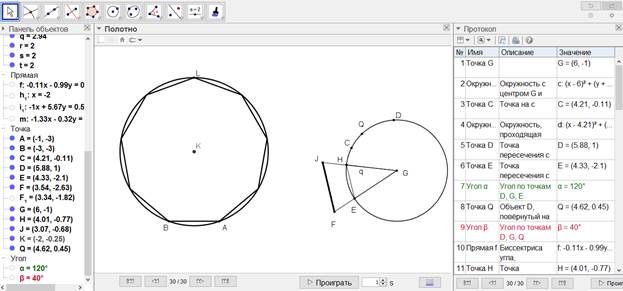
[56 - сурет]

Салудың алгоритмі:

1-қадам. Центрі G нүктесі етіп алып кезкелген w1 шеңберін сызамыз.

2-қадам. w1 шеңберінің бойынан C нүктесін белгілейміз.

3-қадам. C нүктесінен ұзындығы w1 шеңберінің радиусына тең CD және CE хордаларын жүргіземіз, яғни CD=R_w1, CE=R_w1.

4-қадам. CD доғасын тең үш бөлікке бөлетіндей, GK және GH сәулелерін жүргіземіз. 

5-қадам. GK және GE сәулелерін IF=AB болатындай етіп созамыз(18-сурет).

6-қадам. Центрлері A және B нүктелері, ал радиустары GI кесіндісіне тең болатын w2, w3 шеңберлерін сызып, олардың қыйылысу нүктесін O деп аламыз.

7-қадам. O нүктесін центрі етіп алып, радиусы OA кесіндісіне тең болатын w4 шеңберін сызамыз.

8-қадам. AB кесіндісінің ортасы арқылы өтетін перпендикуляр жүргізіп, оның w4 шеңберімен қыйылысу нүктесін L деп аламыз.

9-қадам. ALB доғасын теңдей сегіз бөлікке бөліп, оларды хордалармен қосамыз.

Математикалық негіздеме: Берілген алгоритмнің үшінші қадамы бойынша алынған CD және CE  кесінділері w1 шеңберінің радиусына тең болғандықтан CDG үшбұрышы мен GEG үшбұрышы тең қабырғалы үшбұрыштар. Ал, тең қабырғалы үшбұрыштың ішкі бұрыштары 60⁰ тең болатынын ескерсек, DE доғасы 120⁰-тық доға. Демек, бұл доға w1 шеңберінің үштен бір бөлігі. Төртінші қадам бойынша алынған KE кесіндісі w1 шеңберіне іштей сызылған дұрыс тоғызбұрыштың бір қабырғасы болып табылады, себебі KE доғасы DE  доғасының үштен бір бөлігі. IF кесіндісі KE кесіндісін параллел көшіру арқылы алынған бастапқы берілген кесіндіге тең кесінді болғандықтан, ол радиусы GI кесіндісіне тең болатын шеңберге іштей сызылған дұрыс тоғызбұрыштың қабырғасы болып табылады. Ал, шеңберді қандай да бір бөлікке бөліп тұрған доғаға сәйкес хорда сызылып тұрса, онда қабырғасының саны сол бөлік санына сәйкес дұрыс көпбұрыштың салынатынын ескерсек, берілген алгоритм бойынша салынға тоғызбұрышты дұрыс тоғызбұрыш деп атауға болады.

 

[X] Он бұрышты салу туралы. Егер ол АВ сызығына он бұрышты қалай тұрғызу керек десе, онда АВ сызығын С нүктесінде қақ бөліп В нүктесіне АВ сызығына тең ВD перпендикулярын орнатамыз. С нүктесін центр ретінде қабылдап АВ сызығында CD қашықтықта Е-ні белгілейміз. Ары қарай А мен В нүктелерінің әрқайсысынан центрлер ретінде АЕ қашықтықта G нүктесінде қиылысатын екі доға сызайық. G нүктесін қабырғасы АВ сызығы болып келген он бұрышқа  іштей сызылған дөңгелектің центрі ретінде қабылдаймыз. Ендеше, егер біз G центрі бар AG қашықтықта ABHF дөңгелегін сызып алып, AG мен GB сызықтарын олардың бағыттарында дөңгелектің шеңберіне дейін F пен H нүктелеріне дейін созсақ, АН пен BF доғаларын тең төрт бөлікке бөліп хордалармен қоссақ, онда тең қабырғалы және тең бұрышты он бұрышты аламыз³¹. Міне оның суреті [57 - сурет].

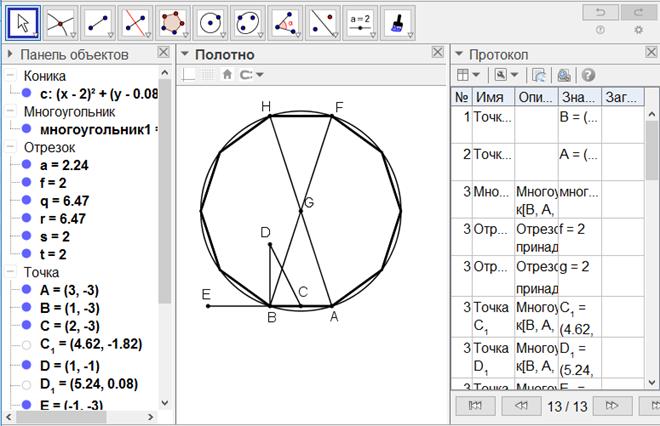
[57 - сурет]

Салудың алгоритмі: Егер ол АВ сызығына он бұрышты қалай тұрғызу керек десе, онда

1.     АВ сызығын С нүктесінде қақ бөлеміз

2.     В нүктесіне АВ сызығына тең ВD перпендикулярын орнатамыз.

3.     С нүктесін центр ретінде қабылдап АВ сызығында CD қашықтықта Е-ні белгілейміз.

4.     Ары қарай А мен В нүктелерінің әрқайсысынан центрлер ретінде АЕ қашықтықта G нүктесінде қиылысатын екі доға сызамыз.

5.     G нүктесін қабырғасы АВ сызығы болып келген он бұрышқа  іштей сызылған дөңгелектің центрі ретінде қабылдаймыз.

6.     Центрі G болатын AG қашықтықта ABHF дөңгелегін сызамыз

7.     AG мен GB сызықтарын олардың бағыттарында дөңгелектің шеңберіне дейін F пен H нүктелеріне дейін созамыз

8.     АН пен BF доғаларын тең төрт бөлікке бөліп хордалармен қоссақ, онда тең қабырғалы және тең бұрышты он бұрышты аламыз³¹.

Математикалық негіздеу:

Дұрыс онбұрышқа сырттай сызылған шеңбердің радиусы  екендігі белгілі. Ал, берілген алгоритм бойынша AB қабырғасын -ға тең деп алсақ,     Яғни, EA=R  болып табылады. Бізге дәлелдеу керегі де осы.

 

[ХІ] Егер ол АВ сызығына тең циркуль ашасымен ғана, АВ сызығына тең қабырғалы тең бұрышты он бұрышты тұрғызу керек десе, онда оған жоғарыда төртінші ұсыныста көрсетілгендей бесбұрыштың үшбұрышын тұрғызамыз. G нүктесі АВ сызығына қарсы жатқан бұрыштың [төбесі] болсын. A және G, B және G сызықтарын қосамыз. G нүктесін  центр ретінде қабылдап, АВ қашықтықта CDFH дөңгелегін сызайық. AG, BG сызықтарын олардың бағытында дөңгелектің шеңберіне дейін [F және C нүктелеріне дейін] созайық. HF және DC доғаларының әрқайсысын тең төрт бөлікке бөліп, FI, IK, KM, MH, CL, LN, NX, XD бөліктерін аламыз. GF, GI, GK, GM, [GL], GN, GX, [GC], GH сызықтарын жүргіземіз де CDH дөңгелегінің центрінен шығатын осы сызықтардың әрқайсысында AD сызығына тең сызықтарды қосамыз. Бұл соңында О тұрған сызықтар. Оларды өзара және А мен В нүктелерімен түзу сызықтармен қосайық. Тең қабырғалы тең бұрышты АВО³² шығады. Міне оның суреті [58 - сурет].

 

[58 - сурет]

 

Салудың алгоритмі: Егер ол АВ сызығына тең циркуль ашасымен ғана, АВ сызығына тең қабырғалы тең бұрышты он бұрышты тұрғызу керек десе, онда

1.     Жоғарыда төртінші ұсыныста көрсетілгендей бесбұрыштың үшбұрышын тұрғызамыз.

2.     G нүктесі АВ сызығына қарсы жатқан бұрыштың [төбесі] болсын деп алып, A және G, B және G сызықтарын қосамыз.

3.     G нүктесін центр ретінде қабылдап, АВ қашықтықта CDFH дөңгелегін сызамыз.

4.     AG, BG сызықтарын олардың бағытында дөңгелектің шеңберіне дейін [F және C нүктелеріне дейін] созамыз.

5.     HF және DC доғаларының әрқайсысын тең төрт бөлікке бөліп, FI, IK, KM, MH, CL, LN, NX, XD бөліктерін аламыз.

6.     GF, GI, GK, GM, [GL], GN, GX, [GC], GH сызықтарын жүргіземіз де CDH дөңгелегінің центрінен шығатын осы сызықтардың әрқайсысында AD сызығына тең сызықтарды қосамыз.

7.     Бұл соңында О тұрған сызықтар. Оларды өзара және А мен В нүктелерімен түзу сызықтармен қосамыз. Сонда тең қабырғалы тең бұрышты АВО³² шығады.

 

Математикалық негіздеу:

Бұл салуда да алдыңғы есепте қарастырғанымыздай дұрыс онбұрышқа сырттай сызылған шеңбердің радиусы  екендігіне сүйенеміз. Берілген алгоритм бойынша AB қабырғасын -ға тең деп алсақ,     Яғни, EA=R  болып табылады. Бізге дәлелдеу керегі де осы.