Салудың алгоритмі:

1.  AВС сегментін саламыз да В нүктесінде тең екіге бөлеміз.

2.  AВ және ВС нүктелерін қосамыз.

3.  А және С нүктелерінен ВСD ;және BAD  тік бұрышын тұрғызамыз,

4.  E нүктесі ABC шеңберінің центрі болып табылады.

Сонда E нүктесі ABC⁷ доғасының центрі болып табылады.

Математикалық негіздеу: Тікбұрышты үшбұрышқа сырттай сызылған шеңбердің центрі гипотенузаның  қақ ортасында жатады.

[II] Егер ол центрі D нүктесі болатын ВС дөңгелегіне А нүктесінен қалай жанама жүргізуге болады десе, онда AD сызығын жүргіземіз. Ол ВС дөңгелегін В нүктесінде қияды. D центрінен DА қашықтықта AE дөңгелегін салайық. В нүктесінде АВЕ тік бұрышын тұрғызып, ВС дөңгелегін С нүктесінде қиятын ЕD сызығын жүргіземіз. А мен С - ны қосамыз. Сонда АС ВС⁸ дөңгелегіне жүргізілген жанама болып табылады. Міне оның суреті [34 - сурет].

 

 

 

 

 

 

[34 - сурет]

Салудың алгоритмі:

1.     Центрі D нүктесі болатын ВС дөңгелегіне А нүктесінен жанама жүргізу үшін AD кесіндісін жүргіземіз.

2.      AD кесіндісі ВС дөңгелегін В нүктесінде қияды. D центрі арқылы радиусы AD болатындай AE дөңгелегін сызамыз.

3.     В нүктесі арқылы АВЕ тік бұрышын тұрғызып, ВС дөңгелегін С нүктесі арқылы кесетін ЕD кесіндісін жүргіземіз.

4.      А және С нүктелерін қосамыз.

Сонда АС кесіндісі ВС дөңгелегіне жүргізілген жанама болады.

Математикалық негіздеу: Шеңберге жүргізілген жанама радиусқа перпендикуляр болады.

 

[IIІ] Егер ол жанаманы қолөнершінің тәсілі бойынша сал десе, онда сызғышты ВС сызығына орналастырып циркульді бір шамаға ашамыз. Егер оның бір ұшы сызғыш бойымен қозғалатын болса, онда екінші ұшы А нүктесі арқылы өтіп, ВС⁹-ға параллель сызықты береді. Міне оның суреті [35 - сурет].

 

 

 

 

 

 

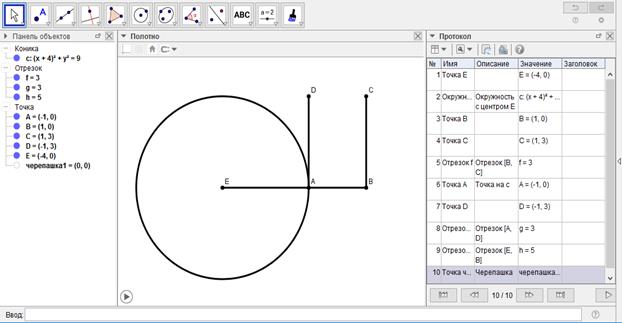
[35 - сурет]

Салудың алгоритмі:

Қолөнерші (ремесленник) әдісімен салсақ

1.  Е нүктесінен шеңберді А нүктесінде қиятын ВС кесіндісіне перпендикульяр ЕВ кесіндісін сызамыз.

2.  Циркульді АВ кесіндісіне тең болатындай ашып бір басын ВС кесіндісіне қоямыз

3.  Бір басы ВС кесіндісінің бойымен жылжитындай циркульдің екі басын бірдей жылжытамыз.

Сонда АD кесіндісі дөңгелекке жүргізілген жанама болады.

Математикалық негіздеу: ЕВС=90, AD кесіндісі АВ парраллель болғандықтан ЕАD=90.  Шеңберге жүргізілген жанама радиусқа перпендикуляр болады

 

[IV] Егер ол: А нүктесінен ABC дөңгелегінің шеңберіне жанаманы қалай жүргізеді десе, онда А нүктесін дөңгелектің центрі D нүктесімен қосамыз, демек А мен D-ны [AD сызығымен] қосамыз. А нүктесінде AD сызығының бойымен DAE тікбұрышын тұрғызамыз. Сонда АЕ сызығы ABC дөңгелегіне жанама болады¹⁰. Міне оның суреті [36 - сурет].

 

 

 

 

 

[36 - сурет]

Салудың алгоритмі:

1.     А нүктесімен дөңгелектің D центрін қосамыз.

2.     А нүктесінен өтетін DAE тік бұрышын тұрғызамыз.

Сонда АD кесіндісі дөңгелекке жүргізілген жанама болады.

Математикалық негіздеу: Шеңберге жүргізілген жанама радиусқа перпендикуляр болады

 

[V] Егер ол АВС үшбұрышының АВ және АС сызықтарының арасына ВС-ға параллель болатын және егер ВС сызығы D сызығынан кіші болған жағдайда берілген D сызығына тең сызық сал десе, онда ВС сызығын оның бағытында [ВЕ D-ға тең болатындай Е нүктесіне дейін] созып, ал [егер ВС D сызығынан үлкен болса] D-ға тең ВЕ сызығын ВС сызығына саламыз. Е нүктесінен АВ сызығына параллель сызық жүргіземіз. Ол АС-ны G нүктесінде қиып өтеді. G нүктесінен ВС сызығына параллель сызық жүргіземіз; Бұл АВ-мен қиылысатын GH сызығы. Сонда GH D сызығана тең және ВС¹¹ сызығына параллель.  Міне оның суреті [37 - сурет].

 

 

 

 

 

 

 

[37 - сурет]

Салудың алгоритмі:

1.     Егер ВС<D болса онда, ВС қабырғасын ВЕ=D болатындай Е нүктесіне дейін созамыз.

2.     Егер ВС>D болса онда, ВС қабырғасын ВЕ=D болатындай Е нүктесін белгілейміз.

3.     Е нүктесінен АВ қабырғасына параллель болатын ЕH кесіндісін саламыз.

4.     G нүктесінен CВ қабырғасына параллель болатын GH кесіндісін саламыз.

5.     Сонда GH=D болады.

Сонда HG BC қабырғасына параллель және HG=D кесіндісіне тең болады.

Математикалық негіздеу: Салу алгоритмінің өзі дәлелдеп тұр.

 

[VI] Егер ол АВС үшбұрышының АВ және АС сызықтарының арасына ВС сызығына параллель, мысалы АВ сызығында ол қиып алатын кесіндіге тең, яғни ЕВ сызығына тең DE сызығын салу керек болса, онда АСВ бұрышын BD сызығымен қақ бөлеміз де, D нүктесінен ВС-ға параллель DE сызығын жүргіземіз. Сонда DE сызығы ЕВ¹² сызығына тең. Міне оның суреті [38 - сурет].

 

 

 

 

 

[38 - сурет]

Салудың алгоритмі:

1.     АВС бұрышын тең екіге бөлетіндей DE түзуін жүргіземіз.

2.     АС қабырғасында жататын D нүктесі арқылы ВС-ға параллель DЕ кесіндісін жүргіземіз.

3.     Сонда DE=EB болады.

Сонда DЕ ВС қабырғасына параллель және ЕВ және F кесіндісіне тең болады.

Математикалық негіздеу: CBD=ABD және СВDE болғандықтын,CBD=BDE, демек BDЕ=DВЕ, яғни BDE үшбұрышы тең бүйірлі болғандықтын DE=EB болады.

 

 [VII] Егер ол АВС үшбұрышында, мысалы, ВС сызығына параллель және ВЕ мен F сызықтарына тең DE сызығын сал десе, онда ВС сызығына  F сызығына тең BG сызығын салып, G нүктесі арқылы АВ-ға параллель GH сызығын жүргізіп, HGC бұрышын қақ бөлетін GD сызығын [G нүктесі арқылы] жүргіземіз де D нүктесінен ВС сызығына параллель DE сызығын жүргіземіз. Сонда DE сызығы  ВЕ және F¹³ сызықтарына тең. Міне оның суреті [39 - сурет].

 

 

 

 

 

[39 - сурет]

Салудың алгоритмі:

1.     ВС қабырғасынын F кесіндісіне тең болатындай ВG кесіндісін белгілейміз.

2.     G нүктесінен АВ қабырғасына параллель болатын GH кесіндісін саламыз.

3.     HGC бұрышын қақ бөлетіндей GD кесіндісінін саламыз.

4.     D нүктесінен ВС қабырғасына параллель болатындай DЕ кесіндісін сызамыз.

Сонда DЕ ВС қабырғасына параллель және ЕВ және F кесіндісіне тең болады.

Математикалық негіздеу: Бұл есепте әл-Фараби жазбаларын аударғанда қате кетуі мүмкін. Салу алгоритмінің 4- қадамында DE сызығының орнына KE болған жағдайда  салу дұрыс болады.

 

[VIII] Басқа үшбұрышқа тең үшбұрышты салу туралы.  Егер ол қабырғалары басқа үшбұрыштың қабырғалырына тең үшбұрышты сал десе [мысалы АВС], онда DE түзу сызығын жүргіземіз де, АВ сызығына тең DG,  BC сызығына тең GH және СА тең HF сызығын  саламыз. G нүктесін центр ретінде қабылдап GD қашықтығында дөңгелек бөлігін келтірейік, сол сияқты H нүктесін центр ретінде қабылдап HF қашықтығында дөңгелек бөлігін келтіреміз. Бірінші бөлігі [екінші бөлігін] I нүктесінде қиып өтеді. Ары қарай GI және ІH сызықтарын жүргізейік. Онда GIH үшбұрышының қабырғалары АВС¹⁴ үшбұрышының қабырғаларына тең. Міне оның суреті [40 - сурет].

 

 

 

 

 

 [40 - сурет]

Салудың алгоритмі:

1.  DE түзуін сызып, оның бойынан DG=АВ, GH=BC, HF=CA болатындай DG,GH,HF кесінділерін белгілейміз.

2.  Центрі G болатындай r=GD жартышеңберін саламыз.

3.  Центрі H болатындайr=HF жартышеңберін саламыз. Екі жартышеңбер I нүктесінде қилысады.

4.  GI және IHтүзулерін жүргіземіз.

Сонда GIH үшбұрышы ABC үшбұрышына тең болады.

Математикалық негіздеу: Үшбұрыштар теңдігінің бірінші белгісі.

 

[IХ] Бұрышты тең үш бөлікке бөлу туралы. Егер ол АВС бұрышын тең үш бөлікке бөл десе, онда АВС бұрышы тік бұрышты болса, ВС сызығында тең қабырғалы DBC үшбұрышын тұрғызамыз. Сонда ABD бұрышы тік бұрыштың үштен бір бөлігі. DBC бұрышын қақ бөлеміз¹⁵.  Міне оның суреті [41 - сурет].

 

 

 

 

 

[41 - сурет]

Салудың алгоритмі:

1.  DС түзуіне тең қабырғалы DBC үшбұрышын тұрғызамыз.Сонда ABD бұрышы ABC бұрышының үштен біріне тең болады.

2.  DBC бұрышын қақ бөлеміз.

Сонда ABC бұрышы тең үшке бөлінеді.

Математикалық негіздеу: 90-60=30, 60:2=30

 

 [Х] Егер бұрыш тік бұрыштан кіші болса, онда В нүктесін центр ретінде қабылдап, ВА қашықтықта DAС дөңгелегін келтіреміз. BD ны ВС-ға тік бұрыш бойынша қойып, СВ-ны дөңгелекпен қиылысқанша Е нүктесіне созамыз. Сызғышты А нүктесіне әкеліп, оны CDE дөңгелегінің шеңбері бойынша DB перпендикуляры және DE доғасының арасында жатқан HF сызығы DB сызығына тең болғанша қозғайтын боламыз, бұл жағдайда сызғыш А нүктесінен таймайды. Ары қарай EF доғасына тең EK доғасын саламыз да, KB жүргізіп L нүктесіне дейінгі бағытта жалғаймыз. Онда LBC бұрышы АВС бұрышының үштен бірі болады. Әрі қарай ABL бұрышын қақ бөлеміз¹⁶. Міне оның суреті [42 - сурет].

 

 

 

 

 

[42 - сурет]

Салудың алгоритмі:

1.  В нүктесін центр етіп алып ВА қашықтықпен DAC шеңберін сызамыз.

2.  Сызғышты А нүктесіне қойып, BCВD жүргіземіз.

3.  ВС түзуін шеңбермен Е нүктесінде қилысқанға дейін созамыз.

4.       Сызғыштың бір басын А нүктесіне қойып, екінші басын CDE шеңбері бойымен DB және DE перпендикульярларының арасында жататын HF =DB болғанға дейін жылжытамыз.

5.       EF доғасына тең EK доғасын тұрғызамыз.

6.       KB түзуін L нүктесіне дейін созамыз.

Сонда LBC бұрышы ABC бұрышының үштен біріне тең болады.

Математикалық негіздеу:

 

[ХІ] Бұрышты тең үшке бөлудің басқа тәсілі.  АВС сүйір бұрышын тұрғызайық та және егер біз оны тең үш бөлікке бөлгіміз келсе, А нүктесінен ВС сызығына AD параллелін және  А нүктесінен ВС сызығына AH перпендикулярын түсіреміз. В нүктесіне сызғышты әкеліп, AD мен AH сызықтарының арасына орналасқан сызық екі еселенген АВ болғанша қозғайтын боламыз. Бұл мысалы DEB сызығы, демек DE сызығы екі еселенген АВ сызығы болып табылады. Ендеше DBC бұрышы АВС¹⁷ бұрышының үштен бір бөлігі. Міне оның суреті [43 - сурет].

 

 

 

 

 

[43 - сурет]

 

Салудың алгоритмі: АВС сүйір бұрышын теңдей үшке бөлу керек болса, онда

1.  А нүктесінен AHВC болатындай АН жүргіземіз.

2.  ВС параллель болатындай AD түзуін жүргіземіз.

3.  Сызғыштың бір басын В нүктесіне қойып, екінші басын ВD=2*AB болатындай BD түзуін жүргіземіз.

Сонда DBC бұрышы ABC бұрышының үштен біріне тең болады.

Математикалық негіздеу:

 

[ХІІ] Доғаны тең үш бөлікке бөлу туралы. Егер ол ABD доғасын тең үш бөлікке бөлу керек десе, онда осы доға орналасқан дөңгелектің центрін табамыз. Бұл Е нүктесі болсын. А мен Е-ні, Е мен D-ны қосып, ABCD доғасын В мен С нүктелерінде қиып өтетін ЕВ және ЕС сызықтарымен AED бұрышын үш тең бөлікке бөлеміз. Сонда ABCD доғасы үш тең бөлікке АВ, ВС және СD¹⁸ доғаларына бөлінетін болады. Міне оның суреті [44 - сурет].

 

 

 

 

 

[44 - сурет]

 

 

 

Салудың алгоритмі: АВС доғасын теңдей үшке бөлу керек болса, онда

1.  Доға орналасқан шеңбердің центрін тауып оны Е деп белгілейміз.

2.  AE және ED нүктелерін қосамыз.

3.  AED бұрышын теңдей үшке бөлеміз де, доғамен қилысу нүктелерін В және  С деп белгілейміз.

Сонда ABC[D] доғасы AB, BC және CD болып тең үшке бөлінеді.

Математикалық негіздеу: AED бұрышын теңдей үшке бөлгендіктен доға да тең үшке бөлінеді.

 

[ХІІІ] Екі еселенген басқа үйге немесе шарға тең немесе басқа қатынаста алынған үй немесе шар салу туралы. Егер ол ұзындығы, ені, биіктігі өзара тең екі еселенген басқа үй болып табылатын квадрат үйді салу керек болса немесе басқа екі еселенген болып келген шарды салу, немесе қақ бөліп немесе басқа бір қатынастарда болып табылатын шарды қалай салу керек десе, онда үй ұзындығына және шар диаметріне тең АВ сызығын тұрғызамыз, екі еселенген  тік бұрыш бойынша АВ сызығына АС сызығын салып, DABC жазық фигурасын толықтырамыз. AD мен ВС диагоналдарын жүргіземіз. Олар F нүктесінде қақ бөлінеді. Олардың бағытында DC мен DB сызықтарын созамыз. Cызғыштың шетін А нүктесіне қоямыз да оны GC және EB  сызықтары бойынша [ол оларды Е және G нүктелерінде қиылысқанша] GF пен FE тең болатындай болғанша қозғайтын боламыз.  Сонда үйдің ұзындығы немесе шардың диаметрі ВЕ¹⁹ сызығы болады.  Міне оның суреті [45 - сурет].

 

 

 

 

 

[45 - сурет]

 

Салудың алгоритмі: Берілген үйден екі есе, болмаса бірнеше есе үлкен биіктігі, ені және ұзындығы бірдей шаршы түрде үй немесе берілген шардан еселенген шарды немесе қақ бөлінген, болмаса басқа өлшемдегі шар салу керек болса, онда

1.  Шардың диаметріне немесе үйдің ұзындығына тең АВ кесіндісін саламыз.

2.  AВ-дан екі есе ұзын болатындай АС кесіндісін АВ-ға тік бұрышпен салып, пайда болған  фигураны DABC фигурасына толықтырамыз.

3.  AD және ВС диагональдарын жүргіземіз, олар F нүктесінде қилысады.

4.  DC және DB сызықтарын өз бағыттарымен созамыз.

5.  Сызғыштың қырын А төбесіне қоямыз да, GC және EB сызықтарының бойымен GF=FE (E және G нүктелерінде қияды деп есептейміз) болғанға дейін жылжытамыз.

Сонда үйдің ұзындығы немесе шардың диаметрі ЕВ болып табылады.

Математикалық негіздеу: Берілген бастапқы үйдің қабырғасын, немесе шардың радиусын a деп белгілесек, онда ол үйдің ауданы S=a², ал шардың ауданы S=pi*r² болатын еді, ал екі еселенген үйдің ауданы S_ү=2a² немесе екі еселенген шардың ауданы S=2pi*r² болуы керек. Яғни ЕВ=AB√2 болуы керек.

 

 

 

[ХІV] Өртегіш айна жасау туралы. Егер біз күн сәулелерінің көмегімен бір қашықтықтан затты өртейтін айнаны жасағымыз келсе, онда алдымен айнаны айқындайтын (лекало) даяр үлгісін жасайық. Ол үшін  дөңгелек салайық, оның жарты диаметрі өртегіміз келетін заттың арақашықтығының шамасына тең. Бұл АВС дөңгелегі болсын. Оның ADC диаметрін жүргізейік. DC сызығына С  нүктесінен бірнеше тең кесінділер салайық. Бұл кесінділер кіші болған сайын даяр үлгі жақсырақ және дәл болады. Бұл кесінділер CF, FH, HG, GE және ED болсын. D нүктесі арқылы [CD-ға] тік бұрыш бойынша E, G, H және F сызықтарын жүргізейік те, оларды екі жағына да B, I, K, L және М нүктелеріне дейін созайық. C мен В, С мен I, С мен K, С мен L, С мен М нүктелерін қосайық. CM сызығына тең FN сызығын, CL-ге тең HX, CK-ға тең GO, CI-ге тең EP және СВ-ға тең DS сызығын салайық. C, N, X, O, P және S нүктелерін қосайық та, осы сызық бойынша даяр үлгісін (лекало) жасайық. Сосын металдан, мысалы темірден, қоладан, мыстан немесе цинктен айна дайындайық та,  егер мүмкін болса, оны ысып жалтыратайық. Егер айна қисық болып шықса, оны даяр үлгісі бойынша даяр үлгіні айнаға С нүктесі даяр үлгінің ортасына дәл келетіндей айнаның даяр үлгімен беттесуіне қол жеткізетіндей етіп даяр үлгіні айнаға беттестіріп түзетеміз. Сонда үлкен өртегіш күші²⁰ бар өртегіш айнаны аламыз. Міне оның суреті [46 - сурет].

 

 

 

 

 

[46 - сурет]

 

Салудың алгоритмі: Егер күн сәулесі арқылы алыстағы затты жандыратын айна салу керек болса, онда алдымен айнаның қалыбын (лекало) жасап алу керек. Ол үшін

1.       Жарты диаметрі біз жағатын заттың қашықтығына тең болатындай шеңбер тұрғызамыз. Бұл шеңберді АВС деп алайық.

2.       AСD диаметрін жүргіземіз.

3.       DC түзуінің бойынан С нүктесінен бірдей бірнеше кесінділер сызамыз.

4.       Бұл кесінділер неғұрлым қысқа болған сайын қалыбымыз (лекало) соғұрлым дәл болады. Бұл кесінділерді CF, FH, HG, GE, ED деп алайық.

5.       D нүктесі арқылы өтетін, CD  түзуіне перпендикульяр E,G,H,F түзулерін екі бағытқа қарай B,I,K,L,M нүктелеріне дейін созамыз.

6.       C және B, C және I, C және K, C және L, C және M нүктелерін қосамыз.

7.       CM-ге тең FN, CL-ге тең HX, CK-ге тең GO, CI-ге тең EP, CB-ге тең DS түзулерін жүргіземіз.

8.       C,N,X,O,P және S нүктелерін қосып, осы сызықтар негізінде қалыпты жасаймыз.

9.       Содан соң айнаны металлдан жасаймыз. Мысалы темірден, болаттан, мыстан немесе цинктан жасаймыз, мүмкін болса барынша жалтыратамыз.

10.   Егер айна қисық болса, онда С нүктесін қалыптың ортасына келетіндей етіп айнаны түзетеміз. 

Сонда үлкен күші бар жандырғыш айна жасалады.

Математикалық негіздеу: CMF және   CNU үшбұрыштары ұқсас. CD=a, CF=x деп белгілесек  

 

 

 

[ХV] Өртегіш айна жасаудың екінші тәсілі.  Егер оны біз жасағымыз келсе, онда кез келген қашықтықты [оның жартысы АВ сызығы болсын] аламыз да, оны С нүктесіне дейінгі оның бағытына созамыз. В нүктесіне ВС-ға перпендикуляр DB сызығын қарама-қарсы екі жағына да орнатайық та, ВС сызығына өзара тең кіші сызықтарды BE, EG, GH және HC салайық. F нүктесінде АЕ-ні қақ бөліп, F центрінен FA  қашықтықта дөңгелек сызайық. Ол BD сызығын I нүктелерінде қияды. I нүктелерінен AC сызықтарына параллель IL сызықтарын жүргізейік те  Е нүктесінен BD сызығына параллель сызықты L нүктелеріне дейін жүргізейік. Сосын AG сызығын М нүктесінде қақ бөліп, М нүктесінен  МА қашықтықта дөңгелек сызамыз. Ол BD сызығын N нүктелерінде қияды. N нүктелерінен АС сызығына параллель NX сызықтарын Х нүктесіне дейін жүргіземіз. Сосын АН сызығын О нүктесінде қақ бөліп, О центрінен ОА қашықтықта дөңгелек сызамыз. Ол BD сызығын Р нүктелерінде қияды. Р нүктелерінен ВС-ға параллель Z нүктелеріне дейін сызықтар жүргізейік. B, L, X және Z нүктелерін сызықпен қосып, даяр үлгі аламыз. Егер біз даяр үлгіні тексеретін болсақ, оны В нүктесін айнаның ортасына орналастырамыз. Сонымен біз үлкен өртегіш күші бар өртегіш айна аламыз²¹.  Міне оның суреті [47 - сурет].

 

 

 

 

 

[47 - сурет]

 

Салудың алгоритмі: Егер күн сәулесі арқылы алыстағы затты жандыратын айна салу керек болса, онда

1.       Жартысы АВ –ға тең болатындай кез-келген қашықтықтағы Жарты диаметрі біз жағатын заттың қашықтығына тең болатындай шеңбер тұрғызамыз. Бұл шеңберді АВС деп алайық.

2.       AСD диаметрін жүргіземіз.

3.       DC түзуінің бойынан С нүктесінен бірдей бірнеше кесінділер сызамыз.

4.       Бұл кесінділер неғұрлым қысқа болған сайын қалыбымыз (лекало) соғұрлұм дәл болады. Бұл кесінділерді CF, FH, HG, GE, ED деп алайық.

5.       D нүктесі арқылы өтетін, CD  түзуіне перпендикульяр E,G,H,F түзулерін екі бағытқа қарай B,I,K,L,M нүктелеріне дейін созамыз.

6.       C және B, C және I, C және K, C және L, C және M нүктелерін қосамыз.

7.       -CM-ге тең FN, CL-ге тең HX, CK-ге тең GO, CI-ге тең EP, CB-ге тең DS түзулерін жүргіземіз.

8.       C,N,X,O,P және S нүктелерін қосып, осы сызықтар негізінде қалыпты жасаймыз.

9.       Содан соң айнаны металлдан жасаймыз. Мысалы темірден, болаттан, мыстан немесе цинктан жасаймыз, мүмкін болса барынша жалтыратамыз.

10.   Егер айна қисық болса, онда С нүктесін қалыптың ортасына келетіндей етіп айнаны түзетеміз. 

Сонда үлкен күші бар жандырғыш айна жасалады.

 

Математикалық негіздеу: Бұл есептің дәлелдеуі де алдыңғы есеппен ұқысас.