Салу алгоритмі: әл Фәрәби әдісі бойынша салу (2-сурет):

1) берілген сфераның бетінде жатқан нүктелер арқылы өтетін кез келген ABG шеңберін жүргіземіз, оның центрін С деп белгілейміз. ABG шеңберін оңың бойында жатқан А мен В нүктелерінде қақ бөлеміз.

2) А, С, В және D нүктелері арқылы өтетін сфераның диаметрлік қимасын саламыз. Ол үшін:

а) С нүктесі арқылы ABG дөңгелегінің жазықтығына  DE перпендикулярын тұрғызамыз;

 арқылы дөңгелек саламыз; мұндағы  – нүктелері берілген сфераға тиісті;

б) ;

в) Шеңбер  –  ізделінді үлкен шеңбер (диаметрлік қима).

Математикалық негіздеу: салуымыз бойынша алынған кесінділерді  деп белгілейік. Сонда қиылысатын хордалардың қасиеті бойынша:  немесе  ендеше:   AC кесіндісі – DC және CE кесінділерінің геометриялық (пропорционалдық) ортасы екендігі шығады. Бұдан AC кесіндісі –  тікбұрышты үшбұрышының А тік бұрышынан түсірілген биіктік, деп тұжырымдауға болады. Ал,  DC және CE кесінділері  – DA және AE катеттерінің DE гипотенузасындағы проекциялары. Ендеше, іштей сызылған  бұрышы – тік бұрышты, олай болса, ол диаметрге тіреледі. Бұдан DE хордасы – берілген сфераның диаметрі болып табылады. Ал, осы диаметр арқылы жүргізілген дөңгелек берілген сферамен шектелген шардың ізделінді диаметрлік қимасы, ал оның шеңбері  сфераның ізделінді үлкен шеңбері болып табылады. Дәлелдеу керегі осы.

 

 

 

 

 

 

 

 

 

 

 

 

 

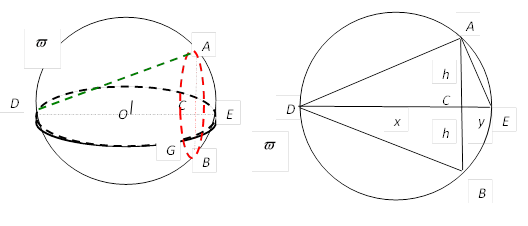
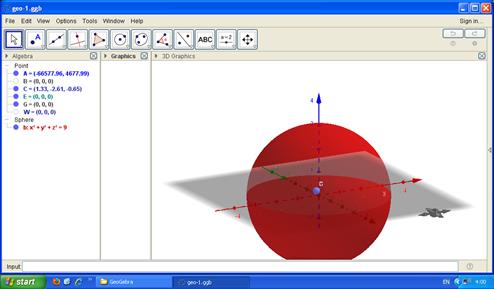
2-сурет. Трактаттағы № 154 сурет бойынша сызбалар

 

Зерттеу: бастапқы кез келген нүктелерді сфераның бойынан қалауымызша алғандықтан, есептің шексіз көп шешімі болады.

 

[II] Егер ол сферада тік бұрышпен қиылысатын екі үлкен дөңгелекті қалай жүргізуге болады десе,  онда сферада үлкен дөңгелек жүргіземіз, мысалы, ABCD дөңгелегі, және оны A, B, C, D нүктелері арқылы тең төрт бөлікке бөлеміз. Ары қарай А нүктесін полюс ретінде қабылдап,  [А-дан] B және D ара қашықтығында  дөңгелек саламыз. Бұл BED  дөңгелегі болады. ABCD және  BED екі үлкен дөңгелек тік бұрыш арқылы қиылысады. Міне оның суреті [169-сурет].

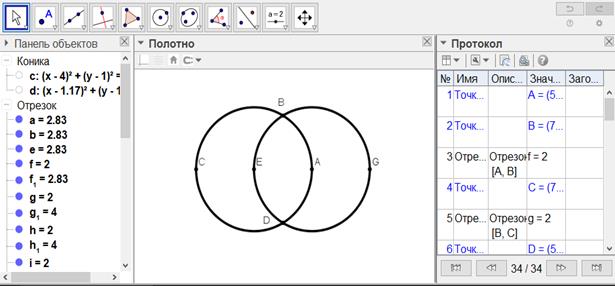
[169-сурет]

Есептің шешуі

Салу керек: сфераның өзара перпендикуляр болатын екі үлкен шеңбері.

Салу: әл Фәрәби әдісі бойынша салу (4-сурет):

1) Сферамен шектелген шардың ABCD үлкен дөңгелегін саламыз;

2) ABCD дөңгелегін А, В, С, D нүктелерінде тең төрт бөліктерге бөлеміз;

3) А нүктесін центр етіп алып, А-дан В және D нүктелеріне дейінгі қашықтықтарда BEDG шеңберін жүргіземіз: Шеңбер (A; r=AB=AD-AE=AG) және .

 

 

 

 

 

 

 

 

 

 

 

 

 

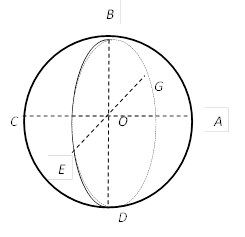
4-сурет. Трактаттағы № 155 сурет бойынша сызба

 

4) ABCD және BEDG – ізделінді екі үлкен шеңберлер тікбұрыш жасап қиылысады.

Математикалық негіздеу: салуымыз бойынша қима жазықтықтар сфераның перпендикуляр диаметрлері арқылы өтеді. Бұдан осы қимамен шекттелген және сфераның ортақ нүктелерімен шектелген диаметрлік екі шеңберлер де перпендикуляр болатындығы шығады. Дәлелдеу керегі осы.

 

[III] Егер ол сферада тік бұрышпен қиылысатын үш үлкен дөңгелек жүргіземіз десе, онда бұрынғыдай А және С нүктелерінде тік бұрышпен қиылысатын екі үлкен дөңгелек саламыз. Бұл тік бұрышпен қиылысатын ABCD және  BEDG дөңгелектері. Ары қарай   BCD доғасын С нүктесінде қақ бөлеміз, В нүктесін полюс етіп алып ВС қашықтықта СЕAG  дөңгелегін саламыз. Сонда бір - бірімен тік бұрышпен59  қиылысатын  ABCD, BEDG және CEAG үш дөңгелегін аламыз. Міне оның суреті [170-сурет].

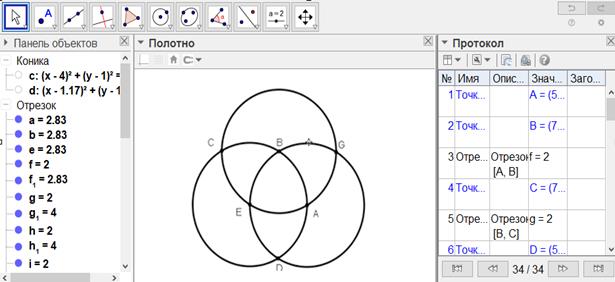
[170-сурет]

Есептің шешуі

Салу керек: сфераның өзара перпендикуляр болатын үш үлкен шеңберлері (диаметрлік қималары).

Салу: әл Фәрәби әдісі бойынша салу (6-сурет):

1) Сфераның А және С нүктелерінен өтетін өзара перпендикуляр болатын екі диаметрлік қималарын саламыз (ІІ-есеп). Бұл өзара тікбұрыш жасап қиылысатын ABCD және BEDG  шеңберлері;

2) С нүктесінде BСD доғасын қақ бөлеміз, сондай-ақ, В нүктесін центр, ал ВС-ны радиус етеп алып, СЕAG дөңгелегін саламыз. Бұл Шеңбер3 (В, r3=BC=BE=BA=BG)-пен шектелген дөңгелек.

3) Сонда, өзара тікбұрыш жасап қиылысатын ABCD, BEDG және CEAG, үш диаметрлік қималар аламыз: ABCD BEDG CEAG – сфераның ізделінді үлкен шеңберлері (диаметрлік қималары).

Математикалық негіздеу: салуымыз бойынша, үшінші жазықтық – екінші есепте салу жолы дәлелденген екі перпендикуляр дөңгелектердің сызықтық бұрышының қабырғалары арқылы өтеді.  Ендеше бұлар сферамен шектелген шардың өзара перпендикуляр болатын үш диаметрлік қималары болып табылады. Дәлелдеу керегі осы.

 

 

 

 

 

 

 

 

 

 

 

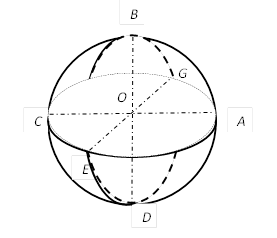
6-сурет. Трактаттағы № 156 сурет бойынша сызба

 

 

  [IV] Егер ол сфераның екі нүктесі арқылы өтетін үлкен   дөңгелекті  қалай жүргізуге болады десе, онда осы нүктелердің әрбірін [бұл А және В нүктелері болсын]  полюс ретінде қабылдап үлкен дөңгелектің төрттен біріндей қашықтықта CDEB және CGEA дөңгелектерін саламыз.   Бұл дөңгелектер  С және Е нүктелерінде қиылысады. Әрі қарай бұл дөңгелектердің қиылысу орнын полюс ретінде қабылдаймыз және {осыдан} {берілген} нүктеге дейінгі қашықтықта дөңгелек тұрғызамыз, бұл үлкен дөңгелек болып саналатын АВН болсын. Міне оның суреті [171-сурет].

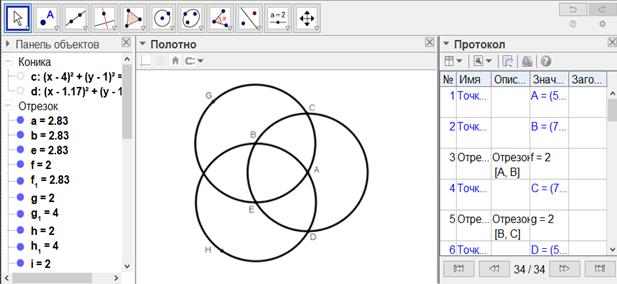
[171-сурет]

Есептің шешуі

Салу керек: сфераға тиісті екі нүкте арқылы өтетін үлкен шеңбер.

Салу: әл Фәрәби әдісі бойынша салу (8-сурет):

1) осы нүктелердің әрқайсысын центр етіп алып (айталық, бұл нүктелер А және В нүктелері болсын), радиусы үлкен дөңгелектің төрттен бірі болатын қашықтықта CDEB және  CGEA дөңгелектерін саламыз: Шеңбер1  және Шеңбер2 , мұндағы d=HK – сфераның диаметрі;

2) Бұл шеңберлермен шектелген шарлар С және Е нүктелерінде қиылысады: Дөңгелек1 Дөңгелек2 = CE;

3) CE-нің ортасынан CAE немесе CEB дөңгелектерінің жазықтығына HK перпендикулярын тұрғызамыз;

4) HK-ның ортасын O центр, одан берілген нүктелерге дейінгі қашықтықты радиус деп алып, шеңбер жүргіземіз: О | , OH=OK және OС=OE: Шеңбер3 (O, r3=OH=OA=OB=OK) | A, B, H Шеңбер3;

5) Бұл шеңбермен шектелген АВН дөңгелегі – ізделінді диаметрлік дөңгелек, ал АВН шеңбері – ізделінді үлкен шеңбер болып табылады

 

 

 

 

 

 

 

 

 

8-сурет. Трактаттағы № 157 сурет бойынша сызба

 

Математикалық негіздеу: салуымыз бойынша келесі хордалар мен дөңгелектер өзара перпендикуляр:  және  HK хордасы CE хордасын қақ бөледі, сонымен бірге A және B нүктелері CE кесіндісі арқылы қиылысатын дөңгелек жазықтықтарына тиісті, есептің шарты бойынша, бұл нүктелер сфераға да тиісті, ендеше, осы шеңбермен шектелген дөңгелек шардың диаметрлік қимасы болып табылады, мұндағы:  A, B, H Шеңбер3  – сфераның үлкен шеңбері (диаметрлік қима). Дәлелдеу керегі осы.

Ескертпе: әл Фәрәбидің «Рухани айлалы тәсілдер мен геометриялық фигуралардың табиғи сырлары туралы» кітабына А. Көбесовтың түсініктемелеріндегі № 59  ескертпе [1, б.: 230.]: Сфераға іштей сызылған дұрыс октаэдр салумен барабар  (Евклидтің «Бастамасындағы» XIII  кітаптың 14 сөйлемі (т. III, бет.: 124-125)) [2, б.: 124-125].

Салу керек: сфераға іштей сызылған дұрыс октаэдр салу.

Салу: Евклид әдісі бойынша салу (9,10-суреттер):

1) AB-ға тең кесінді өлшеп саламыз;

2) оны С нүктесінде қақ бөлеміз;

3) AB кесіндісін диаметрі етіп, ADB жартышеңберін жүргіземіз;

4) C нүктесінен  AB –ға  перпендикуляр CD кесіндісін саламыз, мұндағы ;

5) DB кесіндісін саламыз;

6) Әр қабырғасы DB-ға тең EIHG квадратын қарастырамыз;

7) GI, EH жүргіземіз;

8) K нүктесінен EIGH квадратының жазықтығына KLперпендикулярын тұрғызамыз;

9) оны EIGH квадратының жазықтығына екінші жағына созамыз, созындыны KM деп, белгілейміз.

10) KL және KM түзілерінен KL және KM кесінділерін қиып аламыз, олар EK, IK HK, GK кесінділеріне тең;

11) LE, LI, LH, LG, ME, ML, MH, MG кесінділерін саламыз (9-сурет);

12) LE, LI, LH, LG, ME, MІ, MH, MG кесінділері іштей сызылған дұрыс октаэдрдің қабырғалары. Осы октаэдр – Евклид есебіндегі ізделінді фигура.

Ал, әл Фәрәбидің IV-есебіне А. Көбесовтың көрсеткен Евклид әдісі бойынша салуда: LM=A B(10-сурет)  – сфераның диаметрі және олар арқылы өтетін дөңгелектің шеңбері – ізделінді үлкен шеңбер болып табылады.

 

 

 

 

 

 

 

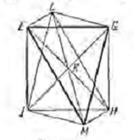
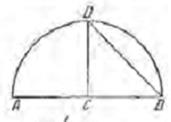
9-сурет. Евклидтің «Бастамасындағы» XIII  кітаптың 14 сөйлеміндегі сызба

 

 

 

 

 

 

 

 

 

 

 

 

 

 

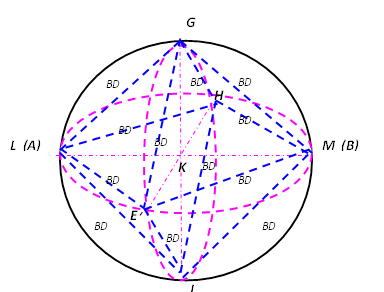
10-сурет. Трактаттағы № 157 сурет бойынша сызба

 

Математикалық негіздеу: диаметрлік қимаға іштей сызылған EIHG және LEMH квадраттары өзара тең, ендеше, олардың қабырғалары тең. Салуымыз бойынша бұл кесінділер BD-ға тең және сфераға іштей сызылған октаэдр құрайды. Сфераның диаметрі берілген A және B нүктелері арқылы өтеді.  Дәлелдеу керегі осы.

 

[V] Тең қабырғалы үшбұрыш болатындай  сфераны теңдей төрт бөлікке бөлу туралы. Егер ол тең қабырғалы және тең бүйірлі үшбұрыш болатындай  сфераны қалай теңдей төрт бөлікке бөлу керек десе, онда үш дөңгелек жүргіземіз: бұл дөңгелектер ABCD, BEDG  және CEAG. Сонда сфераны теңдей сегіз үшбұрышқа бөлеміз; бұл үшбұрыштар ABE, AED, ADG, AGB, CBE, CED, CDG және CGB. Үшбұрыштардың біреуінің центрі және осы үшбұрыштың әр бұрышы арқылы үлкен дөңгелектер доғаларын жүргіземіз және оларды тиіп тұрған үшбұрыштардың центріне дейін жалғастырамыз. Егер біз әрбір үшбұрыш үшін осы центрден қалған екі бұрышқа дейін доғалар жүргізсек және оларды [тиіп тұрған] үшбұрыштардың центріне дейін жалғастырсақ, онда біз тең қабырғалы және тең бүйірлі үшбұрыш болатындай  сфераны теңдей төрт бөлікке бөлеміз: бұл үшбұрыштар IHF, IKH және FKH және  FIK60.  Міне оның суреті [172-сурет].

[172-сурет]

Есептің шешуі

Салу керек: сфераны өзара тең төрт сфералық дұрыс үшбұрыштарға бөлу.

Салу: әл Фәрәби әдісі бойынша салу (12сурет):

1) ABCD, BEDG және CEAG шеңберлерін жүргіземіз;

2) ABE, AED, ADG, AGB, СВЕ, CED, CDG және CGB дұрыс үшбұрыштарын саламыз;

3) төрт дұрыс үшбұрыштар: IHF, ІКН, FKH және FIK, мұндағы:

-  I, K, F нүктелері – ABCD, BEDG және CEAG шеңберлерінің сәйкесті центрлері;

- H – ABE сферасының центрі және және IKF сферасына тиісті.,

- HIKF – IKF сферасына іштей сызылған тетраэдр.

4) іштей сызылған тетраэдр төбелерін қос-қостан қосатын сфераның үлкен шеңберлерінің доғаларынан құралатын фигуралар – сфераны өзара тең төрт сфералық дұрыс үшбұрыштарға бөледі, яғни, ізделінді фигуралар.

 

 

 

 

 

 

 

 

 

 

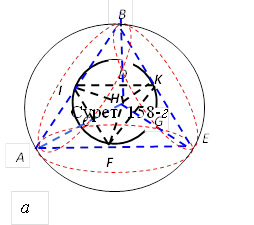
12-сурет. Трактаттағы № 158 сурет бойынша  а сызба

 

Ескертпе: әл Фәрәбидің «Рухани айлалы тәсілдер мен геометриялық фигуралардың табиғи сырлары туралы» кітабына А. Көбесовтың түсініктемелеріндегі № 60  ескертпе [1, б.: 230-231]: сфераға іштей сызылған дұрыс тетраэдр салуға келеді («Евклидтің бастамасындағы» XIII- кітаптың 13-сөйлемі ( III-том, беттер: 121-123)) [2, б.: -123].

«Евклидтің бастамасындағы» XIII-кітаптың 13-сөйлемі: сферамен қамтылған пирамида құрастыру және сфераның диаметрі шаршы бірлігінде пирамида қабырғасынан бір жарым есе үлкен болатыны көрсету: 13-сызба (13-суретте):

1) берілген сфераның AB – диаметрін өлшеп саламыз, оны C нүктесінде, AC кесіндісі CB-дан екі есе үлкен болатындай етіп бөлеміз;

 

I

 

 

 

 

 

 

 

 

 

 

 


 

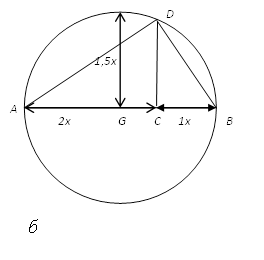
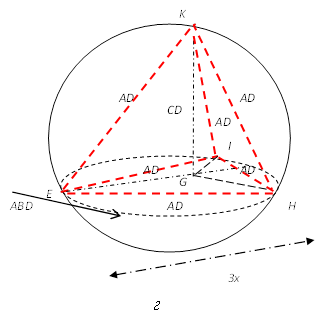
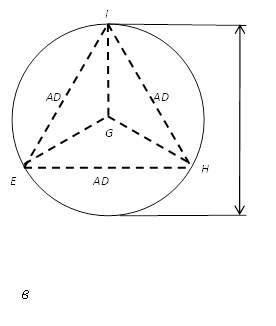
13-сурет. Евклид әдісімен сфераға іштей  тетраэдр салу

 

2) AB-ға сырттай тіркеп ADB жартыдөңгелек саламыз;

3) C нүктесінен AB-ға тікбұрыш жасап CD-ны саламыз;

4) DA кесіндісін жүргіземіз;

5) сфераның диаметрлік қимасын қарастырамыз – радиусы DC-ға тең EIH дөңгелегі;

6) EIH дөңгелегіне теңқабырғалы EIH үшбұрышын іштей сызамыз;

7) Дөңгелектің центрі – G нүктесін белгілейміз;

8) EG, GI, GH кесінділерін жүргіземіз;

9) G нүктесінен EIH жартыдөңгелегінің жазықтығына GK  перпендикулярын тұрғызамыз; 10)  GK-дан AC-ға тең GK кесіндісін қиып аламыз;

11) KE, EI, KH кесінділерін жүргіземіз;

12) EIH, KEI, KIH, KEH теңқабырғалы үшбұрыштары – ізделінді фигуралар; 13) теңқабырғалы төрт үшбұрыштан табаны EIH үшбұрышы болатын пирамида құрастырылады, оның төбесі  K – ол үшбұрыш қабырғаларынан бірдей қашықтықта, сфераның бетіне және EIH үшбұрышының жазықтығына перпендикулярға тиісті болады;

14) пирамидаға кез келген сфераны сырттай сызу ( сфера радиусы 1,5x-ке тең болады, себебі, диаметр AB=3х, мұндағы х=CB=1x  – өлшем бірлігі.

 

  [VІ] Тең қабырғалы және тең бұрышты үшбұрыш болатындай  сфераны теңдей төрт бөлікке бөлудің басқа [тәсілі]. Егер ол тең қабырғалы және тең бұрышты теңдей үш үшбұрыш болатындай  сфераны қалай теңдей төрт бөлікке бөлу керек десе, егер сфераның диаметрі белгілі болса, онда егер сфераның диаметрі AB сызығына тең болса, AB сызығында жарты дөңгелек тұрғызамыз да AB-ның үштен біріне тең  AB-ны белгілейміз,  AB-ға перпендикульяр  CD  сызығын жүргіземіз. Ол жарты дөңгелекпен D нүктесінде қилысады. дөңгелектен кез- келген Е нүктесін белгілеп, оны полюс  ретінде қабылдап BD-қашықтықта FGH дөңгелегін сызамыз да,  G, H, F нүктелерінде теңдей үш бөлікке бөлеміз және полюс пен G, H, F нүктелерінің әрқайсысы арқылы I нүктесінде қиылысатын  үлкен дөңгелектің доғаларын, ал  әрбір екі G, H және F нүктелері арқылы үлкен дөңгелек доғаларын  жүргіземіз. Сонда тең қабырғалы және тең бүйірлі үшбұрыш болатындай  теңдей төрт бөлікке бөлінген сфера аламыз. Бұл IHF, IHG, FIG және GHF61үшбұрыштары.  Міне оның суреті [173-сурет].

 

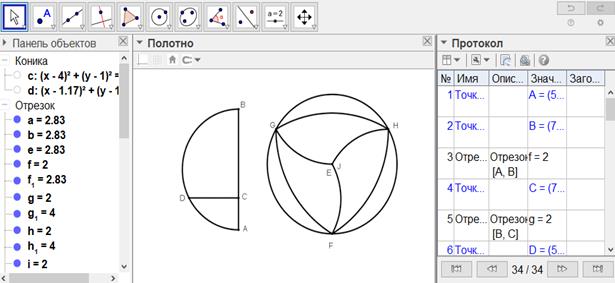
[173-сурет]

Есептің шешуі

Салу керек: сфераны өзара тең төрт сфералық дұрыс үшбұрыштарға бөлу.

Салу: әл Фәрәби әдісі бойынша салу (15-сурет):

1) сфераның диаметрі  AB кесіндісіне тең,

2) AВ кесіндісінде жартыдөңгелек саламыз,

3) AB-ның үштен біріне тең АС кесіндісін өлшеп саламыз, ;

4)  болатындай CD кесіндісін саламыз,

5)    , мұндағы  ADB – жартыдөңгелек;

6)  дөңгелекке тиісті,

 

 

 

 

 

 

 

 

 

 

 

 

 

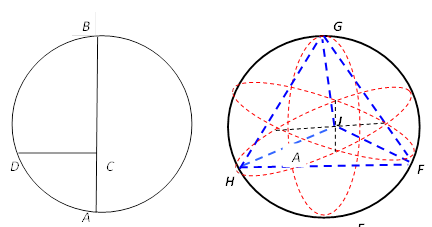
15-сурет. Трактаттағы № 159 сурет бойынша сызба

 

7) Шеңбер1(E, r=BD) | Шеңбер1=FGH,

8) Шеңбер1 -ді G, H, F нүктелерінде теңдей үш бөлікке бөлеміз;

9) берілген сфераның  J центрі арқылы, сондай-ақ G, H және F нүктелерінің әрбір жұбы арқылы үлкен шеңберлер жүргіземіз;

10) JHF, JHG, FJG және GHF төрт сфералық дұрыс үшбұрыштар – сфераның ізделінді фигурлары.

Ескертпе: әл Фәрәбидің «Рухани айлалы тәсілдер мен геометриялық фигуралардың табиғи сырлары туралы» кітабына А. Көбесовтың түсініктемелеріндегі № 61  ескертпе [1, б.: 231]: Шындығында жоғарыда айтылған «Евклидтің Бастамасындағы» 13 кітаптағы XIII  сөйлемге сәйкес келеді [3, б.:121-123].

 

  [VІІ] Тең қабырғалы және тең бұрышты төртбұрыш болатындай  сфераны теңдей алты бөлікке бөлу туралы. Егер біз осыны тұрғызғымыз келсе, онда тік бұрышпен қиылысатын үш үлкен дөңгелек тұрғызамыз. Ары қарай сферада өзіміз алған сегіз үшбұрыштың әрбір екеуінің ценрті арқылы үлкен дөңгелектер доғасын жүргіземіз. Сонда сфера тең қабырғалы және тең бүйірлі төртбұрыш болатындай  теңдей алты бөлікке бөлінеді және не салғымыз келсе, соны аламыз62. Міне оның суреті [174-сурет].

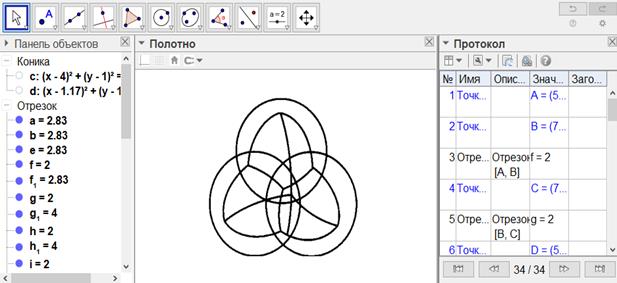
[174-сурет]

Есептің шешуі

Салу керек: сфераны алты сфералық дұрыс төртбұрыштарға бөлу.

Салу: әл Фәрәби әдісі бойынша салу (17-сурет):

1) осы сферамен шектелген шардың бір-бірімен тік бұрыш жасап қиылысатын үш үлкен дөңгелек жүргіземіз;

2) сферада алынған осы сегіз сфералық үшбұрыштардың  центрлерінің әрбір жұбы арқылы сфераның үлкен дөңгелектерін жүргіземіз;

3) Сонда сфера алты теңқабырғалы және теңбұрышты төртбұрыштарға бөлінеді, бұл – ізделінді фигуралар.

Ескертпе: әл Фәрәбидің «Рухани айлалы тәсілдер мен геометриялық фигуралардың табиғи сырлары туралы» кітабына А. Көбесовтың

түсініктемелеріндегі № 62  ескертпе [1, б.: 231]: Шындығында жоғарыда айтылған «Евклидтің Бастамасындағы» 15 кітаптағы XIII  сөйлемге сәйкес келеді [2, б.: 125-126].

Салу: Евклид әдісі бойынша сфераға іштей куб салу (18-сурет):

1) берілген сфераның AB – диаметрін бөліп аламыз да, оны C нүктесінде  AC кесіндісі CB-дан екі есе үлкен болатындай етіп бөлеміз;

2) AB-да  ADB жартыдөңгелегін жүргіземіз;

3) C нүктесінен AB-ға тік бұрыш жасап CD кесіндісін жүргіземіз;

4) DB кесіндісін жүргіземіз.

5) қабырғасы DB-ға тең болатын EIHG квадратты қарастырамыз;

6) квадраттың төбелерінен  квадрат жазықтығына перпендикулярлар жүргізіп,  DB-ға тең кесінділер өлшеп саламыз;

7) куб саламыз (19-сурет).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

17-сурет. Трактаттағы № 150 сурет бойынша сызба

 

Математикалық негіздеу: сферның радиусы 1,5x-ге тең, себебі диаметр AB=3х, мұндағы: х=CB=1x  – өлшем бірлік. Евлид әдісі арқылы салынған куб қабырғаларының теңдігі бойынша куб төбелері сфера бетінде бір-бірінен тең арақашықтықта орналасады, ендеше, олардың жұбы арқылы жүргізілген сфераның үлкен шеңберінің доғалары да өзара тең болады. Бұдан сфераның алты сфералық дұрыс төртбұрыштарға бөлінетіндігі шығады, яғни бұл – ізделінді фигуралар. Дәлелдеу керегі осы.

 

 

 

 

 

 

 

 

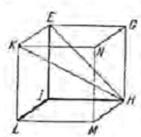
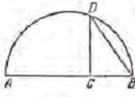
18-сурет. Еклид бойынша сызба

 

 

 

 

 

 

 

 

 

 

19-сурет. Іштей сызылған куб

 

VII-ші есепте келтірілген Евклид есебінің шарты әл Фараби есебінің шартынан айырмашылығы бар. Әл Фараби сфераның бетін теңдей алты бөлікке бөлуді, ал Евкид сфераға іштей куб салуды қарастырады: «Сферамен көмкерілген пирамида сияқты, куб салу және сфераның кубтан шаршы бірлікте үш есе үлкен екендігін көрсету». Дегенмен, әл Фәрәби сфераны теңдей алтыға бөлуде Евклидтің осы әдісін қолданады. Бұл жөнінде А. Көбесовтың ескертпесі жағарыда келтірілген.

 

  [VIII] Сфераны тең қабырғалы және тең бұрышты алты төртбұрышқа бөлудің келесі бір әдісі. Егер ол сфераны қалай тең қабырғалы және тең бұрышты алты төртбұрышқа бөлуге болады десе, егер сфераның диаметрі АВ кесіндісіне тең болса, онда АВ кесіндісі бойынан жарты дөңгелек сызамыз, АВ-ның үштен біріне тең болатын АС-ны белгілейміз, С нүктесінен АС ға перпендикуляр СD-ны тұрғызып, А мен D нүктелерін қосамыз, сфераға Е және G нүктелерінде тік бұрышпен қиылысатын екі дөңгелекті саламыз, әрбір Е және G нүктелерін полюс ретінде қабылдап АD қашықтықта H, F, I, К, L, Μ, Ν және X нүктелерін белгілейміз, осы нүктелердің әрқайсысынан үлкен дөңгелек жүргіземіз, яғни төрт доға H, F, I және К нүктелерінің және L, Μ, Ν, X нүктелерінен арасынан жүргіземіз.

Сонда сфера алты тең қабырғалы және тең бұрышты төртбұрышқа бөлінеді63. Міне оның суреті [175-сурет].

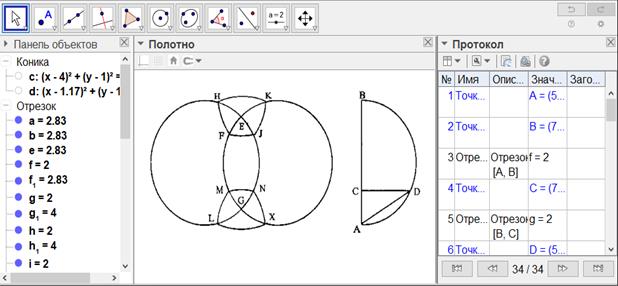
[175-сурет]

Есептің шешуі

Салу керек: сфераны алты сфералық дұрыс төртбұрыштарға бөлу.

Салу: әл Фәрәби әдісі бойынша салу (17-сурет):

1) осы сферамен шектелген шардың бір-бірімен тік бұрыш жасап қиылысатын үш үлкен дөңгелек жүргіземіз;

2) сферада алынған осы сегіз сфералық үшбұрыштардың  центрлерінің әрбір жұбы арқылы сфераның үлкен дөңгелектерін жүргіземіз;

3) Сонда сфера алты теңқабырғалы және теңбұрышты төртбұрыштарға бөлінеді, бұл – ізделінді фигуралар.

Ескертпе: әл Фәрәбидің «Рухани айлалы тәсілдер мен геометриялық фигуралардың табиғи сырлары туралы» кітабына А. Көбесовтың

түсініктемелеріндегі № 62  ескертпе [1, б.: 231]: Шындығында жоғарыда айтылған «Евклидтің Бастамасындағы» 15 кітаптағы XIII  сөйлемге сәйкес келеді [2, б.: 125-126].

Салу: Евклид әдісі бойынша сфераға іштей куб салу (18-сурет):

1) берілген сфераның AB – диаметрін бөліп аламыз да, оны C нүктесінде  AC кесіндісі CB-дан екі есе үлкен болатындай етіп бөлеміз;

2) AB-да  ADB жартыдөңгелегін жүргіземіз;

3) C нүктесінен AB-ға тік бұрыш жасап CD кесіндісін жүргіземіз;

4) DB кесіндісін жүргіземіз.

5) қабырғасы DB-ға тең болатын EIHG квадратты қарастырамыз;

6) квадраттың төбелерінен  квадрат жазықтығына перпендикулярлар жүргізіп,  DB-ға тең кесінділер өлшеп саламыз;

7) куб саламыз (19-сурет).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

17-сурет. Трактаттағы № 150 сурет бойынша сызба

 

Математикалық негіздеу: сферның радиусы 1,5x-ге тең, себебі диаметр AB=3х, мұндағы: х=CB=1x  – өлшем бірлік. Евлид әдісі арқылы салынған куб қабырғаларының теңдігі бойынша куб төбелері сфера бетінде бір-бірінен тең арақашықтықта орналасады, ендеше, олардың жұбы арқылы жүргізілген сфераның үлкен шеңберінің доғалары да өзара тең болады. Бұдан сфераның алты сфералық дұрыс төртбұрыштарға бөлінетіндігі шығады, яғни бұл – ізделінді фигуралар. Дәлелдеу керегі осы.

 

 

 

 

 

 

 

 

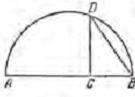
18-сурет. Еклид бойынша сызба

 

 

 

 

 

 

 

 

 

 

19-сурет. Іштей сызылған куб

 

VII-ші есепте келтірілген Евклид есебінің шарты әл Фараби есебінің шартынан айырмашылығы бар. Әл Фараби сфераның бетін теңдей алты бөлікке бөлуді, ал Евкид сфераға іштей куб салуды қарастырады: «Сферамен көмкерілген пирамида сияқты, куб салу және сфераның кубтан шаршы бірлікте үш есе үлкен екендігін көрсету». Дегенмен, әл Фәрәби сфераны теңдей алтыға бөлуде Евклидтің осы әдісін қолданады. Бұл жөнінде А. Көбесовтың ескертпесі жағарыда келтірілген.

«[VIII] Сфераны алты теңқабырғалы және теңбұрышты төртбұрыштарға бөлудің басқа тәсілі. Егер ол, сфераны алты теңқабырғалы және теңбұрышты төртбұрыштарға қалай бөлу керек десе, сфераның диаметрін AB сызығына тең деп алып, AB-да жартыдөңгелек саламыз. AB-ның үштен біріне тең  АС-ны саламыз,  С нүктесінен АС-ға перпендикуляр CD  сызығын тұрғызамыз және А мен D-ні қосамыз, сферада Е және G нүктелерінде тік бұрыш жасап қиылысатын екі дөңгелек жүргіземіз, Е және G нүктелерінің әрқайсысын полюс етіп аламыз және AD қащықтықта H, F, I, К, L, Μ, Ν және X нүктелерін белгілейміз, осы нүктелердің әрқайсысы арқылы үлкен дөңгелектің доғаларын жүргіземіз, яғни H, F, I және К нүктелерінің арасындағы доғаларды саламыз. Сонда, сфера алты теңқабырғалы және теңбұрышты төртбұрыштарға бөлінеді. Міне оның суреті: 161-сурет (20-суретте) [1, б: 212-213]».

 

 

 

 

 

 

 

 

 

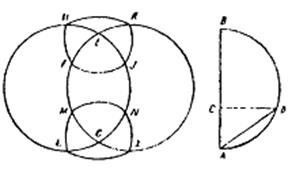
20-сурет. Трактаттағы № 161 сурет

 

Есептің шешуі

Салу керек: сфераны алты теңқабырғалы және теңбұрышты сфералық төртбұрыштарға бөлудің басқа тәсілін көрсету.

Ескертпе: әл Фәрәбидің «Рухани айлалы тәсілдер мен геометриялық фигуралардың табиғи сырлары туралы» кітабына А. Көбесовтың түсініктемелеріндегі № 63 ескертпе [1, б.: 231]: шындығында жоғарыда айтылған «Евклидтің Бастамасындағы» 15 кітаптағы XIII  сөйлемге сәйкес келеді [2, c.: 125-126]. Жоғарыда келтірілген 7-ші есептегі Евклид әдісін қараңыз.

 

  [ІХ] Тең қабырғалы және тең бұрышты үшбұрыш болатындай  сфераны теңдей жиырма бөлікке бөлу туралы. Егер ол тең қабырғалы және тең бұрышты үшбұрыш болатындай сфераны қалай теңдей жиырма бөлікке бөлуге болады десе, онда полюсы H және G нүктелері болатын сферада үлкен ABCD дөңгелегін тұрғызамыз. Бұл дөңгелекті теңдей он бөлікке бөлеміз; Бұл бөліктер AB, BC, CD, DE, EF, FI, IK, KL, LM  және MA. A және B нүктелерін полюс терінде қабылдап, BC доғасы қашықтығында Н жағында Z нүктесінде қиылысатын екі дөңгелек сызамыз. Содан соң B және C нүктелерін полюс терінде қабылдап, BC доғасы қашықтығында Q жағында G нүктесінде қиылысатын екі дөңгелек сызамыз. Үлкен дөңгелектің он бөлігінің әрбірінде, он бөлікке бөлінген,   Н жағында Z нүктесінде және G жағында Q нүктесінде қиылысатын дөңгелектер сызамыз. Бізде Z-пен белгіленетін Н полюсі жағынан бес нүкте және Q-мен белгіленетін Н полюсі жағынан бес нүкте пайда болады. Осы нүктелердің әрбір екеуін, яғни Z және Q-ді үлкен дөңгелектің доғаларымен қосамыз. Төбелері Z және Q болатын, ал табандары  QQ және ZZ сызықтары болатын он үшбұрыш пайда болады. Ары қарай әрбір Z нүктесі мен H полюсі және әрбір Q нүктесі мен G полюсі арқылы үлкен дөңгелек доғаларын жүргіземіз. Төбелері H нүктесінде болатын бес үшбұрыш және төбелері G нүктесінде болатын бес үшбұрыш пайда болады. Осындай әдіспен сфераны теңдей тең қабырғалы және тең бұрышты жиырма үшбұрышқа бөлеміз64. Міне оның суреті [176-сурет].

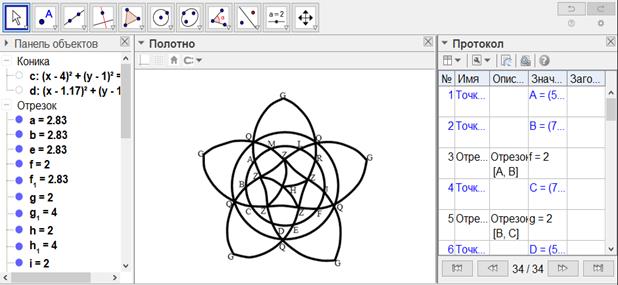
[176-сурет]

Есептің шешуі

Салу керек: сфераны жиырма сфералық дұрыс  үшбұрыштар болып табылатын тең бөліктерге бөлу.

Салу: әл Фәрәби әдісі бойынша салу (22-сурет):

1.Сфераның ABCD үлкен шеңберін жүргіземіз, ал оның полюстері (диаметрінің шеткі нүктелері) – H және G нүктелері:

2. Осы шеңберді теңдей он  бөліктерге бөлеміз; бұл бөліктер: AB, ВС, CD, DE, EF, FI, IK, KL, LM және MA;

3. А және В нүктелерін полюстер етіп аламыз және  ВС доғасына дейінгі қашықтықта, H  полюсы жағынан Z нүктесінде қиылысатын екі шеңбер жүргіземіз;

4. B және C нүктелерін полюстер етіп аламыз және  ВС доғасына дейінгі қашықтықта, G полюсы жағынан Q нүктесінде қиылысатын екі шеңбер жүргіземіз;

5. Он бөлікке бөлінген үлкен шеңбердің әр он бөлігінен H нүктесі жағынан Ζ нүктесінде және  G полюсі жағынан Q нүктесінде қиылысатын дөңгелектер жүргіземіз;

22-сурет. Трактаттағы № 162 сурет бойынша сызба

 

6. Бізде Z-пен белгіленетін Н полюсі жағынан бес нүкте және Q-мен белгіленетін G полюсі жағынан бес нүкте пайда болады;

7. Осы нүктелердің әрбір екеуін, яғни Z және Q нүктелерін үлкен шеңбердің доғаларымен қосамыз;

8. Біз  Ζ және Q нүктелері – төбелері, ал табандары – QQ және ΖΖ  сызықтары болып табылатын он сфералық үшбұрыш пайда болады;

9. Н полюсі мен Z нүктелерінің әрқайсысы арқылы және G полюсы мен Q нүктелерінің әрқайсысы арқылы үлкен шеңбердің доғаларын жүргіземіз;

10. Төбелері H нүктесінде жататын бес сфералық үшбұрыш және төбелері G нүктесінде жататын бес сфералық үшбұрыш пайда болады;

11. сфераның бетінде жатқан осы өзара тең жиырма сфералық дұрыс үшбұрыштар – ізделінді фигуралар.

Ескертпе: әл Фәрәбидің «Рухани айлалы тәсілдер мен геометриялық фигуралардың табиғи сырлары туралы» кітабына А. Көбесовтың түсініктемелеріндегі № 64  [1, б.: 213-214]: «Евклидтің Бастамасындағы» 13 кітаптың XIII  сөйлеміне сәйкес келеді (т.III, бет: 127);  [2, б.; 127-131]) (келесі 10-есептен қараңыз).

 

  [Х] Осы салудың басқа әдісі. Егер біз тең қабырғалы және тең бұрышты үшбұрыш болатындай  сфераны теңдей жиырма бөлікке бөлгіміз келсе және сфераның диаметрі AB сызығына тең болса, онда AB сызығының бойында ABC жарты дөңгелегін тұрғызамыз, AB-ның бестен біріне тең BD-ны белгілейміз, DB сызығына перпендикуляр DC тұрғызамыз,  B нүктесін центр ретінде қабылдаймыз және BC қашықтықта CEG дөңгелегін саламыз. CEG дөңгелегінің бестен біріне тең CE доғасын белгілейміз. Сферада кез келген H нүктесін белгілеп, оны полюс ретінде қабылдаймыз және CE қашықтықта сферада дөңгелек тұрғызамыз. Дөңгелекті F нүктесінде теңдей бес бөлікке бөлеміз, әрбір екі осындай нүктелер арқылы үлкен дөңгелек доғаларын жүргіземіз және  әрбір осы нүктелер мен полюс арқылы дәл сондай үлкен дөңгелек доғаларын жүргіземіз. Сферада төбелері H нүктесінде және табандары FF болатын тең қабырғалы және тең бұрышты бес үшбұрыш аламыз. Ары қарай F нүктесінің әрбірін полюс ретінде аламыз және I нүктесінде қиылысатын, алынған қашықтықта дөңгелектер тұрғызамыз.  Содан соң әрбір екі F нүктесі және әрбір екі I нүктесі арқылы үлкен дөңгелек доғаларын жүргіземіз. Сонда тең қабырғалы және тең бұрышты он үшбұрыш аламыз. Содан соң әрбір екі I нүктесін полюс ретінде аламыз және сондай қашықтықта K нүктесінде қиылысатын дөңгелектер сызамыз. Содан соң әрбір I нүктесіне және әрбір K нүктесіне үлкен дөңгелек доғаларын тұрғызамыз. Сонда тең қабырғалы және тең бұрышты бес үшбұрыш аламыз. Сәйкесінше, сфераның жоғарғы бетін тең қабырғалы және тең бұрышты үшбұрыш болатындай жиырма бөлікке бөлеміз65.  Міне оның суреті [177- сурет].

 

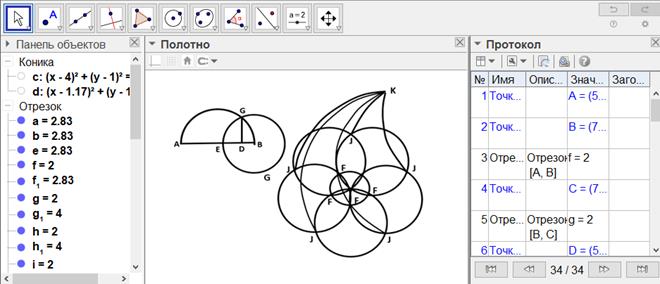
[177-сурет]

Есептің шешуі

Салу керек: сфераны жиырма  сфералық дұрыс үшбұрыштар болып табылатын өзара тең бөліктерге бөлу немесе сфераның саны 20-ға тең триангуляциясы.

Ескертпе: әл Фәрәбидің «Рухани айлалы тәсілдер мен геометриялық фигуралардың табиғи сырлары туралы» кітабына А. Көбесовтың түсініктемелеріндегі № 65  ескертпе [1, б.: 230-231]: аталған «Евклидтің Бастамасындағы»  VI  кітаптың XVI  сөйлеміне сәйкес келеді [2, б.: 127-131]. Суретте қателік бар.

 

 

 

 

 

 

 

 

 

 

 

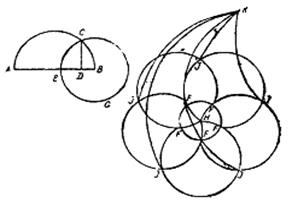
23-сурет. Трактаттағы № 163 сурет

 

Салу: Евклид бойынша сфераға іштей икосаэдр салу (24-сурет).

1) берілген сфераның  AB – диаметрін өлшеп саламыз. Оны C нүктесінде AC кесіндісі CB-дан төрт есе үлкен болатындай етіп, бөлеміз;

2) AB-да  ADB жартыдөңгелегін саламыз;

3) C нүктесінен CD кесіндісін AB-ға тік бұрыш жасап жүргіземіз;

4) DB кесіндсін жүргіземіз;

5) радиусы DB-ға тең EJHGK шеңберін жүргіземіз де, осы шеңберге іштей  дұрыс бесбұрыш саламыз;

6) EJ, JH, HG, GK, KE қисықтарын L, M, N, Q, O нүктелерінде қақ бөлеміз;

7) LM, MN, NQ, QO, OL, LO кесінділерін жүргіземіз;

8) LMNQO –дұрыс бесбұрыш;

9) EO кесіндісі –дұрыс онбұрыштың қабырғасы;

10) E, J, H, Q, K нүктелерінде дөңгелек жазықтығына перпендикулярлар тұрғызамыз;

11) EP, JR, HS, GT, KU кесінділері EJHGK дөңгелегінің центрінен бірдей қашықтықта орналасқан;

12) PR, RS, ST, TU, UP кесінділерін жүргіземіз, сондай-ақ  PL, LR, RM, MS, SN, NT, TQ, QU, UO, OP кесінділерін жүргіземіз.

 

 

 

 

 

 

 

 

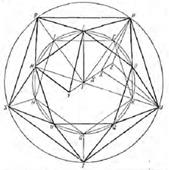
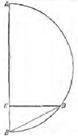
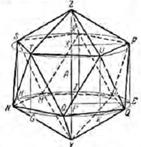
24-сурет. Евклидтің «Бастамасындағы» № 17-сызба

 

12) EP, KU кесінділерінің әрқайсысы бір ғана жазықтыққа перпендикуляр, ендеше: EP||KU және  EP= KU;

13)  PU=EK; PU||EK;

14) бірақ EK – дұрыс бесбұрыштың қабырғасы, ендеше:  PU – кесіндісі

EJHGK дөңгедегіне іштей сызылған дұрыс бесбұрыштың қабырғасы;

15) икосаэдр саламыз (25-сурет):

а) EJHGK және PRSTU шеңберлерінің центрлері арқылы өтетін FX түзуін   жүргіземіз;

б) FX-тің ортасы – A нүктесін табамыз, бұл – радиусы AE болатын шеңбердің центрі;

в) сфераның FX осімен қиылысу нүктелерін: X және Y арқылы белгілейміз;

д) X нүктесін P, R, S, T, U нүктелерінің әрқайсысымен,, ал Y нүктесін : E, J, H, G, K нүктелерінің әрқайсысымен кесінділер арқылы қосамыз;

16) сонда осы іштей салынған икосаэдрдің төбелері арқылы сфераның беті ізделінді жиырма сфералық дұрыс  үшбұрыштарға бөлінеді (26-сурет):  – (мұндағы, сфераның  радиусы: 2,5x, себебі: диаметр AB=5х, мұнда: х=CB=1x  – өлшем бірлік.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

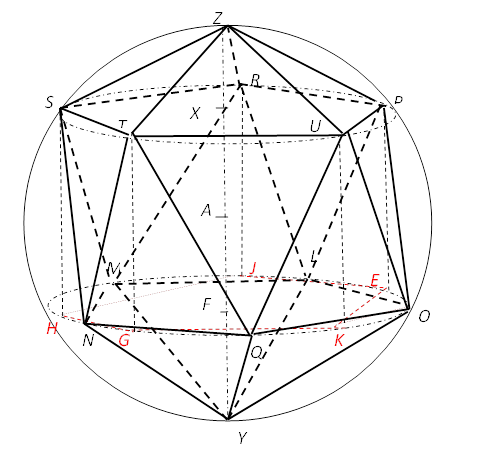
25-сурет. Трактаттағы № 163 сурет бойынша сызба

 

Осылай, X-есебінде әл Фәрәби грек геометрі Евклидтің сфераға икосаэдрді іштей салу әдісін пайдаланып, сфераның бетін жиырма сфералық дұрыс үшбұрыштарға бөлуді іске асыру әдісін ұсынған. Евклид есебінің шарты әл Фәрәби есебінің шартынан өзгеше, ол: «Икосаэдр құрастырамыз, оны жоғарыда көрсетілген фигуралар сияқты сферамен көмкереміз және мұнда икосаэдрдің қабырғасы иррационал болады – яғни, «кіші» (жуық) дейтін түрде болады», деп жазған [2, б.: 127-131].

Математикалық негіздеу: Шыныменен: ZSNYOP – тең бүйірлі алтыбұрыш, ал PLSTU = EJHGK – тең бүйірлі бесбұрыш. Алтыбұрыш пен бесбұрыш радиустары әртүрлі шеңберлерге іштей сызылған. Ендеше: SN=NT=TQ=QU=UO=OP=PL=LR=RM=MS – алтыбұрыштың қабырғалары, ал ST=TU=UP=PR=RS =NQ=QO=OL=LM=MN – бесбұрыштың қабырғалары. Бұдан осы геометриялық денені құрастырып тұрған үшбұрыштардың – теңқабырғалы емес, теңбүйірлі екендіктері шығады.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


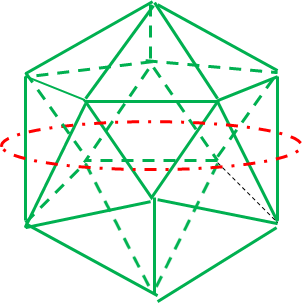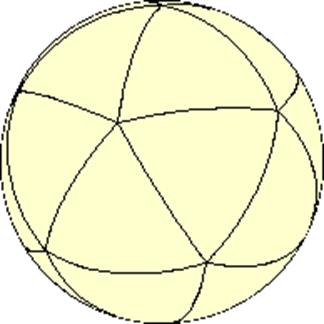
Описание: http://wiki.gis-lab.info/images/6/63/Sph_icosahedron.png

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

26-сурет. Сфераның саны  жиырма болатын сфералық триангуляциясы

Ендеше «икосаэдрдің» қабырғалары жуық түрде тең болады. Сонымен бірге келесі лемманы ескеру қажет: рационал диаметрі бар шеңберге, теңқабырғалы бесбұрыш іштей сызылса, оның қабырғалары иррационал (Евклид бойынша: «кіші») болады. Дәлелдеу керегі осы.